Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T23:59:06.545Z Has data issue: false hasContentIssue false
  • English
  • Français

Modular descent of Siegel modular forms of half integral weight and an analogy of the Maass relation

Published online by Cambridge University Press:  22 January 2016

Yoshio Tanigawa
Yoshio Tanigawa*
Affiliation:
Department of Mathematics, Faculty of Science, Nagoya University, Chikusa-ku, Nagoya 464, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [8], H. Maass introduced the ‘Spezialschar’ which is now called the Maass space. It is defined by the relation of the Fourier coefficients of modular forms as follows. Let f be a Siegel modular form on Sp(2,Z) of weight k, and let 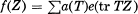be its Fourier expansion, where 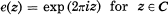. Then f belongs to the Maass space if and only if

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 102 , June 1986 , pp. 51 - 77
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1986

References

[ 1 ] Andrianov, A. N., Modular descent and the Saito-Kurokawa conjecture, Invent. Math., 53 (1979), 267–280.Google Scholar
[ 2 ] Eichler, M. and Zagier, D., The theory of Jacobi forms, Progress in Mathematics, 55, Birkhäuser, 1985.Google Scholar
[ 3 ] Hayakawa, S., On Hecke operators of Siegel modular forms of half integral weight, preprint.Google Scholar
[ 4 ] Hina, T., On Siegel modular forms of second degree which has half integral weight, (in Japanese), preprint.Google Scholar
[ 5 ] Ibukiyama, T., On construction of half integral weight Siegel modular forms of Sp(2, R) from automorphic forms of the compact twist Sp(2), MPI/SFB 84–18.Google Scholar
[ 6 ] Igusa, J., Theta Functions, Die Grundlehren der Mathematischen Wissenschaften in Einzeldarstellungen, 194, Springer-Verlag, Berlin 1972.Google Scholar
[ 7 ] Kitaoka, Y., A note on local densities of quadratic forms, Nagoya Math. J., 92 (1983), 145–152.Google Scholar
[ 8 ] Maass, H., Über eine Spezialschar von Modulformen zweiten Grades, Invent. Math., 52 (1979), 95–104.Google Scholar
[ 9 ] Maass, H., über eine Spezialschar von Modulformen zweiten Grades II, Invent. Math., 53(1979), 249–253.Google Scholar
[10] Maass, H., Über eine Spezialschar von Modulformen zweiten Grades III, Invent. Math., 53 (1979), 255–265.Google Scholar
[11] O’Meara, O. T., Introduction to quadratic forms, Die Grundlehren der Mathematischen Wissenschaften in Einzeldarstellungen, 117, Springer-Verlag 1963.Google Scholar
[12] Shimura, G., On modular forms of half integral weight, Ann. of Math., 97 (1973), 440–481.Google Scholar
[13] Zagier, D., Sur la conjecture de Saito-Kurokawa (d’apres H. Maass), Seminaire Delange-Pisot-Poitou, 1979–1980, in Progress in Math. 12, Birkhäuser-Verlag, 1980, 371–394.Google Scholar