Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-05T06:56:28.518Z Has data issue: false hasContentIssue false
  • English
  • Français

Lp-curvature and the Cauchy-Riemann equation near an isolated singular point

Published online by Cambridge University Press:  22 January 2016

Adam Harris  and
Yoshihiro Tonegawa
Adam Harris
Affiliation:
School of Mathematics and Statistics, University of Melbourne, Parkville, VIC 3052, Australia, [email protected]
Yoshihiro Tonegawa
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo 060-0810, Japan, tonegawa@@math.sci.hokudai.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a complex n-dimensional reduced analytic space with isolated singular point x0, and with a strongly plurisubharmonic function ρ : X → [0, ∞) such that ρ(x0) = 0. A smooth Kähler form on X \ {x0} is then defined by i∂∂ρ. The associated metric is assumed to have 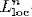-curvature, to admit the Sobolev inequality and to have suitable volume growth near x0. Let E → X \ {x0} be a Hermitian-holomorphic vector bundle, and ξ a smooth (0, 1)-form with coefficients in E. The main result of this article states that if ξ and the curvature of E are both 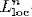then the equation 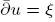has a smooth solution on a punctured neighbourhood of x0. Applications of this theorem to problems of holomorphic extension, and in particular a result of Kohn-Rossi type for sections over a CR-hypersurface, are discussed in the final section.

Keywords

32D2032L10
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 164 , December 2001 , pp. 35 - 51
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2001

References

[1] Andreotti, A. and Vesentini, E., Carleman estimates for the Laplace-Beltrami equation on complex manifolds, Publ. Math. I.H.E.S., 25 (1965), 81-130.CrossRefGoogle Scholar
[2] Bando, S., Removable singularities for holomorphic vector bundles, Tohoku Math. J., 43 (1991), 61-67.CrossRefGoogle Scholar
[3] Bando, S., Kasue, S. and Nakajima, H., On a construction of coordinates at infinity on manifolds with fast curvature decay and maximal volume growth, Invent. Math., 97 (1989), 313-349.CrossRefGoogle Scholar
[4] Buchdahl, N.P. and Harris, A., Holomorphic connections and extension of complex vector bundles, Math. Nachr., 204 (1999), 29-39.Google Scholar
[5] Dimca, A., Singularities and topology of hypersurfaces, Springer Universitext, 1992.CrossRefGoogle Scholar
[6] Federer, H., Geometric measure theory, Grund. Math. Wiss. Bd 153, Springer Berlin, Heidelberg, New York, 1969.Google Scholar
[7] Goresky, R.M. and MacPherson, R.P., Intersection homology theory, Topology, 19 (1980), 135-162.Google Scholar
[8] Grauert, H., Characterisierung der Holomorphiegebiete durch die vollstäntige Kählerische Metrik, Math. Ann., 131 (1956), 38-75.Google Scholar
[9] Harris, A. and Tonegawa, Y., Analytic continuation of vector bundles with Lp- curvature, Int. J. Math., 11, No.1 (2000), 29-40.CrossRefGoogle Scholar
[10] Hömander, L., L 2 - estimates and existence theorems for the -operator, Acta Math., 113 (1965), 89-152.CrossRefGoogle Scholar
[11] Kohn, J. and Folland, G., The Neumann problem for the Cauchy-Riemann complex, Ann. Math. Stud. 75, Princeton, 1972.Google Scholar
[12] Kohn, J. and Rossi, H., On the extension of holomorphic functions from the boundary of a complex manifold, Ann. Math., 81 (1965), 451-472.Google Scholar
[13] Laufer, H.B., On CP1 as an exceptional set, in “Recent developments in several complex variables” (J.E. Fornaess, Ed.) Ann. Math. Stud., Princeton 1981.Google Scholar
[14] Ohsawa, T., Cheeger-Goresky-MacPherson’s conjecture for varieties with isolated singularities, Math. Z., 206 (1991), 219-224.CrossRefGoogle Scholar
[15] Ohsawa, T., On the L2-cohomology groups of isolated singularities, Adv. Stud. Pure Math., 22 (1993), 247-263.Google Scholar
[16] Saper, L., L2 - cohomology of Kähler varieties with isolated singularities, J. Differential Geom., 36, No.1 (1992), 89-161.CrossRefGoogle Scholar