Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Khidr, Shaban
2019.
Holomorphic Approximation on Certain Weakly Pseudoconvex Domains in Cn.
Mathematics,
Vol. 7,
Issue. 11,
p.
1035.
Khidr, Shaban
2022.
Nonlinear Analysis, Geometry and Applications.
p.
407.


 on a certain pseudoconvex domain in ℂ
on a certain pseudoconvex domain in ℂ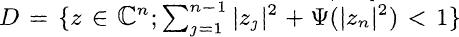 is a pseudoconvex domain with
is a pseudoconvex domain with 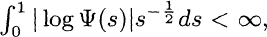 then we can obtain
then we can obtain 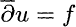 on
on 