Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T23:08:36.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower bounds for fundamental units of real quadratic fields

Published online by Cambridge University Press:  22 January 2016

Koshi Tomita  and
Kouji Yamamuro
Koshi Tomita
Affiliation:
Department of Mathematics, Meijo University, Shiogamaguchi 1-501, Tenpaku-ku, Nagoya, 468-8502, Japan, [email protected]
Kouji Yamamuro
Affiliation:
Department of Liberal Arts, Aichi Konan College, Omatsubara 172, Takaya-cho, Konan-shi, Aichi, 483-8086, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let d be a square-free positive integer and l(d) be the period length of the simple continued fraction expansion of ωd, where ωd is integral basis of ℤ[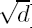]. Let εd = (td + ud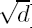)/2 (> 1) be the fundamental unit of the real quadratic field ℚ(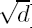). In this paper new lower bounds for εd, td, and ud are described in terms of l(d). The lower bounds of εd are sharper than the known bounds and those of td and ud have been yet unknown. In order to show the strength of the method of the proof, some interesting examples of d are given for which εd and Yokoi’s d-invariants are determined explicitly in relation to continued fractions of the form .

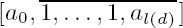Keywords

11R1111R27
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 166 , June 2002 , pp. 29 - 37
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2002

References

[1] Mollin, R. A., Quadratics, CRC Press, Boca Rato, FL., 1996.Google Scholar
[2] Sasaki, R., A characterization of certain real quadratic fields, Proc. Japan Acad., 62, Ser. A (1986), no. 3, 97–100.Google Scholar
[3] Tomita, K., Explicit representation of fundamental units of some quadratic fields, Proc. Japan Acad., 71, Ser. A (1995), no. 2, 41–43.Google Scholar
[4] Williams, K. S. and Buck, N., Comparison of the lengths of the continued fractions of and , Proc. Amer. Math. Soc., 120 (1994), no. 4, 995–1002.Google Scholar
[5] Yokoi, H., The fundamental unit and class number one problem of real quadratic fields with prime discriminant, Nagoya Math. J., 120 (1990), 51–59.Google Scholar
[6] Yokoi, H., a note on class number one problem for real quadratic fields, Proc. Japan Acad., 69, Ser. A (1993), 22–26.Google Scholar
[7] Yokoi, H., The fundamental unit and bounds for class numbers of real quadratic fields, Nagoya Math. J., 124 (1991), 181–197.CrossRefGoogle Scholar
[8] Yokoi, H., New invariants and class number problem in real quadratic fields, Nagoya Math. J., 132 (1993), 175–197.CrossRefGoogle Scholar