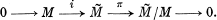Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T23:50:41.343Z Has data issue: false hasContentIssue false
  • English
  • Français

Long Exact Sequences and the Transgression Relation

Published online by Cambridge University Press:  22 January 2016

A. Berkson  and
Alan McConnell
A. Berkson
Affiliation:
University of Illinois, Howard University
Alan McConnell
Affiliation:
University of Illinois, Howard University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout what follows, let H be a normal subgroup of the group G, 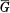be G/H, M a left G module, and HomH(G,M) = a left G module via (τϕ(σ) = (ϕ(στ)

In [1] the present authors compared the 5-term Hochschild Serre sequence to the long exact sequence arising from the short exact

sequence of modules

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 49 , March 1973 , pp. 67 - 75
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1973

References

[1] Berkson, A. J. and McConnell, Alan, On inflation-restriction exact sequences in group and Amitsur cohomology, Trans. Amer. Math. Soc, 141 (1969), 403–413.Google Scholar
[2] Childs, L. N., The exact sequence of low degree and normal algebras, Bull. Amer. Math. Soc, 76 (1970), 1121–1124.Google Scholar
[3] Hochschild, G. and Serre, J.-P., Cohomology of group extensions, Trans. Amer. Math. Soc, 74 (1953), 110–134.Google Scholar
[4] Pareigis, B. and Rosenberg, A., Adendum to “Amitsur’s complex for inseparable fields,” Osaka J. Math., 1 (1964), 33–44.Google Scholar
[5] Ribes, L., On a cohomology theory for pairs of groups, Proc. Amer. Math. Soc, 21 (1969), 230–234.Google Scholar
[6] Serre, J.-P., Corps Locaux, Hermann, Paris, 1962.Google Scholar