Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-11T12:26:52.082Z Has data issue: false hasContentIssue false
  • English
  • Français

Local times of self-intersection for multidimensional Brownian motion*

Published online by Cambridge University Press:  22 January 2016

Sheng-Wu He ,
Wen-Qiang Yang ,
Rong-Qin Yao  and
Jia-Gang Wang
Sheng-Wu He
Affiliation:
Department of Mathematical Statistics, East China Normal University, Shanghai 200062China
Wen-Qiang Yang
Affiliation:
Department of Mathematical Statistics, East China Normal University, Shanghai 200062China
Rong-Qin Yao
Affiliation:
Department of Mathematical Statistics, East China Normal University, Shanghai 200062China
Jia-Gang Wang
Affiliation:
Institute of Applied Mathematics, East China University of Technology, Shanghai 200237China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

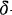We will define local times of self-intersection for multidimensional Brownian motion as generalized Wiener functionals under the framework of white noise analysis as in H. Watanabe ([6]). By making use of the chaotic representation of -function and precise computation we get a deep insight into the problem. In the section 1 multiple Wiener integrals with respect to multidimensional Brownian motion and chaotic representations for square-integrable Wiener functionals are given. They are indispensable, but seem not to be formulated clearly and correctly before. The useful concepts and results of white noise analysis are illustrated in the section 2. Section 3 is the main part of the paper. The applications to local times are introduced in the section 4 briefly.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 138 , June 1995 , pp. 51 - 64
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

Footnotes

*

The project supported by National Natural Science Foundation of China.

References

[ 1 ] Hida, T., Analysis of Brownian Functional, Carleton Math. Lecture, 13, 1975.Google Scholar
[ 2 ] Hida, T. and Potthoff, J., White noise analysis—an overview, In Hida, T. et al. (eds.) White Noise Analysis-Mathematics and Applications, World Scientific, Singapore, 1990.Google Scholar
[ 3 ] Ito, K., Multiple Wiener integrals, J. Math. Soc, Japan, 3 (1951), 157–169.Google Scholar
[ 4 ] Kubo, I, Ito formula for generalized Brownian functionals, Lecture Notes in Control and Information Science, No. 49 (1983), 156–166, Springer-Verlag.Google Scholar
[ 5 ] Potthoff, J. and Streit, L., A characterization on Hida distributions, J. Funct. Anal., 101 (1991), 212–229.Google Scholar
[ 6 ] Watanabe, H., The local time of self-intersections of Brownian motion as generalized Brownian functionals, Lett. Math. Phys., 23 (1991), 1–9.Google Scholar