No CrossRef data available.
Published online by Cambridge University Press: 20 January 2025
Let 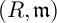 $(R,\mathfrak {m})$ be a Noetherian local ring and I an ideal of R. We study how local cohomology modules with support in
$(R,\mathfrak {m})$ be a Noetherian local ring and I an ideal of R. We study how local cohomology modules with support in 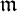 $\mathfrak {m}$ change for small perturbations J of I, that is, for ideals J such that
$\mathfrak {m}$ change for small perturbations J of I, that is, for ideals J such that 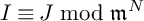 $I\equiv J\bmod \mathfrak {m}^N$ for large N, under the hypothesis that
$I\equiv J\bmod \mathfrak {m}^N$ for large N, under the hypothesis that 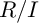 $R/I$ and
$R/I$ and 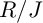 $R/J$ share the same Hilbert function. As one of our main results, we show that if
$R/J$ share the same Hilbert function. As one of our main results, we show that if 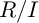 $R/I$ is generalized Cohen–Macaulay, then the local cohomology modules of
$R/I$ is generalized Cohen–Macaulay, then the local cohomology modules of 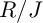 $R/J$ are isomorphic to the corresponding local cohomology modules of
$R/J$ are isomorphic to the corresponding local cohomology modules of 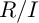 $R/I$, except possibly the top one. In particular, this answers a question raised by Quy and V. D. Trung. Our approach also allows us to prove that if
$R/I$, except possibly the top one. In particular, this answers a question raised by Quy and V. D. Trung. Our approach also allows us to prove that if 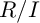 $R/I$ is Buchsbaum, then so is
$R/I$ is Buchsbaum, then so is 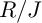 $R/J$. Finally, under some additional assumptions, we show that if
$R/J$. Finally, under some additional assumptions, we show that if 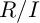 $R/I$ satisfies Serre’s property
$R/I$ satisfies Serre’s property 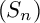 $(S_n)$, then so does
$(S_n)$, then so does 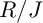 $R/J$.
$R/J$.