Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mason, J. D.
and
Yimin, Xiao
2002.
Sample Path Properties of Operator-Slef-Similar Gaussian Random Fields.
Theory of Probability & Its Applications,
Vol. 46,
Issue. 1,
p.
58.
Guillotin-Plantard, Nadine
and
Ladret, Véronique
2005.
Limit theorems for U-statistics indexed by a one dimensional random walk.
ESAIM: Probability and Statistics,
Vol. 9,
Issue. ,
p.
98.
Franke, Brice
and
Saigo, Tatsuhiko
2009.
The extremes of random walks in random sceneries.
Advances in Applied Probability,
Vol. 41,
Issue. 2,
p.
452.
Franke, Brice
and
Saigo, Tatsuhiko
2009.
The extremes of random walks in random sceneries.
Advances in Applied Probability,
Vol. 41,
Issue. 2,
p.
452.
Dombry, Clement
and
Guillotin-Plantard, Nadine
2009.
A functional approach for random walks in random sceneries.
Electronic Journal of Probability,
Vol. 14,
Issue. none,
Guillotin-Plantard, Nadine
and
Prieur, Clémentine
2010.
Limit theorem for random walk in weakly dependent random scenery.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 46,
Issue. 4,
Franke, Brice
and
Saigo, Tatsuhiko
2010.
A self-similar process arising from a random walk with random environment in random scenery.
Bernoulli,
Vol. 16,
Issue. 3,
Didier, Gustavo
and
Pipiras, Vladas
2012.
Exponents, Symmetry Groups and Classification of Operator Fractional Brownian Motions.
Journal of Theoretical Probability,
Vol. 25,
Issue. 2,
p.
353.
Lindquist, W. Brent
and
Rachev, Svetlozar T.
2021.
Taylor’s law and heavy-tailed distributions.
Proceedings of the National Academy of Sciences,
Vol. 118,
Issue. 50,


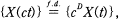
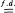 means the equality for all finite-dimensional distributions and
means the equality for all finite-dimensional distributions and