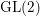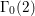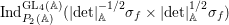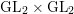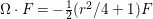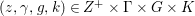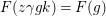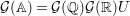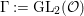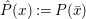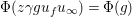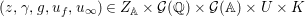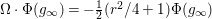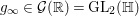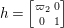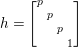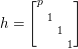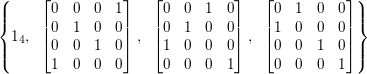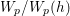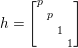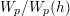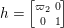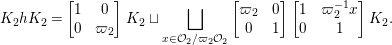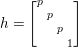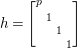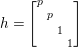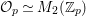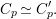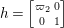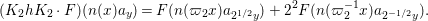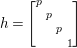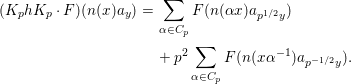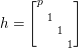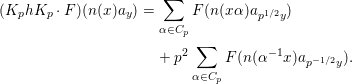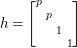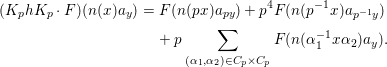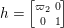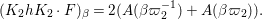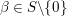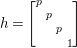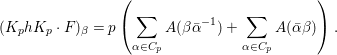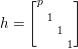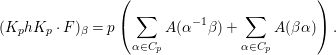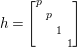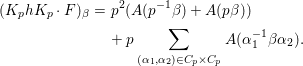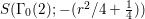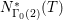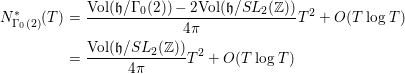1 Introduction
One of the fundamental problems in the theory of automorphic forms or representations is to study the Ramanujan conjecture. To review it, let ![]() ${\mathcal{G}}$ be a reductive algebraic group over a number field
${\mathcal{G}}$ be a reductive algebraic group over a number field ![]() $F$, and let
$F$, and let 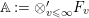 $\mathbb{A}:=\otimes _{v\leqslant \infty }^{\prime }F_{v}$ be the ring of adeles for
$\mathbb{A}:=\otimes _{v\leqslant \infty }^{\prime }F_{v}$ be the ring of adeles for ![]() $F$, where
$F$, where ![]() $F_{v}$ denotes the local field at a place
$F_{v}$ denotes the local field at a place ![]() $v$. The study of the Ramanujan conjecture is to consider the following question.
$v$. The study of the Ramanujan conjecture is to consider the following question.
Question.
Let 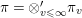 ${\it\pi}=\otimes _{v\leqslant \infty }^{\prime }{\it\pi}_{v}$ be an irreducible cuspidal representation of
${\it\pi}=\otimes _{v\leqslant \infty }^{\prime }{\it\pi}_{v}$ be an irreducible cuspidal representation of ![]() ${\mathcal{G}}(\mathbb{A})$, where
${\mathcal{G}}(\mathbb{A})$, where ![]() ${\it\pi}_{v}$ denotes the local component of
${\it\pi}_{v}$ denotes the local component of ![]() ${\it\pi}$ at a place
${\it\pi}$ at a place ![]() $v$. Then, is
$v$. Then, is ![]() ${\it\pi}_{v}$ tempered for every
${\it\pi}_{v}$ tempered for every ![]() $v\leqslant \infty$?
$v\leqslant \infty$?
Nowadays it is widely known that there are cuspidal representations or cusp forms answering negatively to this question, which we call counterexamples to the Ramanujan conjecture. A well-known example is given by the Saito–Kurokawa lifting to holomorphic Siegel cusp forms of degree two (cf. [Reference Kurokawa17]). Another well-known example is the work by Howe and Piatetski-Shapiro [Reference Howe and Piatetski-Shapiro11], which gives a counterexample by a theta lifting from ![]() $\text{O}(2)$ to
$\text{O}(2)$ to ![]() $\text{Sp}(4)$. In fact, it is expected that liftings from automorphic forms on a smaller group provide such counterexamples. On the other hand, let us recall that there is the notion of CAP representation (cuspidal representation associated to a parabolic subgroup), which was originally introduced by Piatetski-Shapiro [Reference Piatetski-Shapiro25]. This is a representation theoretic approach to find counterexamples to the Ramanujan conjecture.
$\text{Sp}(4)$. In fact, it is expected that liftings from automorphic forms on a smaller group provide such counterexamples. On the other hand, let us recall that there is the notion of CAP representation (cuspidal representation associated to a parabolic subgroup), which was originally introduced by Piatetski-Shapiro [Reference Piatetski-Shapiro25]. This is a representation theoretic approach to find counterexamples to the Ramanujan conjecture.
We now note that the Ramanujan conjecture for the general linear group ![]() $\text{GL}(n)$ is strongly believed. In fact, by Jacquet and Shalika [Reference Jacquet and Shalika14], it can be shown that the CAP phenomenon never occurs for
$\text{GL}(n)$ is strongly believed. In fact, by Jacquet and Shalika [Reference Jacquet and Shalika14], it can be shown that the CAP phenomenon never occurs for ![]() $\text{GL}(n)$. More generally, it is expected that the conjecture would hold for generic cuspidal representations of quasisplit reductive groups, which should be referred to as the generalized Ramanujan conjecture. In view of the Langlands functoriality principle for quasisplit groups and their inner forms, the Ramanujan conjecture for the inner forms is quite natural and interesting to study, as well as CAP representations. To define the notion of CAP representations for the inner forms we follow Gan [Reference Gan8] and Pitale [Reference Pitale22] (cf. Definition 6.6). Let us note that the Saito–Kurokawa lifting deals with the case of the split symplectic group
$\text{GL}(n)$. More generally, it is expected that the conjecture would hold for generic cuspidal representations of quasisplit reductive groups, which should be referred to as the generalized Ramanujan conjecture. In view of the Langlands functoriality principle for quasisplit groups and their inner forms, the Ramanujan conjecture for the inner forms is quite natural and interesting to study, as well as CAP representations. To define the notion of CAP representations for the inner forms we follow Gan [Reference Gan8] and Pitale [Reference Pitale22] (cf. Definition 6.6). Let us note that the Saito–Kurokawa lifting deals with the case of the split symplectic group ![]() $\text{GSp}(4)$ of degree two. The case of the nonsplit inner form
$\text{GSp}(4)$ of degree two. The case of the nonsplit inner form 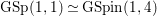 $\text{GSp}(1,1)\simeq \text{GSpin}(1,4)$ of
$\text{GSp}(1,1)\simeq \text{GSpin}(1,4)$ of ![]() $\text{GSp}(4)$ is considered in [Reference Gan8] and [Reference Pitale22].
$\text{GSp}(4)$ is considered in [Reference Gan8] and [Reference Pitale22].
In this paper we take up the case of 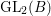 $\text{GL}_{2}(B)$ over the division quaternion algebra
$\text{GL}_{2}(B)$ over the division quaternion algebra ![]() $B$ with discriminant two. Note that
$B$ with discriminant two. Note that 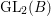 $\text{GL}_{2}(B)$ is an inner form of the split group
$\text{GL}_{2}(B)$ is an inner form of the split group ![]() $\text{GL}(4)$. Our results provide an explicit construction of cusp forms on
$\text{GL}(4)$. Our results provide an explicit construction of cusp forms on 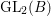 $\text{GL}_{2}(B)$ lifted from Maass cusp forms for the congruence subgroup
$\text{GL}_{2}(B)$ lifted from Maass cusp forms for the congruence subgroup ![]() ${\rm\Gamma}_{0}(2)$, and show that the cuspidal automorphic representations generated by such lifts are CAP representations of
${\rm\Gamma}_{0}(2)$, and show that the cuspidal automorphic representations generated by such lifts are CAP representations of 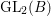 $\text{GL}_{2}(B)$. The method of our construction of the lifting follows [Reference Pitale22], which deals with an explicit construction of lifting to
$\text{GL}_{2}(B)$. The method of our construction of the lifting follows [Reference Pitale22], which deals with an explicit construction of lifting to 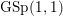 $\text{GSp}(1,1)$. In fact, note that the cusp forms constructed by our lifting are viewed as Maass cusp forms on the 5-dimensional real hyperbolic space, while the lifting considered in [Reference Pitale22] provides Maass cusp forms on the 4-dimensional real hyperbolic space. As in [Reference Pitale22], to prove the automorphy of our lifts, we use the converse theorem [Reference Maass19] by Maass, which is useful for real hyperbolic spaces of arbitrary dimension.
$\text{GSp}(1,1)$. In fact, note that the cusp forms constructed by our lifting are viewed as Maass cusp forms on the 5-dimensional real hyperbolic space, while the lifting considered in [Reference Pitale22] provides Maass cusp forms on the 4-dimensional real hyperbolic space. As in [Reference Pitale22], to prove the automorphy of our lifts, we use the converse theorem [Reference Maass19] by Maass, which is useful for real hyperbolic spaces of arbitrary dimension.
We explain the explicit construction of our lifting. Let ![]() $f$ be a Maass cusp form for
$f$ be a Maass cusp form for ![]() ${\rm\Gamma}_{0}(2)$ which is an eigenfunction of the Atkin–Lehner involution. Let
${\rm\Gamma}_{0}(2)$ which is an eigenfunction of the Atkin–Lehner involution. Let 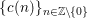 $\{c(n)\}_{n\in \mathbb{Z}\setminus \{0\}}$ be Fourier coefficients of
$\{c(n)\}_{n\in \mathbb{Z}\setminus \{0\}}$ be Fourier coefficients of ![]() $f$. From the
$f$. From the ![]() $c(n)$s we define numbers
$c(n)$s we define numbers ![]() $A({\it\beta})$ (cf. (4.2)) for
$A({\it\beta})$ (cf. (4.2)) for 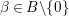 ${\it\beta}\in B\setminus \{0\}$ in order to construct our lifting to a cusp form
${\it\beta}\in B\setminus \{0\}$ in order to construct our lifting to a cusp form ![]() $F_{f}$ on
$F_{f}$ on 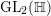 $\text{GL}_{2}(\mathbb{H})$ in the nonadelic setting. Actually, the
$\text{GL}_{2}(\mathbb{H})$ in the nonadelic setting. Actually, the ![]() $A({\it\beta})$s are nothing but Fourier coefficients of
$A({\it\beta})$s are nothing but Fourier coefficients of ![]() $F_{f}$. The statement of our first result is as follows (cf. Theorem 4.4).
$F_{f}$. The statement of our first result is as follows (cf. Theorem 4.4).
Theorem 1.1. Let ![]() $f$ be a nonzero Mass cusp form which is an eigenfunction of the Atkin–Lehner involution. Then
$f$ be a nonzero Mass cusp form which is an eigenfunction of the Atkin–Lehner involution. Then ![]() $F_{f}$ is a nonzero cusp form on
$F_{f}$ is a nonzero cusp form on 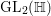 $\text{GL}_{2}(\mathbb{H})$.
$\text{GL}_{2}(\mathbb{H})$.
Another result is that the cuspidal representations generated by the ![]() $F_{f}$s are CAP representations of
$F_{f}$s are CAP representations of 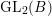 $\text{GL}_{2}(B)$ and provide counterexamples to the Ramanujan conjecture. To be more precise, assume that
$\text{GL}_{2}(B)$ and provide counterexamples to the Ramanujan conjecture. To be more precise, assume that ![]() $f$ is a Hecke eigenform. We can regard
$f$ is a Hecke eigenform. We can regard ![]() $F_{f}$ as a cusp form on the adele group
$F_{f}$ as a cusp form on the adele group ![]() ${\mathcal{G}}(\mathbb{A})$ with
${\mathcal{G}}(\mathbb{A})$ with 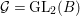 ${\mathcal{G}}=\text{GL}_{2}(B)$. We can show that
${\mathcal{G}}=\text{GL}_{2}(B)$. We can show that ![]() $F_{f}$ is a Hecke eigenform (cf. Section 5). Then, the strong multiplicity-one theorem proved by Badulescu and Renard [Reference Badulescu2], [Reference Badulescu and Renard3] implies that
$F_{f}$ is a Hecke eigenform (cf. Section 5). Then, the strong multiplicity-one theorem proved by Badulescu and Renard [Reference Badulescu2], [Reference Badulescu and Renard3] implies that ![]() $F_{f}$ generates an irreducible cuspidal representation
$F_{f}$ generates an irreducible cuspidal representation 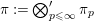 ${\it\pi}:=\otimes _{p\leqslant \infty }^{\prime }{\it\pi}_{p}$ of
${\it\pi}:=\otimes _{p\leqslant \infty }^{\prime }{\it\pi}_{p}$ of ![]() ${\mathcal{G}}(\mathbb{A})$. By our detailed study on Hecke eigenvalues of
${\mathcal{G}}(\mathbb{A})$. By our detailed study on Hecke eigenvalues of ![]() $F_{f}$, we can determine local representations
$F_{f}$, we can determine local representations ![]() ${\it\pi}_{p}$ for every
${\it\pi}_{p}$ for every ![]() $p<\infty$. We can also determine
$p<\infty$. We can also determine ![]() ${\it\pi}_{p}$ explicitly at
${\it\pi}_{p}$ explicitly at ![]() $p=\infty$ by the calculation of the eigenvalue for the Casimir operator. For this we note that every
$p=\infty$ by the calculation of the eigenvalue for the Casimir operator. For this we note that every ![]() ${\it\pi}_{p}$ is unramified (at
${\it\pi}_{p}$ is unramified (at ![]() $p<\infty$) or spherical (at
$p<\infty$) or spherical (at ![]() $p=\infty$). We can show that
$p=\infty$). We can show that ![]() ${\it\pi}_{p}$ (respectively
${\it\pi}_{p}$ (respectively ![]() ${\it\pi}_{\infty }$) is nontempered at every odd prime
${\it\pi}_{\infty }$) is nontempered at every odd prime ![]() $p$ (respectively tempered at
$p$ (respectively tempered at ![]() $p=\infty$). If we further assume that
$p=\infty$). If we further assume that ![]() $f$ is a new form, we can also show the nontemperedness of
$f$ is a new form, we can also show the nontemperedness of ![]() ${\it\pi}_{p}$ at
${\it\pi}_{p}$ at ![]() $p=2$. These lead to the following theorem (cf. Theorems 6.7, 6.8).
$p=2$. These lead to the following theorem (cf. Theorems 6.7, 6.8).
(1) Let
 $f$ be a nonzero Hecke eigen cusp form, and let
$f$ be a nonzero Hecke eigen cusp form, and let  $F_{f}$ be the lift. Let
$F_{f}$ be the lift. Let  ${\it\sigma}_{f}$ and
${\it\sigma}_{f}$ and  ${\it\pi}_{F}$ be irreducible cuspidal representations generated by
${\it\pi}_{F}$ be irreducible cuspidal representations generated by  $f$ and
$f$ and  $F=F_{f}$ respectively. Then
$F=F_{f}$ respectively. Then  ${\it\pi}_{F}$ is nearly equivalent to an irreducible constituent of
${\it\pi}_{F}$ is nearly equivalent to an irreducible constituent of  $\text{Ind}_{P_{2}(\mathbb{A})}^{\text{GL}_{4}(\mathbb{A})}(|\text{det}|_{\mathbb{A}}^{-1/2}{\it\sigma}_{f}\times |\text{det}|_{\mathbb{A}}^{1/2}{\it\sigma}_{f})$. Here,
$\text{Ind}_{P_{2}(\mathbb{A})}^{\text{GL}_{4}(\mathbb{A})}(|\text{det}|_{\mathbb{A}}^{-1/2}{\it\sigma}_{f}\times |\text{det}|_{\mathbb{A}}^{1/2}{\it\sigma}_{f})$. Here,  $P_{2}$ is the standard parabolic subgroup of
$P_{2}$ is the standard parabolic subgroup of  $\text{GL}_{4}$ with Levi subgroup
$\text{GL}_{4}$ with Levi subgroup  $\text{GL}_{2}\times \text{GL}_{2}$. Namely
$\text{GL}_{2}\times \text{GL}_{2}$. Namely  ${\it\pi}_{F}$ is a CAP representation.
${\it\pi}_{F}$ is a CAP representation.(2) The cuspidal representations
 ${\it\pi}_{F}$ are counterexamples to the Ramanujan conjecture.
${\it\pi}_{F}$ are counterexamples to the Ramanujan conjecture.
Let ![]() ${\it\pi}^{\prime }$ be the unique irreducible quotient of
${\it\pi}^{\prime }$ be the unique irreducible quotient of 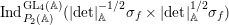 $\text{Ind}_{P_{2}(\mathbb{A})}^{\text{GL}_{4}(\mathbb{A})}(|\text{det}|_{\mathbb{A}}^{-1/2}{\it\sigma}_{f}\times |\text{det}|_{\mathbb{A}}^{1/2}{\it\sigma}_{f})$. This is denoted by
$\text{Ind}_{P_{2}(\mathbb{A})}^{\text{GL}_{4}(\mathbb{A})}(|\text{det}|_{\mathbb{A}}^{-1/2}{\it\sigma}_{f}\times |\text{det}|_{\mathbb{A}}^{1/2}{\it\sigma}_{f})$. This is denoted by 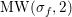 $\text{MW}({\it\sigma}_{f},2)$ in [Reference Badulescu and Renard3, §18]. Then
$\text{MW}({\it\sigma}_{f},2)$ in [Reference Badulescu and Renard3, §18]. Then ![]() ${\it\pi}^{\prime }$ is a noncuspidal, discrete series representation of
${\it\pi}^{\prime }$ is a noncuspidal, discrete series representation of  $\text{GL}_{4}(\mathbb{A})$. Since
$\text{GL}_{4}(\mathbb{A})$. Since ![]() ${\it\sigma}_{f}$ is not the image of a cuspidal representation of
${\it\sigma}_{f}$ is not the image of a cuspidal representation of ![]() $B_{\mathbb{A}}^{\times }$ under the Jacquet–Langlands correspondence,
$B_{\mathbb{A}}^{\times }$ under the Jacquet–Langlands correspondence, ![]() ${\it\pi}^{\prime }$ is
${\it\pi}^{\prime }$ is ![]() $B$-compatible according to [Reference Badulescu and Renard3, Proposition 18.2, part (a)]. Hence, there exists a discrete series representation
$B$-compatible according to [Reference Badulescu and Renard3, Proposition 18.2, part (a)]. Hence, there exists a discrete series representation ![]() ${\it\pi}$ of
${\it\pi}$ of 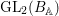 $\text{GL}_{2}(B_{\mathbb{A}})$ which maps to
$\text{GL}_{2}(B_{\mathbb{A}})$ which maps to ![]() ${\it\pi}^{\prime }$ under the Jacquet–Langlands correspondence. Moreover, from [Reference Badulescu and Renard3, Proposition 18.2, part (b)], the representation
${\it\pi}^{\prime }$ under the Jacquet–Langlands correspondence. Moreover, from [Reference Badulescu and Renard3, Proposition 18.2, part (b)], the representation ![]() ${\it\pi}$ has to be cuspidal. By the strong multiplicity-one theorem for
${\it\pi}$ has to be cuspidal. By the strong multiplicity-one theorem for 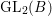 $\text{GL}_{2}(B)$, the representation
$\text{GL}_{2}(B)$, the representation ![]() ${\it\pi}$ has to be exactly the same as
${\it\pi}$ has to be exactly the same as ![]() ${\it\pi}_{F}$ obtained from the classical construction. The novelty of our method is that we obtain an explicit formula for the lift in terms of Fourier expansions which are valid for non-Hecke eigenforms as well. In addition, the classical method immediately shows that the lifting is a linear nonzero map.
${\it\pi}_{F}$ obtained from the classical construction. The novelty of our method is that we obtain an explicit formula for the lift in terms of Fourier expansions which are valid for non-Hecke eigenforms as well. In addition, the classical method immediately shows that the lifting is a linear nonzero map.
Let us remark that Grobner [Reference Grobner9] has also obtained examples of CAP representations for 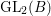 $\text{GL}_{2}(B)$ using the results of [Reference Badulescu and Renard3]. The example by Grobner [Reference Grobner9] has a nontempered local component at the archimedean place, while our cuspidal representation
$\text{GL}_{2}(B)$ using the results of [Reference Badulescu and Renard3]. The example by Grobner [Reference Grobner9] has a nontempered local component at the archimedean place, while our cuspidal representation ![]() ${\it\pi}$ has a tempered local component at the archimedean place, as is remarked above.
${\it\pi}$ has a tempered local component at the archimedean place, as is remarked above.
In terms of representation theory, one naturally asks whether our classical construction of the lifting is understood by a theta lifting. It is shown in [Reference Piatetski-Shapiro25] that the classical Saito–Kurokawa lifting is a theta lifting. In addition, [Reference Gan8] shows that the classical lifting to 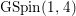 $\text{GSpin}(1,4)$ obtained in [Reference Pitale22] is also a theta lifting. We expect that the lifting constructed in this paper is also a theta lifting given by the theta correspondence between
$\text{GSpin}(1,4)$ obtained in [Reference Pitale22] is also a theta lifting. We expect that the lifting constructed in this paper is also a theta lifting given by the theta correspondence between ![]() $SL(2)$ and the orthogonal group
$SL(2)$ and the orthogonal group ![]() $O(5,1)$ with the Witt index
$O(5,1)$ with the Witt index ![]() $(5,1)$. One might have to use the techniques from [Reference Gan8] to prove such a result. We do not address this question in the current paper.
$(5,1)$. One might have to use the techniques from [Reference Gan8] to prove such a result. We do not address this question in the current paper.
The outline of this paper is as follows. In Section 2, we first introduce the basic notation of algebraic groups and Lie groups. Next, we introduce the automorphic forms that concern us in this paper. In Section 3, we study a zeta integral attached to a Maass cusp form. This is needed in order to apply Maass converse theorem. Then, the explicit construction of cusp forms on 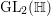 $\text{GL}_{2}(\mathbb{H})$ is given by lifts
$\text{GL}_{2}(\mathbb{H})$ is given by lifts ![]() $F_{f}$ in Section 4. In Section 5, we view
$F_{f}$ in Section 4. In Section 5, we view ![]() $F_{f}$ as a cusp form on the adele group
$F_{f}$ as a cusp form on the adele group ![]() ${\mathcal{G}}(\mathbb{A})$ and prove that, given a Hecke eigenform
${\mathcal{G}}(\mathbb{A})$ and prove that, given a Hecke eigenform ![]() $f$,
$f$, ![]() $F_{f}$ is also a Hecke eigenform at every finite place. Then, in Section 6, we determine the local components
$F_{f}$ is also a Hecke eigenform at every finite place. Then, in Section 6, we determine the local components ![]() ${\it\pi}_{p}$ of the cuspidal representation
${\it\pi}_{p}$ of the cuspidal representation ![]() ${\it\pi}$ generated by
${\it\pi}$ generated by ![]() $F_{f}$ for all places
$F_{f}$ for all places ![]() $p\leqslant \infty$. We thus see that
$p\leqslant \infty$. We thus see that ![]() ${\it\pi}$ is a CAP representation and provides a counterexample to the Ramanujan conjecture.
${\it\pi}$ is a CAP representation and provides a counterexample to the Ramanujan conjecture.
2 Basic notations
2.1 Algebraic groups, real Lie groups and the 5-dimensional hyperbolic space
Let ![]() $B$ be the definite quaternion algebra over
$B$ be the definite quaternion algebra over ![]() $\mathbb{Q}$ with discriminant
$\mathbb{Q}$ with discriminant ![]() $d_{B}=2$. The algebra
$d_{B}=2$. The algebra ![]() $B$ is given by
$B$ is given by 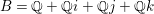 $B=\mathbb{Q}+\mathbb{Q}i+\mathbb{Q}j+\mathbb{Q}k$ with a basis
$B=\mathbb{Q}+\mathbb{Q}i+\mathbb{Q}j+\mathbb{Q}k$ with a basis 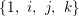 $\{1,~i,~j,~k\}$ characterized by the conditions
$\{1,~i,~j,~k\}$ characterized by the conditions
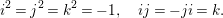 $$\begin{eqnarray}i^{2}=j^{2}=k^{2}=-1,\quad ij=-ji=k.\end{eqnarray}$$
$$\begin{eqnarray}i^{2}=j^{2}=k^{2}=-1,\quad ij=-ji=k.\end{eqnarray}$$ Let ![]() ${\mathcal{G}}$ be the
${\mathcal{G}}$ be the ![]() $\mathbb{Q}$-algebraic group defined by its group of
$\mathbb{Q}$-algebraic group defined by its group of ![]() $\mathbb{Q}$-rational points
$\mathbb{Q}$-rational points
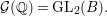 $$\begin{eqnarray}{\mathcal{G}}(\mathbb{Q})=\text{GL}_{2}(B).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{G}}(\mathbb{Q})=\text{GL}_{2}(B).\end{eqnarray}$$ Here, 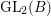 $\text{GL}_{2}(B)$ is the general linear group over
$\text{GL}_{2}(B)$ is the general linear group over ![]() $B$, which consists of elements in
$B$, which consists of elements in ![]() $M_{2}(B)$ whose reduced norms are nonzero. Let
$M_{2}(B)$ whose reduced norms are nonzero. Let 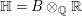 $\mathbb{H}=B\otimes _{\mathbb{Q}}\mathbb{R}$, which is nothing but the Hamilton quaternion algebra
$\mathbb{H}=B\otimes _{\mathbb{Q}}\mathbb{R}$, which is nothing but the Hamilton quaternion algebra 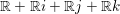 $\mathbb{R}+\mathbb{R}i+\mathbb{R}j+\mathbb{R}k$. Let
$\mathbb{R}+\mathbb{R}i+\mathbb{R}j+\mathbb{R}k$. Let 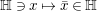 $\mathbb{H}\ni x\mapsto \bar{x}\in \mathbb{H}$ denote the main involution of
$\mathbb{H}\ni x\mapsto \bar{x}\in \mathbb{H}$ denote the main involution of ![]() $\mathbb{H}$, and let
$\mathbb{H}$, and let 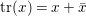 $\operatorname{tr}(x)=x+\bar{x}$ and
$\operatorname{tr}(x)=x+\bar{x}$ and 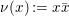 ${\it\nu}(x):=x\bar{x}$ be the reduced trace and the reduced norm of
${\it\nu}(x):=x\bar{x}$ be the reduced trace and the reduced norm of ![]() $x\in \mathbb{H}$ respectively. In what follows, we often use the notation
$x\in \mathbb{H}$ respectively. In what follows, we often use the notation 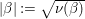 $|{\it\beta}|:=\sqrt{{\it\nu}({\it\beta})}$ for
$|{\it\beta}|:=\sqrt{{\it\nu}({\it\beta})}$ for ![]() ${\it\beta}\in \mathbb{H}$. We put
${\it\beta}\in \mathbb{H}$. We put  $\mathbb{H}^{-}:=\{x\in \mathbb{H}\mid \operatorname{tr}(x)=0\}$ to be the set of pure quaternions, and
$\mathbb{H}^{-}:=\{x\in \mathbb{H}\mid \operatorname{tr}(x)=0\}$ to be the set of pure quaternions, and  $\mathbb{H}^{1}:=\{x\in \mathbb{H}\mid {\it\nu}(x)=1\}$.
$\mathbb{H}^{1}:=\{x\in \mathbb{H}\mid {\it\nu}(x)=1\}$.
Denote by 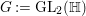 $G:=\text{GL}_{2}(\mathbb{H})$ the general linear group of degree two with coefficients in the Hamilton quaternion algebra
$G:=\text{GL}_{2}(\mathbb{H})$ the general linear group of degree two with coefficients in the Hamilton quaternion algebra ![]() $\mathbb{H}$. The Lie group
$\mathbb{H}$. The Lie group ![]() $G$ admits an Iwasawa decomposition
$G$ admits an Iwasawa decomposition
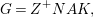 $$\begin{eqnarray}G=Z^{+}NAK,\end{eqnarray}$$
$$\begin{eqnarray}G=Z^{+}NAK,\end{eqnarray}$$where
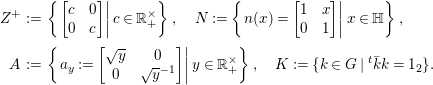 $$\begin{eqnarray}\displaystyle \quad Z^{+} & := & \displaystyle \displaystyle \left\{\left.\left[\begin{array}{@{}cc@{}}c & 0\\ 0 & c\end{array}\right]\right|c\in \mathbb{R}_{+}^{\times }\right\},\quad N:=\left\{\left.n(x)=\left[\begin{array}{@{}cc@{}}1 & x\\ 0 & 1\end{array}\right]\right|x\in \mathbb{H}\right\},\nonumber\\ \displaystyle A & := & \displaystyle \displaystyle \left\{\left.a_{y}:=\left[\begin{array}{@{}cc@{}}\sqrt{y} & 0\\ 0 & \sqrt{y}^{-1}\end{array}\right]\right|y\in \mathbb{R}_{+}^{\times }\right\},\quad K:=\{k\in G\mid \text{}^{t}\bar{k}k=1_{2}\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \quad Z^{+} & := & \displaystyle \displaystyle \left\{\left.\left[\begin{array}{@{}cc@{}}c & 0\\ 0 & c\end{array}\right]\right|c\in \mathbb{R}_{+}^{\times }\right\},\quad N:=\left\{\left.n(x)=\left[\begin{array}{@{}cc@{}}1 & x\\ 0 & 1\end{array}\right]\right|x\in \mathbb{H}\right\},\nonumber\\ \displaystyle A & := & \displaystyle \displaystyle \left\{\left.a_{y}:=\left[\begin{array}{@{}cc@{}}\sqrt{y} & 0\\ 0 & \sqrt{y}^{-1}\end{array}\right]\right|y\in \mathbb{R}_{+}^{\times }\right\},\quad K:=\{k\in G\mid \text{}^{t}\bar{k}k=1_{2}\}.\end{eqnarray}$$ The subgroup ![]() $Z^{+}$ is contained in the center of
$Z^{+}$ is contained in the center of ![]() $G$, and
$G$, and ![]() $K$ is a maximal compact subgroup of
$K$ is a maximal compact subgroup of ![]() $G$, which is isomorphic to the definite symplectic group of degree two.
$G$, which is isomorphic to the definite symplectic group of degree two.
Let us consider the quotient 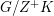 $G/Z^{+}K$, which is realized as
$G/Z^{+}K$, which is realized as
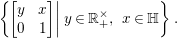 $$\begin{eqnarray}\left\{\left.\!\left[\begin{array}{@{}cc@{}}y & x\\ 0 & 1\end{array}\right]\right|y\in \mathbb{R}_{+}^{\times },~x\in \mathbb{H}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\left.\!\left[\begin{array}{@{}cc@{}}y & x\\ 0 & 1\end{array}\right]\right|y\in \mathbb{R}_{+}^{\times },~x\in \mathbb{H}\right\}.\end{eqnarray}$$This gives a realization of the 5-dimensional real hyperbolic space.
2.2 Lie algebras
The Lie algebra ![]() $\mathfrak{g}$ of
$\mathfrak{g}$ of ![]() $G$ is nothing but
$G$ is nothing but ![]() $M_{2}(\mathbb{H})$, and has an Iwasawa decomposition
$M_{2}(\mathbb{H})$, and has an Iwasawa decomposition
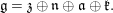 $$\begin{eqnarray}\mathfrak{g}=\mathfrak{z}\oplus \mathfrak{n}\oplus \mathfrak{a}\oplus \mathfrak{k}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}=\mathfrak{z}\oplus \mathfrak{n}\oplus \mathfrak{a}\oplus \mathfrak{k}.\end{eqnarray}$$Here,
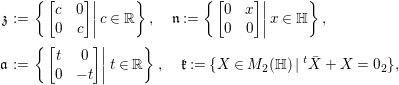 $$\begin{eqnarray}\displaystyle \mathfrak{z} & := & \displaystyle \left\{\left.\left[\begin{array}{@{}cc@{}}c & 0\\ 0 & c\end{array}\right]\right|c\in \mathbb{R}\right\},\quad \mathfrak{n}:=\left\{\left.\left[\begin{array}{@{}cc@{}}0 & x\\ 0 & 0\end{array}\right]\right|x\in \mathbb{H}\right\},\nonumber\\ \displaystyle \mathfrak{a} & := & \displaystyle \left\{\left.\left[\begin{array}{@{}cc@{}}t & 0\\ 0 & -t\end{array}\right]\right|t\in \mathbb{R}\right\},\quad \mathfrak{k}:=\{X\in M_{2}(\mathbb{H})\mid \text{}^{t}\bar{X}+X=0_{2}\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{z} & := & \displaystyle \left\{\left.\left[\begin{array}{@{}cc@{}}c & 0\\ 0 & c\end{array}\right]\right|c\in \mathbb{R}\right\},\quad \mathfrak{n}:=\left\{\left.\left[\begin{array}{@{}cc@{}}0 & x\\ 0 & 0\end{array}\right]\right|x\in \mathbb{H}\right\},\nonumber\\ \displaystyle \mathfrak{a} & := & \displaystyle \left\{\left.\left[\begin{array}{@{}cc@{}}t & 0\\ 0 & -t\end{array}\right]\right|t\in \mathbb{R}\right\},\quad \mathfrak{k}:=\{X\in M_{2}(\mathbb{H})\mid \text{}^{t}\bar{X}+X=0_{2}\},\end{eqnarray}$$ where ![]() $\mathfrak{z},~\mathfrak{n},~\mathfrak{a}$ and
$\mathfrak{z},~\mathfrak{n},~\mathfrak{a}$ and ![]() $\mathfrak{k}$ are the Lie algebras of
$\mathfrak{k}$ are the Lie algebras of  $Z^{+},~N,~A$ and
$Z^{+},~N,~A$ and ![]() $K$ respectively.
$K$ respectively.
We next consider the root space decomposition of ![]() $\mathfrak{g}$ with respect to
$\mathfrak{g}$ with respect to ![]() $\mathfrak{a}$. Let
$\mathfrak{a}$. Let 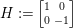 $H:=\left[\!\begin{smallmatrix}1 & 0\phantom{}\\ 0 & -1\end{smallmatrix}\!\right]$, and let
$H:=\left[\!\begin{smallmatrix}1 & 0\phantom{}\\ 0 & -1\end{smallmatrix}\!\right]$, and let ![]() ${\it\alpha}$ be the linear form of
${\it\alpha}$ be the linear form of ![]() $\mathfrak{a}$ such that
$\mathfrak{a}$ such that 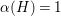 ${\it\alpha}(H)=1$. Then
${\it\alpha}(H)=1$. Then ![]() $\{\pm 2{\it\alpha}\}$ is the set of roots for
$\{\pm 2{\it\alpha}\}$ is the set of roots for ![]() $(\mathfrak{g},\mathfrak{a})$. For
$(\mathfrak{g},\mathfrak{a})$. For ![]() $z\in \mathbb{H}$ we put
$z\in \mathbb{H}$ we put
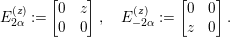 $$\begin{eqnarray}E_{2{\it\alpha}}^{(z)}:=\left[\begin{array}{@{}cc@{}}0 & z\\ 0 & 0\end{array}\right],\quad E_{-2{\it\alpha}}^{(z)}:=\left[\begin{array}{@{}cc@{}}0 & 0\\ z & 0\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}E_{2{\it\alpha}}^{(z)}:=\left[\begin{array}{@{}cc@{}}0 & z\\ 0 & 0\end{array}\right],\quad E_{-2{\it\alpha}}^{(z)}:=\left[\begin{array}{@{}cc@{}}0 & 0\\ z & 0\end{array}\right].\end{eqnarray}$$ The set 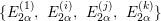 $\{E_{2{\it\alpha}}^{(1)},~E_{2{\it\alpha}}^{(i)},~E_{2{\it\alpha}}^{(j)},~E_{2{\it\alpha}}^{(k)}\}$ (respectively
$\{E_{2{\it\alpha}}^{(1)},~E_{2{\it\alpha}}^{(i)},~E_{2{\it\alpha}}^{(j)},~E_{2{\it\alpha}}^{(k)}\}$ (respectively 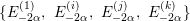 $\{E_{-2{\it\alpha}}^{(1)},~E_{-2{\it\alpha}}^{(i)},~E_{-2{\it\alpha}}^{(j)},~E_{-2{\it\alpha}}^{(k)}\}$) forms a basis of
$\{E_{-2{\it\alpha}}^{(1)},~E_{-2{\it\alpha}}^{(i)},~E_{-2{\it\alpha}}^{(j)},~E_{-2{\it\alpha}}^{(k)}\}$) forms a basis of ![]() $\mathfrak{n}$ (respectively a basis of
$\mathfrak{n}$ (respectively a basis of 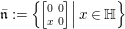 $\bar{\mathfrak{n}}:=\left\{\left.\!\left[\!\begin{smallmatrix}0 & 0\phantom{}\\ x & 0\end{smallmatrix}\!\right]\right|x\in \mathbb{H}\right\}\!$). Let
$\bar{\mathfrak{n}}:=\left\{\left.\!\left[\!\begin{smallmatrix}0 & 0\phantom{}\\ x & 0\end{smallmatrix}\!\right]\right|x\in \mathbb{H}\right\}\!$). Let 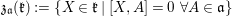 $\mathfrak{z}_{\mathfrak{a}}(\mathfrak{k}):=\{X\in \mathfrak{k}\mid [X,A]=0~\forall A\in \mathfrak{a}\}$, which coincides with
$\mathfrak{z}_{\mathfrak{a}}(\mathfrak{k}):=\{X\in \mathfrak{k}\mid [X,A]=0~\forall A\in \mathfrak{a}\}$, which coincides with
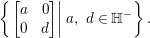 $$\begin{eqnarray}\left\{\left.\left[\begin{array}{@{}cc@{}}a & 0\\ 0 & d\end{array}\right]\right|a,~d\in \mathbb{H}^{-}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\left.\left[\begin{array}{@{}cc@{}}a & 0\\ 0 & d\end{array}\right]\right|a,~d\in \mathbb{H}^{-}\right\}.\end{eqnarray}$$ Then 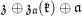 $\mathfrak{z}\oplus \mathfrak{z}_{\mathfrak{a}}(\mathfrak{k})\oplus \mathfrak{a}$ is the eigen space with the eigenvalue zero. We then see from the root space decomposition of
$\mathfrak{z}\oplus \mathfrak{z}_{\mathfrak{a}}(\mathfrak{k})\oplus \mathfrak{a}$ is the eigen space with the eigenvalue zero. We then see from the root space decomposition of ![]() $\mathfrak{g}$ with respect to
$\mathfrak{g}$ with respect to ![]() $\mathfrak{a}$ that
$\mathfrak{a}$ that ![]() $\mathfrak{g}$ decomposes into
$\mathfrak{g}$ decomposes into
 $$\begin{eqnarray}\mathfrak{g}=(\mathfrak{z}\oplus \mathfrak{z}_{\mathfrak{a}}(\mathfrak{k})\oplus \mathfrak{a})\oplus \mathfrak{n}\oplus \bar{\mathfrak{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}=(\mathfrak{z}\oplus \mathfrak{z}_{\mathfrak{a}}(\mathfrak{k})\oplus \mathfrak{a})\oplus \mathfrak{n}\oplus \bar{\mathfrak{n}}.\end{eqnarray}$$ We also introduce the simple Lie group ![]() $\text{SL}_{2}(\mathbb{H})$ consisting of elements in
$\text{SL}_{2}(\mathbb{H})$ consisting of elements in 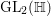 $\text{GL}_{2}(\mathbb{H})$ with their reduced norms
$\text{GL}_{2}(\mathbb{H})$ with their reduced norms ![]() $1$. The Lie algebra
$1$. The Lie algebra 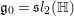 $\mathfrak{g}_{0}=\mathfrak{s}l_{2}(\mathbb{H})$ of
$\mathfrak{g}_{0}=\mathfrak{s}l_{2}(\mathbb{H})$ of ![]() $\text{SL}_{2}(\mathbb{H})$ is the Lie algebra consisting of elements in
$\text{SL}_{2}(\mathbb{H})$ is the Lie algebra consisting of elements in ![]() $M_{2}(\mathbb{H})$ with their reduced traces zero. For this we note that
$M_{2}(\mathbb{H})$ with their reduced traces zero. For this we note that
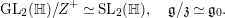 $$\begin{eqnarray}\text{GL}_{2}(\mathbb{H})/Z^{+}\simeq \text{SL}_{2}(\mathbb{H}),\quad \mathfrak{g}/\mathfrak{z}\simeq \mathfrak{g}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\text{GL}_{2}(\mathbb{H})/Z^{+}\simeq \text{SL}_{2}(\mathbb{H}),\quad \mathfrak{g}/\mathfrak{z}\simeq \mathfrak{g}_{0}.\end{eqnarray}$$ We introduce the differential operator ![]() ${\rm\Omega}$ defined by the infinitesimal action of
${\rm\Omega}$ defined by the infinitesimal action of
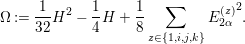 $$\begin{eqnarray}{\rm\Omega}:=\frac{1}{32}H^{2}-\frac{1}{4}H+\frac{1}{8}\mathop{\sum }_{z\in \{1,i,j,k\}}{E_{2{\it\alpha}}^{(z)}}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Omega}:=\frac{1}{32}H^{2}-\frac{1}{4}H+\frac{1}{8}\mathop{\sum }_{z\in \{1,i,j,k\}}{E_{2{\it\alpha}}^{(z)}}^{2}.\end{eqnarray}$$ This differential operator ![]() ${\rm\Omega}$ coincides with the infinitesimal action of the Casimir element of
${\rm\Omega}$ coincides with the infinitesimal action of the Casimir element of ![]() $\mathfrak{g}_{0}$ (see [Reference Knapp15, p. 293, Proposition 5.28]) on the space of right
$\mathfrak{g}_{0}$ (see [Reference Knapp15, p. 293, Proposition 5.28]) on the space of right ![]() $K$-invariant smooth functions of
$K$-invariant smooth functions of ![]() $G/Z^{+}$. To check this we note that
$G/Z^{+}$. To check this we note that 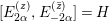 $[E_{2{\it\alpha}}^{(z)},E_{-2{\it\alpha}}^{(\bar{z})}]=H$ for
$[E_{2{\it\alpha}}^{(z)},E_{-2{\it\alpha}}^{(\bar{z})}]=H$ for ![]() $z\in \mathbb{H}^{1}$ and Iwasawa decompositions
$z\in \mathbb{H}^{1}$ and Iwasawa decompositions 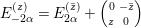 $E_{-2{\it\alpha}}^{(z)}=E_{2{\it\alpha}}^{(\bar{z})}+\left(\!\begin{smallmatrix}0 & -\bar{z}\phantom{}\\ z & 0\end{smallmatrix}\!\right)$ for
$E_{-2{\it\alpha}}^{(z)}=E_{2{\it\alpha}}^{(\bar{z})}+\left(\!\begin{smallmatrix}0 & -\bar{z}\phantom{}\\ z & 0\end{smallmatrix}\!\right)$ for ![]() $z\in \mathbb{H}$. In what follows, we call
$z\in \mathbb{H}$. In what follows, we call ![]() ${\rm\Omega}$ the Casimir operator.
${\rm\Omega}$ the Casimir operator.
2.3 Automorphic forms
For ![]() ${\it\lambda}\in \mathbb{C}$ and a discrete subgroup
${\it\lambda}\in \mathbb{C}$ and a discrete subgroup 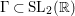 ${\rm\Gamma}\subset \text{SL}_{2}(\mathbb{R})$ we denote by
${\rm\Gamma}\subset \text{SL}_{2}(\mathbb{R})$ we denote by ![]() $S({\rm\Gamma},{\it\lambda})$ the space of Maass cusp forms of weight
$S({\rm\Gamma},{\it\lambda})$ the space of Maass cusp forms of weight ![]() $0$ on the complex upper half plane
$0$ on the complex upper half plane ![]() $\mathfrak{h}$ whose eigenvalue with respect to the hyperbolic Laplacian is
$\mathfrak{h}$ whose eigenvalue with respect to the hyperbolic Laplacian is ![]() $-{\it\lambda}$.
$-{\it\lambda}$.
For a discrete subgroup 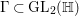 ${\rm\Gamma}\subset \text{GL}_{2}(\mathbb{H})$ and
${\rm\Gamma}\subset \text{GL}_{2}(\mathbb{H})$ and ![]() $r\in \mathbb{C}$ we denote by
$r\in \mathbb{C}$ we denote by 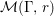 ${\mathcal{M}}({\rm\Gamma},r)$ the space of smooth functions
${\mathcal{M}}({\rm\Gamma},r)$ the space of smooth functions ![]() $F$ on
$F$ on 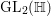 $\text{GL}_{2}(\mathbb{H})$ satisfying the following conditions:
$\text{GL}_{2}(\mathbb{H})$ satisfying the following conditions:
(1)
 ${\rm\Omega}\cdot F=-\frac{1}{2}(r^{2}/4+1)F$, where
${\rm\Omega}\cdot F=-\frac{1}{2}(r^{2}/4+1)F$, where  ${\rm\Omega}$ is the Casimir operator defined in (2.3);
${\rm\Omega}$ is the Casimir operator defined in (2.3);(2) for any
 $(z,{\it\gamma},g,k)\in Z^{+}\times {\rm\Gamma}\times G\times K$, we have
$(z,{\it\gamma},g,k)\in Z^{+}\times {\rm\Gamma}\times G\times K$, we have  $F(z{\it\gamma}gk)=F(g)$;
$F(z{\it\gamma}gk)=F(g)$;(3)
 $F$ is of moderate growth.
$F$ is of moderate growth.
Let ![]() $K_{{\it\alpha}}$, with
$K_{{\it\alpha}}$, with ![]() ${\it\alpha}\in \mathbb{C}$, denote the modified Bessel function (see [Reference Andrews, Askey and Roy1, §4.12]), which satisfies the differential equation
${\it\alpha}\in \mathbb{C}$, denote the modified Bessel function (see [Reference Andrews, Askey and Roy1, §4.12]), which satisfies the differential equation
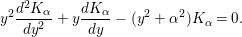 $$\begin{eqnarray}y^{2}\frac{d^{2}K_{{\it\alpha}}}{dy^{2}}+y\frac{dK_{{\it\alpha}}}{dy}-(y^{2}+{\it\alpha}^{2})K_{{\it\alpha}}=0.\end{eqnarray}$$
$$\begin{eqnarray}y^{2}\frac{d^{2}K_{{\it\alpha}}}{dy^{2}}+y\frac{dK_{{\it\alpha}}}{dy}-(y^{2}+{\it\alpha}^{2})K_{{\it\alpha}}=0.\end{eqnarray}$$Proposition 2.1. Let ![]() ${\rm\Gamma}$ be an arithmetic subgroup of
${\rm\Gamma}$ be an arithmetic subgroup of 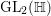 $\text{GL}_{2}(\mathbb{H})$, and let
$\text{GL}_{2}(\mathbb{H})$, and let 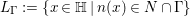 $L_{{\rm\Gamma}}:=\{x\in \mathbb{H}\mid n(x)\in N\cap {\rm\Gamma}\}$ and
$L_{{\rm\Gamma}}:=\{x\in \mathbb{H}\mid n(x)\in N\cap {\rm\Gamma}\}$ and ![]() $\hat{L_{{\rm\Gamma}}}$ be the dual lattice of
$\hat{L_{{\rm\Gamma}}}$ be the dual lattice of ![]() $L_{{\rm\Gamma}}$ with respect to
$L_{{\rm\Gamma}}$ with respect to ![]() $\operatorname{tr}$. Then
$\operatorname{tr}$. Then 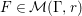 $F\in {\mathcal{M}}({\rm\Gamma},r)$ admits a Fourier expansion
$F\in {\mathcal{M}}({\rm\Gamma},r)$ admits a Fourier expansion
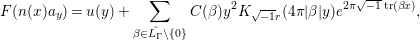 $$\begin{eqnarray}F(n(x)a_{y})=u(y)+\mathop{\sum }_{{\it\beta}\in \hat{L_{{\rm\Gamma}}}\setminus \{0\}}C({\it\beta})y^{2}K_{\sqrt{-1}r}(4{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{tr}({\it\beta}x)},\end{eqnarray}$$
$$\begin{eqnarray}F(n(x)a_{y})=u(y)+\mathop{\sum }_{{\it\beta}\in \hat{L_{{\rm\Gamma}}}\setminus \{0\}}C({\it\beta})y^{2}K_{\sqrt{-1}r}(4{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{tr}({\it\beta}x)},\end{eqnarray}$$ with a smooth function ![]() $u$ on
$u$ on ![]() $\mathbb{R}_{{>}0}$.
$\mathbb{R}_{{>}0}$.
Proof. A Maass form 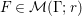 $F\in {\mathcal{M}}({\rm\Gamma};r)$ is left-invariant with respect to
$F\in {\mathcal{M}}({\rm\Gamma};r)$ is left-invariant with respect to 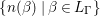 $\{n({\it\beta})\mid {\it\beta}\in L_{{\rm\Gamma}}\}$. This implies that
$\{n({\it\beta})\mid {\it\beta}\in L_{{\rm\Gamma}}\}$. This implies that 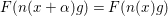 $F(n(x+{\it\alpha})g)=F(n(x)g)$ holds for
$F(n(x+{\it\alpha})g)=F(n(x)g)$ holds for ![]() ${\it\alpha}\in L_{{\rm\Gamma}}$ and
${\it\alpha}\in L_{{\rm\Gamma}}$ and ![]() $g\in G$. Therefore,
$g\in G$. Therefore, ![]() $F$ has an expansion
$F$ has an expansion
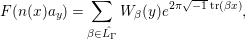 $$\begin{eqnarray}F(n(x)a_{y})=\mathop{\sum }_{{\it\beta}\in \hat{L_{{\rm\Gamma}}}}W_{{\it\beta}}(y)e^{2{\it\pi}\sqrt{-1}\operatorname{tr}({\it\beta}x)},\end{eqnarray}$$
$$\begin{eqnarray}F(n(x)a_{y})=\mathop{\sum }_{{\it\beta}\in \hat{L_{{\rm\Gamma}}}}W_{{\it\beta}}(y)e^{2{\it\pi}\sqrt{-1}\operatorname{tr}({\it\beta}x)},\end{eqnarray}$$ with a smooth function ![]() $W_{{\it\beta}}$ on
$W_{{\it\beta}}$ on ![]() $\mathbb{R}_{+}^{\times }$. For
$\mathbb{R}_{+}^{\times }$. For 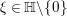 ${\it\xi}\in \mathbb{H}\setminus \{0\}$ we put
${\it\xi}\in \mathbb{H}\setminus \{0\}$ we put 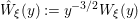 ${\hat{W}}_{{\it\xi}}(y):=y^{-3/2}W_{{\it\xi}}(y)$. From the condition
${\hat{W}}_{{\it\xi}}(y):=y^{-3/2}W_{{\it\xi}}(y)$. From the condition 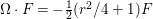 ${\rm\Omega}\cdot F=-\frac{1}{2}(r^{2}/4+1)F$ we deduce that
${\rm\Omega}\cdot F=-\frac{1}{2}(r^{2}/4+1)F$ we deduce that ![]() ${\hat{W}}_{{\it\beta}}$ satisfies the differential equation
${\hat{W}}_{{\it\beta}}$ satisfies the differential equation
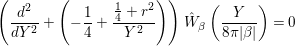 $$\begin{eqnarray}\left(\frac{d^{2}}{dY^{2}}+\left(-\frac{1}{4}+\frac{\frac{1}{4}+r^{2}}{Y^{2}}\right)\right){\hat{W}}_{{\it\beta}}\left(\frac{Y}{8{\it\pi}|{\it\beta}|}\right)=0\end{eqnarray}$$
$$\begin{eqnarray}\left(\frac{d^{2}}{dY^{2}}+\left(-\frac{1}{4}+\frac{\frac{1}{4}+r^{2}}{Y^{2}}\right)\right){\hat{W}}_{{\it\beta}}\left(\frac{Y}{8{\it\pi}|{\it\beta}|}\right)=0\end{eqnarray}$$ for 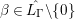 ${\it\beta}\in \hat{L_{{\rm\Gamma}}}\setminus \{0\}$, where
${\it\beta}\in \hat{L_{{\rm\Gamma}}}\setminus \{0\}$, where 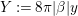 $Y:=8{\it\pi}|{\it\beta}|y$. This is precisely the differential equation for the Whittaker function (see [Reference Andrews, Askey and Roy1, §4.3]). With the Whittaker function
$Y:=8{\it\pi}|{\it\beta}|y$. This is precisely the differential equation for the Whittaker function (see [Reference Andrews, Askey and Roy1, §4.3]). With the Whittaker function 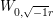 $W_{0,\sqrt{-1}r}$ parametrized by
$W_{0,\sqrt{-1}r}$ parametrized by 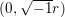 $(0,\sqrt{-1}r)$ we thereby see that
$(0,\sqrt{-1}r)$ we thereby see that
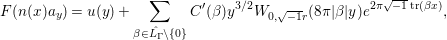 $$\begin{eqnarray}F(n(x)a_{y})=u(y)+\mathop{\sum }_{{\it\beta}\in \hat{L_{{\rm\Gamma}}}\setminus \{0\}}C^{\prime }({\it\beta})y^{3/2}W_{0,\sqrt{-1}r}(8{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{tr}({\it\beta}x)},\end{eqnarray}$$
$$\begin{eqnarray}F(n(x)a_{y})=u(y)+\mathop{\sum }_{{\it\beta}\in \hat{L_{{\rm\Gamma}}}\setminus \{0\}}C^{\prime }({\it\beta})y^{3/2}W_{0,\sqrt{-1}r}(8{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{tr}({\it\beta}x)},\end{eqnarray}$$ with constants ![]() $C^{\prime }({\it\beta})$ depending only on
$C^{\prime }({\it\beta})$ depending only on ![]() ${\it\beta}$. We now note the relation
${\it\beta}$. We now note the relation
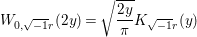 $$\begin{eqnarray}W_{0,\sqrt{-1}r}(2y)=\sqrt{\frac{2y}{{\it\pi}}}K_{\sqrt{-1}r}(y)\end{eqnarray}$$
$$\begin{eqnarray}W_{0,\sqrt{-1}r}(2y)=\sqrt{\frac{2y}{{\it\pi}}}K_{\sqrt{-1}r}(y)\end{eqnarray}$$ (see [Reference Oliver, Lozier, Boisvert and Clark21, §13, 13.18(iii), 13.18.9]). This means that ![]() $F$ has the Fourier expansion as in the statement of the proposition.◻
$F$ has the Fourier expansion as in the statement of the proposition.◻
We consider the automorphic forms above with specified discrete subgroups of ![]() $\text{SL}_{2}(\mathbb{R})$ and
$\text{SL}_{2}(\mathbb{R})$ and  $\text{GL}_{2}(\mathbb{H})$. As a discrete subgroup of
$\text{GL}_{2}(\mathbb{H})$. As a discrete subgroup of ![]() $\text{SL}_{2}(\mathbb{R})$ we take the congruence subgroup
$\text{SL}_{2}(\mathbb{R})$ we take the congruence subgroup ![]() ${\rm\Gamma}_{0}(2)$ of level
${\rm\Gamma}_{0}(2)$ of level ![]() $2$. For a choice of a discrete subgroup of
$2$. For a choice of a discrete subgroup of  $\text{GL}_{2}(\mathbb{H})$ we recall that
$\text{GL}_{2}(\mathbb{H})$ we recall that ![]() $B$ denotes the definite quaternion algebra over
$B$ denotes the definite quaternion algebra over ![]() $\mathbb{Q}$ with discriminant
$\mathbb{Q}$ with discriminant ![]() $d_{B}=2$. Up to
$d_{B}=2$. Up to ![]() $B^{\times }$-conjugation this has a unique maximal order. In fact, we have the maximal order
$B^{\times }$-conjugation this has a unique maximal order. In fact, we have the maximal order ![]() ${\mathcal{O}}$ given by
${\mathcal{O}}$ given by
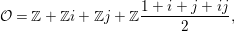 $$\begin{eqnarray}{\mathcal{O}}=\mathbb{Z}+\mathbb{Z}i+\mathbb{Z}j+\mathbb{Z}\frac{1+i+j+ij}{2},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}=\mathbb{Z}+\mathbb{Z}i+\mathbb{Z}j+\mathbb{Z}\frac{1+i+j+ij}{2},\end{eqnarray}$$ which is called the Hurwitz order. As a discrete subgroup of 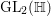 $\text{GL}_{2}(\mathbb{H})$ we take
$\text{GL}_{2}(\mathbb{H})$ we take 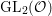 $\text{GL}_{2}({\mathcal{O}})$.
$\text{GL}_{2}({\mathcal{O}})$.
Proposition 2.2. The group 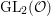 $\text{GL}_{2}({\mathcal{O}})$ is generated by
$\text{GL}_{2}({\mathcal{O}})$ is generated by
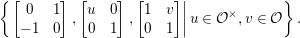 $$\begin{eqnarray}\left\{\left.\left[\begin{array}{@{}cc@{}}0 & 1\\ -1 & 0\end{array}\right],\left[\begin{array}{@{}cc@{}}u & 0\\ 0 & 1\end{array}\right],\left[\begin{array}{@{}cc@{}}1 & v\\ 0 & 1\end{array}\right]\right|u\in {\mathcal{O}}^{\times },v\in {\mathcal{O}}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\left.\left[\begin{array}{@{}cc@{}}0 & 1\\ -1 & 0\end{array}\right],\left[\begin{array}{@{}cc@{}}u & 0\\ 0 & 1\end{array}\right],\left[\begin{array}{@{}cc@{}}1 & v\\ 0 & 1\end{array}\right]\right|u\in {\mathcal{O}}^{\times },v\in {\mathcal{O}}\right\}.\end{eqnarray}$$Proof. Any element of the form 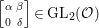 $\left[\!\begin{smallmatrix}{\it\alpha} & {\it\beta}\phantom{}\\ 0 & {\it\delta}\end{smallmatrix}\!\right]\in \text{GL}_{2}({\mathcal{O}})$ can be expressed as
$\left[\!\begin{smallmatrix}{\it\alpha} & {\it\beta}\phantom{}\\ 0 & {\it\delta}\end{smallmatrix}\!\right]\in \text{GL}_{2}({\mathcal{O}})$ can be expressed as
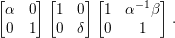 $$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}{\it\alpha} & 0\\ 0 & 1\end{array}\right]\left[\begin{array}{@{}cc@{}}1 & 0\\ 0 & {\it\delta}\end{array}\right]\left[\begin{array}{@{}cc@{}}1 & {\it\alpha}^{-1}{\it\beta}\\ 0 & 1\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}{\it\alpha} & 0\\ 0 & 1\end{array}\right]\left[\begin{array}{@{}cc@{}}1 & 0\\ 0 & {\it\delta}\end{array}\right]\left[\begin{array}{@{}cc@{}}1 & {\it\alpha}^{-1}{\it\beta}\\ 0 & 1\end{array}\right].\end{eqnarray}$$ We see that 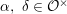 ${\it\alpha},~{\it\delta}\in {\mathcal{O}}^{\times }$, and thus
${\it\alpha},~{\it\delta}\in {\mathcal{O}}^{\times }$, and thus 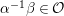 ${\it\alpha}^{-1}{\it\beta}\in {\mathcal{O}}$. We note that
${\it\alpha}^{-1}{\it\beta}\in {\mathcal{O}}$. We note that
 $$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}0 & 1\\ -1 & 0\end{array}\right]\left[\begin{array}{@{}cc@{}}u & 0\\ 0 & 1\end{array}\right]\left[\begin{array}{@{}cc@{}}0 & -1\\ 1 & 0\end{array}\right]=\left[\begin{array}{@{}cc@{}}1 & 0\\ 0 & u\end{array}\right],\quad \left[\begin{array}{@{}cc@{}}0 & 1\\ -1 & 0\end{array}\right]^{3}=\left[\begin{array}{@{}cc@{}}0 & -1\\ 1 & 0\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}0 & 1\\ -1 & 0\end{array}\right]\left[\begin{array}{@{}cc@{}}u & 0\\ 0 & 1\end{array}\right]\left[\begin{array}{@{}cc@{}}0 & -1\\ 1 & 0\end{array}\right]=\left[\begin{array}{@{}cc@{}}1 & 0\\ 0 & u\end{array}\right],\quad \left[\begin{array}{@{}cc@{}}0 & 1\\ -1 & 0\end{array}\right]^{3}=\left[\begin{array}{@{}cc@{}}0 & -1\\ 1 & 0\end{array}\right].\end{eqnarray}$$ These imply the assertion for 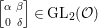 $\left[\!\begin{smallmatrix}{\it\alpha} & {\it\beta}\phantom{}\\ 0 & {\it\delta}\end{smallmatrix}\!\right]\in \text{GL}_{2}({\mathcal{O}})$. Next, we have the following claim.
$\left[\!\begin{smallmatrix}{\it\alpha} & {\it\beta}\phantom{}\\ 0 & {\it\delta}\end{smallmatrix}\!\right]\in \text{GL}_{2}({\mathcal{O}})$. Next, we have the following claim.
For 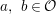 $a,~b\in {\mathcal{O}}$with
$a,~b\in {\mathcal{O}}$with ![]() $b\not =0$there exist
$b\not =0$there exist 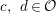 $c,~d\in {\mathcal{O}}$such that
$c,~d\in {\mathcal{O}}$such that  $a=cb+d,\quad {\it\nu}(d)<{\it\nu}(b)$. This follows from [Reference Krieg16, Chap. I, Section 1, Corollary 1.8]. This reduces the general case of
$a=cb+d,\quad {\it\nu}(d)<{\it\nu}(b)$. This follows from [Reference Krieg16, Chap. I, Section 1, Corollary 1.8]. This reduces the general case of 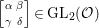 $\left[\!\begin{smallmatrix}{\it\alpha} & {\it\beta}\phantom{}\\ {\it\gamma} & {\it\delta}\end{smallmatrix}\!\right]\in \text{GL}_{2}({\mathcal{O}})$,
$\left[\!\begin{smallmatrix}{\it\alpha} & {\it\beta}\phantom{}\\ {\it\gamma} & {\it\delta}\end{smallmatrix}\!\right]\in \text{GL}_{2}({\mathcal{O}})$, ![]() ${\it\gamma}\not =0$, to the previous case. This completes the proof of the proposition.◻
${\it\gamma}\not =0$, to the previous case. This completes the proof of the proposition.◻
Let 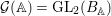 ${\mathcal{G}}(\mathbb{A})=\text{GL}_{2}(B_{\mathbb{A}})$, where
${\mathcal{G}}(\mathbb{A})=\text{GL}_{2}(B_{\mathbb{A}})$, where ![]() $B_{\mathbb{A}}$ denotes the adelization of
$B_{\mathbb{A}}$ denotes the adelization of ![]() $B$, and let
$B$, and let ![]() $U$ be the compact subgroup of
$U$ be the compact subgroup of ![]() ${\mathcal{G}}(\mathbb{A})$ given by
${\mathcal{G}}(\mathbb{A})$ given by 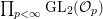 $\prod _{p<\infty }\text{GL}_{2}({\mathcal{O}}_{p})$, where
$\prod _{p<\infty }\text{GL}_{2}({\mathcal{O}}_{p})$, where ![]() ${\mathcal{O}}_{p}$ denotes the
${\mathcal{O}}_{p}$ denotes the ![]() $p$-adic completion of
$p$-adic completion of ![]() ${\mathcal{O}}$ at a finite prime
${\mathcal{O}}$ at a finite prime ![]() $p$. Then, the class number of
$p$. Then, the class number of ![]() ${\mathcal{G}}$ with respect to
${\mathcal{G}}$ with respect to ![]() $U$ is defined as the number of cosets in
$U$ is defined as the number of cosets in 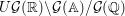 $U{\mathcal{G}}(\mathbb{R})\setminus {\mathcal{G}}(\mathbb{A})/{\mathcal{G}}(\mathbb{Q})$.
$U{\mathcal{G}}(\mathbb{R})\setminus {\mathcal{G}}(\mathbb{A})/{\mathcal{G}}(\mathbb{Q})$.
We next put ![]() ${\mathcal{P}}$ to be a standard
${\mathcal{P}}$ to be a standard ![]() $\mathbb{Q}$-parabolic subgroup of
$\mathbb{Q}$-parabolic subgroup of ![]() ${\mathcal{G}}$ whose group of
${\mathcal{G}}$ whose group of ![]() $\mathbb{Q}$-rational points is
$\mathbb{Q}$-rational points is 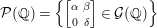 ${\mathcal{P}}(\mathbb{Q})=\left\{\left[\!\begin{smallmatrix}{\it\alpha} & {\it\beta}\phantom{}\\ 0 & {\it\delta}\end{smallmatrix}\!\right]\in {\mathcal{G}}(\mathbb{Q})\right\}$. We now recall that, for an arithmetic subgroup
${\mathcal{P}}(\mathbb{Q})=\left\{\left[\!\begin{smallmatrix}{\it\alpha} & {\it\beta}\phantom{}\\ 0 & {\it\delta}\end{smallmatrix}\!\right]\in {\mathcal{G}}(\mathbb{Q})\right\}$. We now recall that, for an arithmetic subgroup 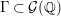 ${\rm\Gamma}\subset {\mathcal{G}}(\mathbb{Q})$, the cosets
${\rm\Gamma}\subset {\mathcal{G}}(\mathbb{Q})$, the cosets 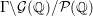 ${\rm\Gamma}\setminus {\mathcal{G}}(\mathbb{Q})/{\mathcal{P}}(\mathbb{Q})$ are called the set of
${\rm\Gamma}\setminus {\mathcal{G}}(\mathbb{Q})/{\mathcal{P}}(\mathbb{Q})$ are called the set of ![]() ${\rm\Gamma}$-cusps.
${\rm\Gamma}$-cusps.
(1) The class number of
 ${\mathcal{G}}$ with respect to
${\mathcal{G}}$ with respect to  $U$ is one, namely we have
$U$ is one, namely we have  ${\mathcal{G}}(\mathbb{A})={\mathcal{G}}(\mathbb{Q}){\mathcal{G}}(\mathbb{R})U$.
${\mathcal{G}}(\mathbb{A})={\mathcal{G}}(\mathbb{Q}){\mathcal{G}}(\mathbb{R})U$.(2) The number of cusps with respect to
 ${\rm\Gamma}:=\text{GL}_{2}({\mathcal{O}})$ is one.
${\rm\Gamma}:=\text{GL}_{2}({\mathcal{O}})$ is one.
Proof. According to [Reference Platonov and Rapinchuk24, Theorem 8.11] the class number of a reductive group over a number field ![]() $F$ is not greater than that of a parabolic
$F$ is not greater than that of a parabolic ![]() $F$-subgroup of it. Furthermore, the class number of a parabolic
$F$-subgroup of it. Furthermore, the class number of a parabolic ![]() $F$-subgroup is not greater than that of its Levi subgroup (see [Reference Platonov and Rapinchuk24, Proposition 5.4]). Hence, the class number of
$F$-subgroup is not greater than that of its Levi subgroup (see [Reference Platonov and Rapinchuk24, Proposition 5.4]). Hence, the class number of ![]() ${\mathcal{G}}$ with respect to
${\mathcal{G}}$ with respect to ![]() $U$ turns out to be not greater than that of the Levi subgroup
$U$ turns out to be not greater than that of the Levi subgroup ![]() ${\mathcal{L}}$ defined by the
${\mathcal{L}}$ defined by the ![]() $\mathbb{Q}$-rational points
$\mathbb{Q}$-rational points 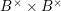 $B^{\times }\times B^{\times }$. Since the class number of
$B^{\times }\times B^{\times }$. Since the class number of ![]() $B^{\times }$ with respect to
$B^{\times }$ with respect to 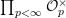 $\prod _{p<\infty }{\mathcal{O}}_{p}^{\times }$ is one, the class number of
$\prod _{p<\infty }{\mathcal{O}}_{p}^{\times }$ is one, the class number of ![]() ${\mathcal{G}}$ is also one, which means that
${\mathcal{G}}$ is also one, which means that 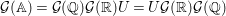 ${\mathcal{G}}(\mathbb{A})={\mathcal{G}}(\mathbb{Q}){\mathcal{G}}(\mathbb{R})U=U{\mathcal{G}}(\mathbb{R}){\mathcal{G}}(\mathbb{Q})$. This completes the proof of (1).
${\mathcal{G}}(\mathbb{A})={\mathcal{G}}(\mathbb{Q}){\mathcal{G}}(\mathbb{R})U=U{\mathcal{G}}(\mathbb{R}){\mathcal{G}}(\mathbb{Q})$. This completes the proof of (1).
The first assertion implies that there is a bijection
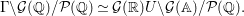 $$\begin{eqnarray}{\rm\Gamma}\setminus {\mathcal{G}}(\mathbb{Q})/{\mathcal{P}}(\mathbb{Q})\simeq {\mathcal{G}}(\mathbb{R})U\setminus {\mathcal{G}}(\mathbb{A})/{\mathcal{P}}(\mathbb{Q}).\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Gamma}\setminus {\mathcal{G}}(\mathbb{Q})/{\mathcal{P}}(\mathbb{Q})\simeq {\mathcal{G}}(\mathbb{R})U\setminus {\mathcal{G}}(\mathbb{A})/{\mathcal{P}}(\mathbb{Q}).\end{eqnarray}$$Furthermore, note an Iwasawa decomposition
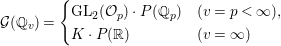 $$\begin{eqnarray}{\mathcal{G}}(\mathbb{Q}_{v})=\left\{\begin{array}{@{}ll@{}}\text{GL}_{2}({\mathcal{O}}_{p})\cdot P(\mathbb{Q}_{p})\quad & (v=p<\infty ),\\ K\cdot P(\mathbb{R})\quad & (v=\infty )\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{G}}(\mathbb{Q}_{v})=\left\{\begin{array}{@{}ll@{}}\text{GL}_{2}({\mathcal{O}}_{p})\cdot P(\mathbb{Q}_{p})\quad & (v=p<\infty ),\\ K\cdot P(\mathbb{R})\quad & (v=\infty )\end{array}\right.\end{eqnarray}$$ at every place ![]() $v\leqslant \infty$. We can then reduce the counting of the number of
$v\leqslant \infty$. We can then reduce the counting of the number of ![]() ${\rm\Gamma}$-cusps to that of the class number of the Levi subgroup
${\rm\Gamma}$-cusps to that of the class number of the Levi subgroup ![]() ${\mathcal{L}}$. This implies that the number of cusps with respect to
${\mathcal{L}}$. This implies that the number of cusps with respect to ![]() ${\rm\Gamma}$ is one, and completes the proof of the lemma.◻
${\rm\Gamma}$ is one, and completes the proof of the lemma.◻
We define ![]() ${\rm\Gamma}_{T}$ as a subgroup
${\rm\Gamma}_{T}$ as a subgroup 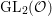 $\text{GL}_{2}({\mathcal{O}})$ generated by
$\text{GL}_{2}({\mathcal{O}})$ generated by
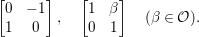 $$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}0 & -1\\ 1 & 0\end{array}\right],\quad \left[\begin{array}{@{}cc@{}}1 & {\it\beta}\\ 0 & 1\end{array}\right]\quad ({\it\beta}\in {\mathcal{O}}).\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}0 & -1\\ 1 & 0\end{array}\right],\quad \left[\begin{array}{@{}cc@{}}1 & {\it\beta}\\ 0 & 1\end{array}\right]\quad ({\it\beta}\in {\mathcal{O}}).\end{eqnarray}$$ In what follows, we deal mainly with 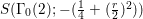 $S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+(\frac{r}{2})^{2}))$,
$S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+(\frac{r}{2})^{2}))$, 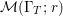 ${\mathcal{M}}({\rm\Gamma}_{T};r)$ and
${\mathcal{M}}({\rm\Gamma}_{T};r)$ and 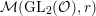 ${\mathcal{M}}(\text{GL}_{2}({\mathcal{O}}),r)$. For this we should note that the Selberg conjecture for
${\mathcal{M}}(\text{GL}_{2}({\mathcal{O}}),r)$. For this we should note that the Selberg conjecture for ![]() ${\rm\Gamma}_{0}(2)$ is verified (cf. [Reference Iwaniec12, Corollary 11.5]). This means the following.
${\rm\Gamma}_{0}(2)$ is verified (cf. [Reference Iwaniec12, Corollary 11.5]). This means the following.
Proposition 2.4. If 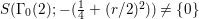 $S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+(r/2)^{2}))\not =\{0\}$, we have
$S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+(r/2)^{2}))\not =\{0\}$, we have 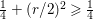 $\frac{1}{4}+(r/2)^{2}\geqslant \frac{1}{4}$, namely we can assume that
$\frac{1}{4}+(r/2)^{2}\geqslant \frac{1}{4}$, namely we can assume that ![]() $r\in \mathbb{R}$.
$r\in \mathbb{R}$.
By Proposition 2.1, the Fourier expansion of 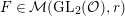 $F\in {\mathcal{M}}(\text{GL}_{2}({\mathcal{O}}),r)$ is then written as
$F\in {\mathcal{M}}(\text{GL}_{2}({\mathcal{O}}),r)$ is then written as
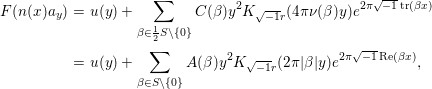 $$\begin{eqnarray}\displaystyle F(n(x)a_{y}) & = & \displaystyle u(y)+\mathop{\sum }_{{\it\beta}\in \frac{1}{2}S\setminus \{0\}}C({\it\beta})y^{2}K_{\sqrt{-1}r}(4{\it\pi}{\it\nu}({\it\beta})y)e^{2{\it\pi}\sqrt{-1}\operatorname{tr}({\it\beta}x)}\nonumber\\ \displaystyle & = & \displaystyle u(y)+\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}A({\it\beta})y^{2}K_{\sqrt{-1}r}(2{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{Re}({\it\beta}x)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(n(x)a_{y}) & = & \displaystyle u(y)+\mathop{\sum }_{{\it\beta}\in \frac{1}{2}S\setminus \{0\}}C({\it\beta})y^{2}K_{\sqrt{-1}r}(4{\it\pi}{\it\nu}({\it\beta})y)e^{2{\it\pi}\sqrt{-1}\operatorname{tr}({\it\beta}x)}\nonumber\\ \displaystyle & = & \displaystyle u(y)+\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}A({\it\beta})y^{2}K_{\sqrt{-1}r}(2{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{Re}({\it\beta}x)},\nonumber\end{eqnarray}$$ with a smooth function ![]() $u$ on
$u$ on ![]() $\mathbb{R}_{{>}0}$. Here,
$\mathbb{R}_{{>}0}$. Here,
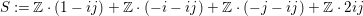 $$\begin{eqnarray}S:=\mathbb{Z}\cdot (1-ij)+\mathbb{Z}\cdot (-i-ij)+\mathbb{Z}\cdot (-j-ij)+\mathbb{Z}\cdot 2ij\end{eqnarray}$$
$$\begin{eqnarray}S:=\mathbb{Z}\cdot (1-ij)+\mathbb{Z}\cdot (-i-ij)+\mathbb{Z}\cdot (-j-ij)+\mathbb{Z}\cdot 2ij\end{eqnarray}$$ is the dual lattice of ![]() ${\mathcal{O}}$ with respect to the bilinear form on
${\mathcal{O}}$ with respect to the bilinear form on ![]() $\mathbb{H}\times \mathbb{H}$ defined by
$\mathbb{H}\times \mathbb{H}$ defined by 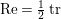 $\operatorname{Re}=\frac{1}{2}\operatorname{tr}$.
$\operatorname{Re}=\frac{1}{2}\operatorname{tr}$.
Now we introduce 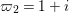 ${\it\varpi}_{2}=1+i$, which is a uniformizer of
${\it\varpi}_{2}=1+i$, which is a uniformizer of 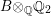 $B\otimes _{\mathbb{Q}}\mathbb{Q}_{2}$. We can verify the following lemma by a direct computation.
$B\otimes _{\mathbb{Q}}\mathbb{Q}_{2}$. We can verify the following lemma by a direct computation.
Lemma 2.5. We have 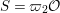 $S={\it\varpi}_{2}{\mathcal{O}}$.
$S={\it\varpi}_{2}{\mathcal{O}}$.
3 Some zeta integral of convolution type
In this section, we study certain zeta integrals which play a crucial role in the proof of automorphy in Section 4.
Theta functions
Consider the space of harmonic polynomials of degree ![]() $l$ on
$l$ on ![]() $\mathbb{H}$. These are homogeneous polynomials of degree
$\mathbb{H}$. These are homogeneous polynomials of degree ![]() $l$ and are annihilated by the Laplace operator in
$l$ and are annihilated by the Laplace operator in ![]() $4$ variables. We can act on this space by the cyclic group of order
$4$ variables. We can act on this space by the cyclic group of order ![]() $8$ generated by
$8$ generated by 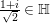 $\frac{1+i}{\sqrt{2}}\in \mathbb{H}$. Let
$\frac{1+i}{\sqrt{2}}\in \mathbb{H}$. Let ![]() $\{P_{l,{\it\nu}}\}_{{\it\nu}}$ denote a basis for this space consisting of eigenvectors under the above action. Hence,
$\{P_{l,{\it\nu}}\}_{{\it\nu}}$ denote a basis for this space consisting of eigenvectors under the above action. Hence,
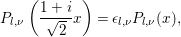 $$\begin{eqnarray}P_{l,{\it\nu}}\left(\frac{1+i}{\sqrt{2}}x\right)={\it\epsilon}_{l,{\it\nu}}P_{l,{\it\nu}}(x),\end{eqnarray}$$
$$\begin{eqnarray}P_{l,{\it\nu}}\left(\frac{1+i}{\sqrt{2}}x\right)={\it\epsilon}_{l,{\it\nu}}P_{l,{\it\nu}}(x),\end{eqnarray}$$ for some 8th root of unity ![]() ${\it\epsilon}_{l,v}$. Define the following theta function:
${\it\epsilon}_{l,v}$. Define the following theta function:
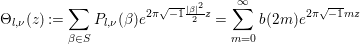 $$\begin{eqnarray}{\rm\Theta}_{l,{\it\nu}}(z):=\mathop{\sum }_{{\it\beta}\in S}P_{l,{\it\nu}}({\it\beta})e^{2{\it\pi}\sqrt{-1}\frac{|{\it\beta}|^{2}}{2}z}=\mathop{\sum }_{m=0}^{\infty }b(2m)e^{2{\it\pi}\sqrt{-1}mz}\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Theta}_{l,{\it\nu}}(z):=\mathop{\sum }_{{\it\beta}\in S}P_{l,{\it\nu}}({\it\beta})e^{2{\it\pi}\sqrt{-1}\frac{|{\it\beta}|^{2}}{2}z}=\mathop{\sum }_{m=0}^{\infty }b(2m)e^{2{\it\pi}\sqrt{-1}mz}\end{eqnarray}$$ on the complex upper half plane ![]() $\mathfrak{h}$, where
$\mathfrak{h}$, where 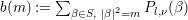 $b(m):=\sum _{{\it\beta}\in S,~|{\it\beta}|^{2}=m}P_{l,{\it\nu}}({\it\beta})$. Since
$b(m):=\sum _{{\it\beta}\in S,~|{\it\beta}|^{2}=m}P_{l,{\it\nu}}({\it\beta})$. Since ![]() $S$ is invariant under
$S$ is invariant under 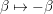 ${\it\beta}\mapsto -{\it\beta}$ and
${\it\beta}\mapsto -{\it\beta}$ and 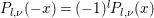 $P_{l,{\it\nu}}(-x)=(-1)^{l}P_{l,{\it\nu}}(x)$, we see that
$P_{l,{\it\nu}}(-x)=(-1)^{l}P_{l,{\it\nu}}(x)$, we see that ![]() ${\rm\Theta}_{l,{\it\nu}}(z)$ is the zero function if
${\rm\Theta}_{l,{\it\nu}}(z)$ is the zero function if ![]() $l$ is odd.
$l$ is odd.
Lemma 3.1. Let ![]() $l$ be an even nonnegative integer. Let
$l$ be an even nonnegative integer. Let ![]() ${\rm\Theta}_{l,{\it\nu}}$ be as defined in (3.2), with
${\rm\Theta}_{l,{\it\nu}}$ be as defined in (3.2), with ![]() $P_{l,{\it\nu}}$ satisfying (3.1). Then
$P_{l,{\it\nu}}$ satisfying (3.1). Then ![]() ${\rm\Theta}_{l,{\it\nu}}$ is a holomorphic modular form of weight
${\rm\Theta}_{l,{\it\nu}}$ is a holomorphic modular form of weight ![]() $l+2$ with respect to
$l+2$ with respect to ![]() ${\rm\Gamma}_{0}(2)$, and is a cusp form if
${\rm\Gamma}_{0}(2)$, and is a cusp form if ![]() $l\geqslant 2$. Moreover, we have the following transformation formula:
$l\geqslant 2$. Moreover, we have the following transformation formula:
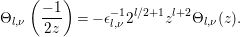 $$\begin{eqnarray}{\rm\Theta}_{l,{\it\nu}}\left(\frac{-1}{2z}\right)=-{\it\epsilon}_{l,{\it\nu}}^{-1}2^{l/2+1}z^{l+2}{\rm\Theta}_{l,{\it\nu}}(z).\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Theta}_{l,{\it\nu}}\left(\frac{-1}{2z}\right)=-{\it\epsilon}_{l,{\it\nu}}^{-1}2^{l/2+1}z^{l+2}{\rm\Theta}_{l,{\it\nu}}(z).\end{eqnarray}$$Proof. Set
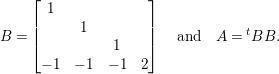 $$\begin{eqnarray}B=\left[\begin{array}{@{}cccc@{}}1\\ & 1\\ & & 1\\ -1 & -1 & -1 & 2\end{array}\right]\quad \text{and}\quad A=\text{}^{t}BB.\end{eqnarray}$$
$$\begin{eqnarray}B=\left[\begin{array}{@{}cccc@{}}1\\ & 1\\ & & 1\\ -1 & -1 & -1 & 2\end{array}\right]\quad \text{and}\quad A=\text{}^{t}BB.\end{eqnarray}$$ By (2.5), we see that the map 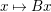 $x\mapsto Bx$ is a bijection from
$x\mapsto Bx$ is a bijection from 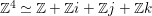 $\mathbb{Z}^{4}\simeq \mathbb{Z}+\mathbb{Z}i+\mathbb{Z}j+\mathbb{Z}k$ to
$\mathbb{Z}^{4}\simeq \mathbb{Z}+\mathbb{Z}i+\mathbb{Z}j+\mathbb{Z}k$ to 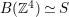 $B(\mathbb{Z}^{4})\simeq S$. Here, we consider
$B(\mathbb{Z}^{4})\simeq S$. Here, we consider ![]() $x$ as a column vector. For
$x$ as a column vector. For ![]() $P_{l,{\it\nu}}$ in the statement of the lemma, set
$P_{l,{\it\nu}}$ in the statement of the lemma, set 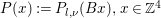 $P(x):=P_{l,{\it\nu}}(Bx),x\in \mathbb{Z}^{4}$. Then
$P(x):=P_{l,{\it\nu}}(Bx),x\in \mathbb{Z}^{4}$. Then ![]() $P$ is a homogeneous polynomial in
$P$ is a homogeneous polynomial in ![]() $4$ variables of degree
$4$ variables of degree ![]() $l$ annihilated by the operator
$l$ annihilated by the operator
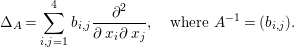 $$\begin{eqnarray}{\rm\Delta}_{A}=\mathop{\sum }_{i,j=1}^{4}b_{i,j}\frac{\partial ^{2}}{\partial \,x_{i}\partial \,x_{j}},\quad \text{where }A^{-1}=(b_{i,j}).\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}_{A}=\mathop{\sum }_{i,j=1}^{4}b_{i,j}\frac{\partial ^{2}}{\partial \,x_{i}\partial \,x_{j}},\quad \text{where }A^{-1}=(b_{i,j}).\end{eqnarray}$$ One can then see that 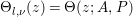 ${\rm\Theta}_{l,{\it\nu}}(z)={\rm\Theta}(z;A,P)$, where
${\rm\Theta}_{l,{\it\nu}}(z)={\rm\Theta}(z;A,P)$, where
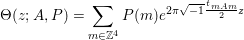 $$\begin{eqnarray}{\rm\Theta}(z;A,P)=\mathop{\sum }_{m\in \mathbb{Z}^{4}}P(m)e^{2{\it\pi}\sqrt{-1}\frac{\text{}^{t}mAm}{2}z}\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Theta}(z;A,P)=\mathop{\sum }_{m\in \mathbb{Z}^{4}}P(m)e^{2{\it\pi}\sqrt{-1}\frac{\text{}^{t}mAm}{2}z}\end{eqnarray}$$ is as defined in [Reference Miyake20, Corollary 4.9.5]. Since all diagonal entries of ![]() $A$ and
$A$ and ![]() $2A^{-1}$ are even, [Reference Miyake20, part (3) of Corollary 4.9.5] implies that
$2A^{-1}$ are even, [Reference Miyake20, part (3) of Corollary 4.9.5] implies that ![]() ${\rm\Theta}_{l,{\it\nu}}$ is a holomorphic modular form of weight
${\rm\Theta}_{l,{\it\nu}}$ is a holomorphic modular form of weight ![]() $l+2$ with respect to
$l+2$ with respect to ![]() ${\rm\Gamma}_{0}(2)$, and is a cusp form if
${\rm\Gamma}_{0}(2)$, and is a cusp form if ![]() $l\geqslant 2$. Once again, by [Reference Miyake20, part (3) of Corollary 4.9.5], we have
$l\geqslant 2$. Once again, by [Reference Miyake20, part (3) of Corollary 4.9.5], we have
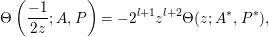 $$\begin{eqnarray}{\rm\Theta}\left(\frac{-1}{2z};A,P\right)=-2^{l+1}z^{l+2}{\rm\Theta}(z;A^{\ast },P^{\ast }),\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Theta}\left(\frac{-1}{2z};A,P\right)=-2^{l+1}z^{l+2}{\rm\Theta}(z;A^{\ast },P^{\ast }),\end{eqnarray}$$ where 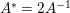 $A^{\ast }=2A^{-1}$ and
$A^{\ast }=2A^{-1}$ and 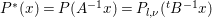 $P^{\ast }(x)=P(A^{-1}x)=P_{l,{\it\nu}}(\text{}^{t}B^{-1}x)$. Note that the map
$P^{\ast }(x)=P(A^{-1}x)=P_{l,{\it\nu}}(\text{}^{t}B^{-1}x)$. Note that the map 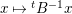 $x\mapsto \text{}^{t}B^{-1}x$ can be regarded as a bijection between
$x\mapsto \text{}^{t}B^{-1}x$ can be regarded as a bijection between ![]() $\mathbb{Z}^{4}$ and
$\mathbb{Z}^{4}$ and ![]() ${\mathcal{O}}$. Hence, we see that
${\mathcal{O}}$. Hence, we see that
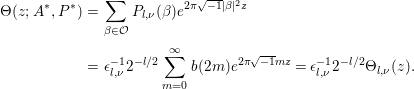 $$\begin{eqnarray}\displaystyle {\rm\Theta}(z;A^{\ast },P^{\ast }) & = & \displaystyle \mathop{\sum }_{{\it\beta}\in {\mathcal{O}}}P_{l,{\it\nu}}({\it\beta})e^{2{\it\pi}\sqrt{-1}|{\it\beta}|^{2}z}\nonumber\\ \displaystyle & = & \displaystyle {\it\epsilon}_{l,{\it\nu}}^{-1}2^{-l/2}\mathop{\sum }_{m=0}^{\infty }b(2m)e^{2{\it\pi}\sqrt{-1}mz}={\it\epsilon}_{l,{\it\nu}}^{-1}2^{-l/2}{\rm\Theta}_{l,{\it\nu}}(z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\rm\Theta}(z;A^{\ast },P^{\ast }) & = & \displaystyle \mathop{\sum }_{{\it\beta}\in {\mathcal{O}}}P_{l,{\it\nu}}({\it\beta})e^{2{\it\pi}\sqrt{-1}|{\it\beta}|^{2}z}\nonumber\\ \displaystyle & = & \displaystyle {\it\epsilon}_{l,{\it\nu}}^{-1}2^{-l/2}\mathop{\sum }_{m=0}^{\infty }b(2m)e^{2{\it\pi}\sqrt{-1}mz}={\it\epsilon}_{l,{\it\nu}}^{-1}2^{-l/2}{\rm\Theta}_{l,{\it\nu}}(z).\nonumber\end{eqnarray}$$Here, we have used Lemma 2.5 and (3.1). This completes the proof of the lemma.◻
Eisenstein series with respect to  ${\rm\Gamma}_{0}(2)$
${\rm\Gamma}_{0}(2)$
We introduce an Eisenstein series
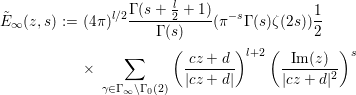 $$\begin{eqnarray}\displaystyle \tilde{E}_{\infty }(z,s) & := & \displaystyle (4{\it\pi})^{l/2}\frac{{\rm\Gamma}(s+\frac{l}{2}+1)}{{\rm\Gamma}(s)}({\it\pi}^{-s}{\rm\Gamma}(s){\it\zeta}(2s))\frac{1}{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{{\it\gamma}\in {\rm\Gamma}_{\infty }\setminus {\rm\Gamma}_{0}(2)}\left(\frac{cz+d}{|cz+d|}\right)^{l+2}\left(\frac{\operatorname{Im}(z)}{|cz+d|^{2}}\right)^{s}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{E}_{\infty }(z,s) & := & \displaystyle (4{\it\pi})^{l/2}\frac{{\rm\Gamma}(s+\frac{l}{2}+1)}{{\rm\Gamma}(s)}({\it\pi}^{-s}{\rm\Gamma}(s){\it\zeta}(2s))\frac{1}{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{{\it\gamma}\in {\rm\Gamma}_{\infty }\setminus {\rm\Gamma}_{0}(2)}\left(\frac{cz+d}{|cz+d|}\right)^{l+2}\left(\frac{\operatorname{Im}(z)}{|cz+d|^{2}}\right)^{s}\end{eqnarray}$$ on ![]() $\mathfrak{h}$ with a complex parameter
$\mathfrak{h}$ with a complex parameter ![]() $s$, where
$s$, where 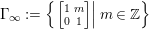 ${\rm\Gamma}_{\infty }:=\left\{\left.\left[\!\begin{smallmatrix}1 & m\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]\right|m\in \mathbb{Z}\right\}$. The Eisenstein series satisfies the following functional equation.
${\rm\Gamma}_{\infty }:=\left\{\left.\left[\!\begin{smallmatrix}1 & m\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]\right|m\in \mathbb{Z}\right\}$. The Eisenstein series satisfies the following functional equation.
Lemma 3.2. Let 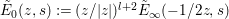 $\tilde{E}_{0}(z,s):=(z/|z|)^{l+2}\tilde{E}_{\infty }(-1/2z,s)$. Then the functional equation
$\tilde{E}_{0}(z,s):=(z/|z|)^{l+2}\tilde{E}_{\infty }(-1/2z,s)$. Then the functional equation
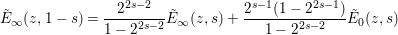 $$\begin{eqnarray}\tilde{E}_{\infty }(z,1-s)=\frac{2^{2s-2}}{1-2^{2s-2}}\tilde{E}_{\infty }(z,s)+\frac{2^{s-1}(1-2^{2s-1})}{1-2^{2s-2}}\tilde{E}_{0}(z,s)\end{eqnarray}$$
$$\begin{eqnarray}\tilde{E}_{\infty }(z,1-s)=\frac{2^{2s-2}}{1-2^{2s-2}}\tilde{E}_{\infty }(z,s)+\frac{2^{s-1}(1-2^{2s-1})}{1-2^{2s-2}}\tilde{E}_{0}(z,s)\end{eqnarray}$$holds.
Proof. This is settled by the argument in [Reference Duke and Imamoḡlu7, Lemma 7] with the help of the formula for the scattering matrices in [Reference Iwaniec12, §11.2]. ◻
Let 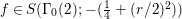 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+(r/2)^{2}))$ be an eigenfunction with respect to the Atkin–Lehner involution; that is,
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+(r/2)^{2}))$ be an eigenfunction with respect to the Atkin–Lehner involution; that is, 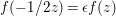 $f(-1/2z)={\it\epsilon}f(z)$ with some
$f(-1/2z)={\it\epsilon}f(z)$ with some 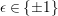 ${\it\epsilon}\in \{\pm 1\}$. Suppose the form
${\it\epsilon}\in \{\pm 1\}$. Suppose the form ![]() $f$ has the Fourier expansion
$f$ has the Fourier expansion
 $$\begin{eqnarray}f(x+\sqrt{-1}y)=\mathop{\sum }_{n\in \mathbb{Z}\setminus \{0\}}c(n)W_{0,\frac{\sqrt{-1}r}{2}}(4{\it\pi}|n|y)e^{2{\it\pi}\sqrt{-1}nx},\end{eqnarray}$$
$$\begin{eqnarray}f(x+\sqrt{-1}y)=\mathop{\sum }_{n\in \mathbb{Z}\setminus \{0\}}c(n)W_{0,\frac{\sqrt{-1}r}{2}}(4{\it\pi}|n|y)e^{2{\it\pi}\sqrt{-1}nx},\end{eqnarray}$$ where 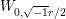 $W_{0,\sqrt{-1}r/2}$ denotes the Whittaker function with the parameter
$W_{0,\sqrt{-1}r/2}$ denotes the Whittaker function with the parameter 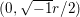 $(0,\sqrt{-1}r/2)$. Let
$(0,\sqrt{-1}r/2)$. Let ![]() $l$ be an even nonnegative integer. Let
$l$ be an even nonnegative integer. Let ![]() ${\rm\Theta}_{l,{\it\nu}}$ be as defined in (3.2), with
${\rm\Theta}_{l,{\it\nu}}$ be as defined in (3.2), with ![]() $P_{l,{\it\nu}}$ satisfying (3.1). Let
$P_{l,{\it\nu}}$ satisfying (3.1). Let 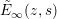 $\tilde{E}_{\infty }(z,s)$ be the Eisenstein series defined in (3.4). Let the zeta integral
$\tilde{E}_{\infty }(z,s)$ be the Eisenstein series defined in (3.4). Let the zeta integral ![]() $I(s)$ be defined by
$I(s)$ be defined by
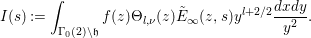 $$\begin{eqnarray}I(s):=\int _{{\rm\Gamma}_{0}(2)\setminus \mathfrak{h}}f(z){\rm\Theta}_{l,{\it\nu}}(z)\tilde{E}_{\infty }(z,s)y^{l+2/2}\frac{dxdy}{y^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}I(s):=\int _{{\rm\Gamma}_{0}(2)\setminus \mathfrak{h}}f(z){\rm\Theta}_{l,{\it\nu}}(z)\tilde{E}_{\infty }(z,s)y^{l+2/2}\frac{dxdy}{y^{2}}.\end{eqnarray}$$ A similar Rankin–Selberg integral was considered in [Reference Duke and Imamoḡlu7, Theorem 6] (see also [Reference Pitale22, (3.16)]). This integral is the main tool to prove the analytic properties of certain Dirichlet series associated with the lifting defined in Section 4. We would like to remark that the integral ![]() $I(s)$ is, in general, not Eulerian and does not represent an
$I(s)$ is, in general, not Eulerian and does not represent an ![]() $L$-function of
$L$-function of ![]() $f$.
$f$.
By Lemma 3.1, the above integral is well defined. Let us now state the theorem of this section.
Theorem 3.3. The zeta integral ![]() $I(s)$ is entire and is bounded on vertical strips. When
$I(s)$ is entire and is bounded on vertical strips. When 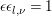 ${\it\epsilon}{\it\epsilon}_{l,{\it\nu}}=1$, we have
${\it\epsilon}{\it\epsilon}_{l,{\it\nu}}=1$, we have
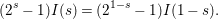 $$\begin{eqnarray}(2^{s}-1)I(s)=(2^{1-s}-1)I(1-s).\end{eqnarray}$$
$$\begin{eqnarray}(2^{s}-1)I(s)=(2^{1-s}-1)I(1-s).\end{eqnarray}$$ When 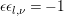 ${\it\epsilon}{\it\epsilon}_{l,{\it\nu}}=-1$, we have
${\it\epsilon}{\it\epsilon}_{l,{\it\nu}}=-1$, we have
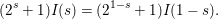 $$\begin{eqnarray}(2^{s}+1)I(s)=(2^{1-s}+1)I(1-s).\end{eqnarray}$$
$$\begin{eqnarray}(2^{s}+1)I(s)=(2^{1-s}+1)I(1-s).\end{eqnarray}$$Proof. The entireness and boundedness on vertical strips of ![]() $I(s)$ are verified by the same argument as [Reference Pitale22, §3.2]. We put
$I(s)$ are verified by the same argument as [Reference Pitale22, §3.2]. We put
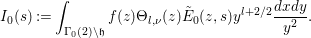 $$\begin{eqnarray}I_{0}(s):=\int _{{\rm\Gamma}_{0}(2)\setminus \mathfrak{h}}f(z){\rm\Theta}_{l,{\it\nu}}(z)\tilde{E}_{0}(z,s)y^{l+2/2}\frac{dxdy}{y^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}I_{0}(s):=\int _{{\rm\Gamma}_{0}(2)\setminus \mathfrak{h}}f(z){\rm\Theta}_{l,{\it\nu}}(z)\tilde{E}_{0}(z,s)y^{l+2/2}\frac{dxdy}{y^{2}}.\end{eqnarray}$$ Since ![]() ${\rm\Gamma}_{0}(2)$ is stable under conjugation by
${\rm\Gamma}_{0}(2)$ is stable under conjugation by  $\left[\begin{smallmatrix} & 1/\sqrt{2}\\ -\sqrt{2} & \end{smallmatrix}\right]\in \text{SL}_{2}(\mathbb{R})$, we can make a change of variable
$\left[\begin{smallmatrix} & 1/\sqrt{2}\\ -\sqrt{2} & \end{smallmatrix}\right]\in \text{SL}_{2}(\mathbb{R})$, we can make a change of variable  $z\mapsto -1/(2z)$. Now, using the assumption
$z\mapsto -1/(2z)$. Now, using the assumption 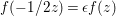 $f(-1/2z)={\it\epsilon}f(z)$, (3.3) and the definition of
$f(-1/2z)={\it\epsilon}f(z)$, (3.3) and the definition of 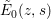 $\tilde{E}_{0}(z,s)$, we have
$\tilde{E}_{0}(z,s)$, we have
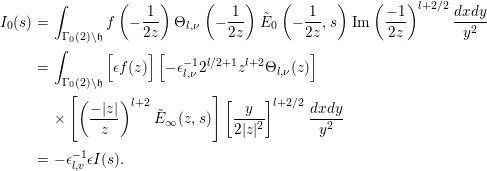 $$\begin{eqnarray}\displaystyle I_{0}(s) & = & \displaystyle \int _{{\rm\Gamma}_{0}(2)\setminus \mathfrak{h}}f\left(-\frac{1}{2z}\right){\rm\Theta}_{l,{\it\nu}}\left(-\frac{1}{2z}\right)\tilde{E}_{0}\left(-\frac{1}{2z},s\right)\text{Im}\left(\frac{-1}{2z}\right)^{l+2/2}\frac{dxdy}{y^{2}}\nonumber\\ \displaystyle & = & \displaystyle \int _{{\rm\Gamma}_{0}(2)\setminus \mathfrak{h}}\Big[{\it\epsilon}f(z)\Big]\left[-{\it\epsilon}_{l,{\it\nu}}^{-1}2^{l/2+1}z^{l+2}{\rm\Theta}_{l,{\it\nu}}(z)\right]\nonumber\\ \displaystyle & & \displaystyle \times \left[\left(\frac{-|z|}{z}\right)^{l+2}\tilde{E}_{\infty }(z,s)\right]\left[\frac{y}{2|z|^{2}}\right]^{l+2/2}\frac{dxdy}{y^{2}}\nonumber\\ \displaystyle & = & \displaystyle -{\it\epsilon}_{l,v}^{-1}{\it\epsilon}I(s).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{0}(s) & = & \displaystyle \int _{{\rm\Gamma}_{0}(2)\setminus \mathfrak{h}}f\left(-\frac{1}{2z}\right){\rm\Theta}_{l,{\it\nu}}\left(-\frac{1}{2z}\right)\tilde{E}_{0}\left(-\frac{1}{2z},s\right)\text{Im}\left(\frac{-1}{2z}\right)^{l+2/2}\frac{dxdy}{y^{2}}\nonumber\\ \displaystyle & = & \displaystyle \int _{{\rm\Gamma}_{0}(2)\setminus \mathfrak{h}}\Big[{\it\epsilon}f(z)\Big]\left[-{\it\epsilon}_{l,{\it\nu}}^{-1}2^{l/2+1}z^{l+2}{\rm\Theta}_{l,{\it\nu}}(z)\right]\nonumber\\ \displaystyle & & \displaystyle \times \left[\left(\frac{-|z|}{z}\right)^{l+2}\tilde{E}_{\infty }(z,s)\right]\left[\frac{y}{2|z|^{2}}\right]^{l+2/2}\frac{dxdy}{y^{2}}\nonumber\\ \displaystyle & = & \displaystyle -{\it\epsilon}_{l,v}^{-1}{\it\epsilon}I(s).\nonumber\end{eqnarray}$$From Lemma 3.2, we deduce
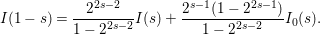 $$\begin{eqnarray}I(1-s)=\frac{2^{2s-2}}{1-2^{2s-2}}I(s)+\frac{2^{s-1}(1-2^{2s-1})}{1-2^{2s-2}}I_{0}(s).\end{eqnarray}$$
$$\begin{eqnarray}I(1-s)=\frac{2^{2s-2}}{1-2^{2s-2}}I(s)+\frac{2^{s-1}(1-2^{2s-1})}{1-2^{2s-2}}I_{0}(s).\end{eqnarray}$$Observe that
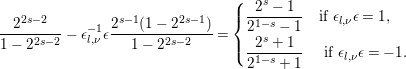 $$\begin{eqnarray}\frac{2^{2s-2}}{1-2^{2s-2}}-{\it\epsilon}_{l,{\it\nu}}^{-1}{\it\epsilon}\frac{2^{s-1}(1-2^{2s-1})}{1-2^{2s-2}}=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{2^{s}-1}{2^{1-s}-1}\quad & \text{if }{\it\epsilon}_{l,{\it\nu}}{\it\epsilon}=1,\\ \displaystyle \frac{2^{s}+1}{2^{1-s}+1}\quad & \text{ if }{\it\epsilon}_{l,{\it\nu}}{\it\epsilon}=-1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2^{2s-2}}{1-2^{2s-2}}-{\it\epsilon}_{l,{\it\nu}}^{-1}{\it\epsilon}\frac{2^{s-1}(1-2^{2s-1})}{1-2^{2s-2}}=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{2^{s}-1}{2^{1-s}-1}\quad & \text{if }{\it\epsilon}_{l,{\it\nu}}{\it\epsilon}=1,\\ \displaystyle \frac{2^{s}+1}{2^{1-s}+1}\quad & \text{ if }{\it\epsilon}_{l,{\it\nu}}{\it\epsilon}=-1.\end{array}\right.\end{eqnarray}$$We have therefore proved the theorem. ◻
4 Construction of the lifting
We now construct a lifting map from 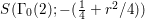 $S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ to
$S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ to 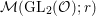 ${\mathcal{M}}(\text{GL}_{2}({\mathcal{O}});r)$, which is an analog of that of Pitale [Reference Pitale22]. The fundamental tool of our study is the converse theorem by Maass [Reference Maass19].
${\mathcal{M}}(\text{GL}_{2}({\mathcal{O}});r)$, which is an analog of that of Pitale [Reference Pitale22]. The fundamental tool of our study is the converse theorem by Maass [Reference Maass19].
Theorem 4.1. (Maass)
Let 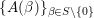 $\{A({\it\beta})\}_{{\it\beta}\in S\setminus \{0\}}$ be a sequence of complex numbers such that
$\{A({\it\beta})\}_{{\it\beta}\in S\setminus \{0\}}$ be a sequence of complex numbers such that
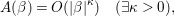 $$\begin{eqnarray}A({\it\beta})=O(|{\it\beta}|^{{\it\kappa}})\quad (\exists {\it\kappa}>0),\end{eqnarray}$$
$$\begin{eqnarray}A({\it\beta})=O(|{\it\beta}|^{{\it\kappa}})\quad (\exists {\it\kappa}>0),\end{eqnarray}$$and put
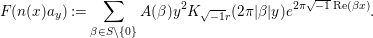 $$\begin{eqnarray}F(n(x)a_{y}):=\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}A({\it\beta})y^{2}K_{\sqrt{-1}r}(2{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{Re}({\it\beta}x)}.\end{eqnarray}$$
$$\begin{eqnarray}F(n(x)a_{y}):=\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}A({\it\beta})y^{2}K_{\sqrt{-1}r}(2{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{Re}({\it\beta}x)}.\end{eqnarray}$$ For a harmonic polynomial ![]() $P$ on
$P$ on ![]() $\mathbb{H}$ of degree
$\mathbb{H}$ of degree ![]() $l$ we introduce
$l$ we introduce
 $$\begin{eqnarray}{\it\xi}(s,P):={\it\pi}^{-2s}{\rm\Gamma}\left(s+\frac{\sqrt{-1}r}{2}\right){\rm\Gamma}\left(s-\frac{\sqrt{-1}r}{2}\right)\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}A({\it\beta})\frac{P({\it\beta})}{|{\it\beta}|^{2s}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\xi}(s,P):={\it\pi}^{-2s}{\rm\Gamma}\left(s+\frac{\sqrt{-1}r}{2}\right){\rm\Gamma}\left(s-\frac{\sqrt{-1}r}{2}\right)\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}A({\it\beta})\frac{P({\it\beta})}{|{\it\beta}|^{2s}},\end{eqnarray}$$ which converges for 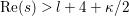 $\operatorname{Re}(s)>l+4+{\it\kappa}/2$. Let
$\operatorname{Re}(s)>l+4+{\it\kappa}/2$. Let ![]() $\{P_{l,{\it\nu}}\}_{{\it\nu}}$ be a basis of harmonic polynomials on
$\{P_{l,{\it\nu}}\}_{{\it\nu}}$ be a basis of harmonic polynomials on ![]() $\mathbb{H}$ of degree
$\mathbb{H}$ of degree ![]() $l$.
$l$.
Then 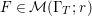 $F\in {\mathcal{M}}({\rm\Gamma}_{T};r)$ is equivalent to the condition that, for any
$F\in {\mathcal{M}}({\rm\Gamma}_{T};r)$ is equivalent to the condition that, for any ![]() $l,{\it\nu}$, the
$l,{\it\nu}$, the 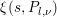 ${\it\xi}(s,P_{l,{\it\nu}})$ satisfies the following three conditions.
${\it\xi}(s,P_{l,{\it\nu}})$ satisfies the following three conditions.
(1) It has analytic continuation to the whole complex plane.
(2) It is bounded on any vertical strip of the complex plane.
(3) The functional equation
holds, where $$\begin{eqnarray}{\it\xi}(2+l-s,P_{l,{\it\nu}})=(-1)^{l}{\it\xi}(s,\hat{P}_{l,{\it\nu}})\end{eqnarray}$$
$$\begin{eqnarray}{\it\xi}(2+l-s,P_{l,{\it\nu}})=(-1)^{l}{\it\xi}(s,\hat{P}_{l,{\it\nu}})\end{eqnarray}$$ $\hat{P}(x):=P(\bar{x})$ for
$\hat{P}(x):=P(\bar{x})$ for  $x\in \mathbb{H}$.
$x\in \mathbb{H}$.
Recall that ![]() ${\rm\Gamma}_{T}$ is defined in (2.4). For this theorem we remark that the infinitesimal action of the Casimir operator
${\rm\Gamma}_{T}$ is defined in (2.4). For this theorem we remark that the infinitesimal action of the Casimir operator ![]() ${\rm\Omega}$ on the space of smooth right
${\rm\Omega}$ on the space of smooth right ![]() $K$-invariant functions on
$K$-invariant functions on ![]() $G/Z$ can be identified with a constant multiple of the hyperbolic Laplacian on
$G/Z$ can be identified with a constant multiple of the hyperbolic Laplacian on 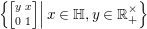 $\left\{\left.\!\left[\!\begin{smallmatrix}y & x\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]\right|x\in \mathbb{H},y\in \mathbb{R}_{+}^{\times }\right\}$ (for the hyperbolic Laplacian, see [Reference Maass19, (3)]). We can therefore follow the argument in [Reference Maass19, §2] to see that this theorem is useful also for our situation.
$\left\{\left.\!\left[\!\begin{smallmatrix}y & x\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]\right|x\in \mathbb{H},y\in \mathbb{R}_{+}^{\times }\right\}$ (for the hyperbolic Laplacian, see [Reference Maass19, (3)]). We can therefore follow the argument in [Reference Maass19, §2] to see that this theorem is useful also for our situation.
We wish to define 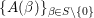 $\{A({\it\beta})\}_{{\it\beta}\in S\setminus \{0\}}$ from Fourier coefficients
$\{A({\it\beta})\}_{{\it\beta}\in S\setminus \{0\}}$ from Fourier coefficients ![]() $c(n)$ of
$c(n)$ of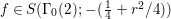 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$. Let
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$. Let 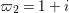 ${\it\varpi}_{2}=1+i$, as before. An easy computation shows that
${\it\varpi}_{2}=1+i$, as before. An easy computation shows that 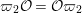 ${\it\varpi}_{2}{\mathcal{O}}={\mathcal{O}}{\it\varpi}_{2}$. This allows us to write any
${\it\varpi}_{2}{\mathcal{O}}={\mathcal{O}}{\it\varpi}_{2}$. This allows us to write any ![]() ${\it\beta}\in {\mathcal{O}}$ uniquely as
${\it\beta}\in {\mathcal{O}}$ uniquely as 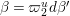 ${\it\beta}={\it\varpi}_{2}^{u}d{\it\beta}^{\prime }$, where
${\it\beta}={\it\varpi}_{2}^{u}d{\it\beta}^{\prime }$, where ![]() $u\geqslant 0$,
$u\geqslant 0$, ![]() $d$ is an odd integer and
$d$ is an odd integer and ![]() ${\it\beta}^{\prime }\in {\mathcal{O}}$ is neither of the form
${\it\beta}^{\prime }\in {\mathcal{O}}$ is neither of the form ![]() ${\it\varpi}_{2}{\it\beta}_{0}^{\prime }$ with some nonzero
${\it\varpi}_{2}{\it\beta}_{0}^{\prime }$ with some nonzero ![]() ${\it\beta}_{0}^{\prime }\in {\mathcal{O}}$ nor a multiple of an element of
${\it\beta}_{0}^{\prime }\in {\mathcal{O}}$ nor a multiple of an element of ![]() ${\mathcal{O}}$ by an odd integer. Hence, we can define
${\mathcal{O}}$ by an odd integer. Hence, we can define ![]() ${\it\varpi}_{2}^{m}|{\it\beta}$ by
${\it\varpi}_{2}^{m}|{\it\beta}$ by ![]() $m\leqslant u$ with
$m\leqslant u$ with ![]() $u$ as above. Recall that, by Lemma 2.5, we have
$u$ as above. Recall that, by Lemma 2.5, we have 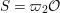 $S={\it\varpi}_{2}{\mathcal{O}}$. It thus makes sense to define the set
$S={\it\varpi}_{2}{\mathcal{O}}$. It thus makes sense to define the set ![]() $S^{\text{prim}}$ of primitive elements in
$S^{\text{prim}}$ of primitive elements in ![]() $S$ by
$S$ by
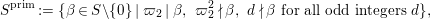 $$\begin{eqnarray}S^{\text{prim}}:=\{{\it\beta}\in S\setminus \{0\}\mid {\it\varpi}_{2}\mid {\it\beta},~{\it\varpi}_{2}^{2}\nmid {\it\beta},~d\nmid {\it\beta}~\text{for all odd integers }d\},\end{eqnarray}$$
$$\begin{eqnarray}S^{\text{prim}}:=\{{\it\beta}\in S\setminus \{0\}\mid {\it\varpi}_{2}\mid {\it\beta},~{\it\varpi}_{2}^{2}\nmid {\it\beta},~d\nmid {\it\beta}~\text{for all odd integers }d\},\end{eqnarray}$$ where ![]() $d\nmid {\it\beta}$ for
$d\nmid {\it\beta}$ for ![]() $d\in \mathbb{Z}$ means that
$d\in \mathbb{Z}$ means that ![]() ${\it\beta}$ is not a multiple of an element in
${\it\beta}$ is not a multiple of an element in ![]() $S$ by
$S$ by ![]() $d$.
$d$.
Proposition 4.2. Let 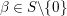 ${\it\beta}\in S\setminus \{0\}$ be expressed as
${\it\beta}\in S\setminus \{0\}$ be expressed as
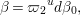 $$\begin{eqnarray}{\it\beta}={{\it\varpi}_{2}}^{u}d{\it\beta}_{0},\end{eqnarray}$$
$$\begin{eqnarray}{\it\beta}={{\it\varpi}_{2}}^{u}d{\it\beta}_{0},\end{eqnarray}$$ where ![]() $u$ is a nonnegative integer,
$u$ is a nonnegative integer, ![]() $d$ is an odd integer and
$d$ is an odd integer and 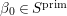 ${\it\beta}_{0}\in S^{\text{prim}}$. Given
${\it\beta}_{0}\in S^{\text{prim}}$. Given 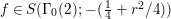 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ with Fourier coefficients
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ with Fourier coefficients ![]() $c(n)$ and eigenvalue
$c(n)$ and eigenvalue 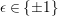 ${\it\epsilon}\in \{\pm 1\}$ of the Atkin–Lehner involution, we set
${\it\epsilon}\in \{\pm 1\}$ of the Atkin–Lehner involution, we set
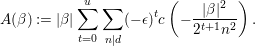 $$\begin{eqnarray}A({\it\beta}):=|{\it\beta}|\mathop{\sum }_{t=0}^{u}\mathop{\sum }_{n|d}(-{\it\epsilon})^{t}c\left(-\frac{|{\it\beta}|^{2}}{2^{t+1}n^{2}}\right).\end{eqnarray}$$
$$\begin{eqnarray}A({\it\beta}):=|{\it\beta}|\mathop{\sum }_{t=0}^{u}\mathop{\sum }_{n|d}(-{\it\epsilon})^{t}c\left(-\frac{|{\it\beta}|^{2}}{2^{t+1}n^{2}}\right).\end{eqnarray}$$ Let ![]() $\{P_{l,{\it\nu}}\}_{{\it\nu}}$ be a basis of harmonic polynomials on
$\{P_{l,{\it\nu}}\}_{{\it\nu}}$ be a basis of harmonic polynomials on ![]() $\mathbb{H}$ of degree
$\mathbb{H}$ of degree ![]() $l$ satisfying (3.1). Then we have
$l$ satisfying (3.1). Then we have
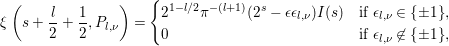 $$\begin{eqnarray}{\it\xi}\left(s+\frac{l}{2}+\frac{1}{2},P_{l,{\it\nu}}\right)=\left\{\begin{array}{@{}ll@{}}2^{1-l/2}{\it\pi}^{-(l+1)}(2^{s}-{\it\epsilon}{\it\epsilon}_{l,{\it\nu}})I(s)\quad & \text{if }{\it\epsilon}_{l,{\it\nu}}\in \{\pm 1\},\\ 0\quad & \text{if }{\it\epsilon}_{l,{\it\nu}}\not \in \{\pm 1\},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\it\xi}\left(s+\frac{l}{2}+\frac{1}{2},P_{l,{\it\nu}}\right)=\left\{\begin{array}{@{}ll@{}}2^{1-l/2}{\it\pi}^{-(l+1)}(2^{s}-{\it\epsilon}{\it\epsilon}_{l,{\it\nu}})I(s)\quad & \text{if }{\it\epsilon}_{l,{\it\nu}}\in \{\pm 1\},\\ 0\quad & \text{if }{\it\epsilon}_{l,{\it\nu}}\not \in \{\pm 1\},\end{array}\right.\end{eqnarray}$$ and the 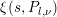 ${\it\xi}(s,P_{l,{\it\nu}})$ satisfies the three analytic conditions in Theorem 4.1.
${\it\xi}(s,P_{l,{\it\nu}})$ satisfies the three analytic conditions in Theorem 4.1.
Proof. Note that, if ![]() $l$ is odd, then
$l$ is odd, then 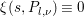 ${\it\xi}(s,P_{l,{\it\nu}})\equiv 0$, since
${\it\xi}(s,P_{l,{\it\nu}})\equiv 0$, since ![]() $A({\it\beta})$ is invariant under
$A({\it\beta})$ is invariant under 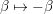 ${\it\beta}\mapsto -{\it\beta}$ and
${\it\beta}\mapsto -{\it\beta}$ and ![]() $P_{l,{\it\nu}}$ is homogeneous of degree
$P_{l,{\it\nu}}$ is homogeneous of degree ![]() $l$. For this we remark that, from Section 3,
$l$. For this we remark that, from Section 3, 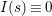 $I(s)\equiv 0$ also holds when
$I(s)\equiv 0$ also holds when ![]() $l$ is odd. From now on we assume that
$l$ is odd. From now on we assume that ![]() $l$ is even. Now suppose that the condition
$l$ is even. Now suppose that the condition 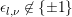 ${\it\epsilon}_{l,{\it\nu}}\not \in \{\pm 1\}$ is satisfied, which is equivalent to
${\it\epsilon}_{l,{\it\nu}}\not \in \{\pm 1\}$ is satisfied, which is equivalent to ![]() ${\it\epsilon}_{l,{\it\nu}}^{2}\not =1$. We see that
${\it\epsilon}_{l,{\it\nu}}^{2}\not =1$. We see that 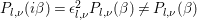 $P_{l,{\it\nu}}(i{\it\beta})={\it\epsilon}_{l,{\it\nu}}^{2}P_{l,{\it\nu}}({\it\beta})\not =P_{l,{\it\nu}}({\it\beta})$ for
$P_{l,{\it\nu}}(i{\it\beta})={\it\epsilon}_{l,{\it\nu}}^{2}P_{l,{\it\nu}}({\it\beta})\not =P_{l,{\it\nu}}({\it\beta})$ for ![]() ${\it\beta}\in \mathbb{H}$. In addition, we note that
${\it\beta}\in \mathbb{H}$. In addition, we note that 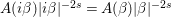 $A(i{\it\beta})|i{\it\beta}|^{-2s}=A({\it\beta})|{\it\beta}|^{-2s}$ for
$A(i{\it\beta})|i{\it\beta}|^{-2s}=A({\it\beta})|{\it\beta}|^{-2s}$ for ![]() ${\it\beta}\in S$. In the definition of
${\it\beta}\in S$. In the definition of 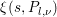 ${\it\xi}(s,P_{l,{\it\nu}})$, we can replace
${\it\xi}(s,P_{l,{\it\nu}})$, we can replace ![]() $S$ by
$S$ by ![]() $iS$. Hence, we obtain
$iS$. Hence, we obtain 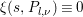 ${\it\xi}(s,P_{l,{\it\nu}})\equiv 0$, if
${\it\xi}(s,P_{l,{\it\nu}})\equiv 0$, if  ${\it\epsilon}_{l,{\it\nu}}\not \in \{\pm 1\}$.
${\it\epsilon}_{l,{\it\nu}}\not \in \{\pm 1\}$.
We now assume that  ${\it\epsilon}_{l,{\it\nu}}\in \{\pm 1\}$. By a formal calculation similar to [Reference Pitale22, Proposition 3.5] we get
${\it\epsilon}_{l,{\it\nu}}\in \{\pm 1\}$. By a formal calculation similar to [Reference Pitale22, Proposition 3.5] we get
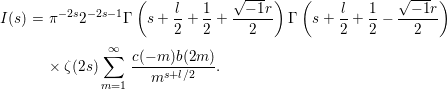 $$\begin{eqnarray}\displaystyle I(s) & = & \displaystyle {\it\pi}^{-2s}2^{-2s-1}{\rm\Gamma}\left(s+\frac{l}{2}+\frac{1}{2}+\frac{\sqrt{-1}r}{2}\right){\rm\Gamma}\left(s+\frac{l}{2}+\frac{1}{2}-\frac{\sqrt{-1}r}{2}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,{\it\zeta}(2s)\mathop{\sum }_{m=1}^{\infty }\frac{c(-m)b(2m)}{m^{s+l/2}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I(s) & = & \displaystyle {\it\pi}^{-2s}2^{-2s-1}{\rm\Gamma}\left(s+\frac{l}{2}+\frac{1}{2}+\frac{\sqrt{-1}r}{2}\right){\rm\Gamma}\left(s+\frac{l}{2}+\frac{1}{2}-\frac{\sqrt{-1}r}{2}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,{\it\zeta}(2s)\mathop{\sum }_{m=1}^{\infty }\frac{c(-m)b(2m)}{m^{s+l/2}}.\nonumber\end{eqnarray}$$ We put 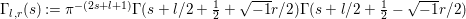 ${\rm\Gamma}_{l,r}(s):={\it\pi}^{-(2s+l+1)}{\rm\Gamma}(s+l/2+\frac{1}{2}+\sqrt{-1}r/2){\rm\Gamma}(s+l/2+\frac{1}{2}-\sqrt{-1}r/2)$. We have
${\rm\Gamma}_{l,r}(s):={\it\pi}^{-(2s+l+1)}{\rm\Gamma}(s+l/2+\frac{1}{2}+\sqrt{-1}r/2){\rm\Gamma}(s+l/2+\frac{1}{2}-\sqrt{-1}r/2)$. We have
 $$\begin{eqnarray}\displaystyle {\it\xi}(s+\frac{l}{2}+\frac{1}{2},P_{l,{\it\nu}}) & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}\frac{A({\it\beta})P_{l,{\it\nu}}({\it\beta})}{|{\it\beta}|^{2(s+l/2+1/2)}}\nonumber\\ \displaystyle & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}\frac{\displaystyle \mathop{\sum }_{t=0}^{u}\mathop{\sum }_{n|d}c(\frac{-|{\it\beta}|^{2}}{2^{t+1}n^{2}})(-{\it\epsilon})^{t}P_{l,{\it\nu}}({\it\beta})}{(|{\it\beta}|^{2})^{s+l/2}}\nonumber\\ \displaystyle & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}\mathop{\sum }_{t=0}^{u}\mathop{\sum }_{n|d}\frac{c(-\frac{|{\it\beta}|^{2}}{2^{t+1}n^{2}})(-{\it\epsilon})^{t}P_{l,{\it\nu}}(\frac{{\it\beta}}{2^{t/2}n})}{(2^{t}n^{2})^{s}(\frac{|{\it\beta}|^{2}}{2^{t}n^{2}})^{s+l/2}}\nonumber\\ \displaystyle & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{u=0}^{\infty }\mathop{\sum }_{\substack{ d\geqslant 1 \\ d:\text{odd}}}\mathop{\sum }_{{\it\beta}\in S^{\text{prim}}}\mathop{\sum }_{t=0}^{u}\mathop{\sum }_{n|d}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{c(-\frac{1}{2}|{\it\varpi}_{2}^{u-t}\frac{d}{n}{\it\beta}_{0}|^{2})(-{\it\epsilon}{\it\epsilon}_{l,{\it\nu}})^{t}P_{l,{\it\nu}}({\it\varpi}_{2}^{u-t}\frac{d}{n}{\it\beta}_{0})}{(2^{t}n^{2})^{s}|{\it\varpi}_{2}^{u-t}\frac{d}{n}{\it\beta}_{0}|^{2(s+l/2)}}\nonumber\\ \displaystyle & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{u=0}^{\infty }\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\substack{ d\geqslant 1 \\ d:\text{odd}}}\left(\mathop{\sum }_{t=0}^{u}\mathop{\sum }_{n|d}\mathop{\sum }_{{\it\beta}\in S^{\text{prim}}}\frac{c(-\frac{1}{2}|{\it\varpi}_{2}^{t}n{\it\beta}|^{2})P_{l,{\it\nu}}({\it\varpi}_{2}^{t}n{\it\beta})}{(-2^{s}{\it\epsilon}_{l,{\it\nu}}{\it\epsilon})^{u-t}(\frac{d}{n})^{2s}|{\it\varpi}_{2}^{t}n{\it\beta}|^{2(s+l/2)}}\right)\nonumber\\ \displaystyle & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{u=0}^{\infty }\frac{1}{(-2^{s}{\it\epsilon}_{l,{\it\nu}}{\it\epsilon})^{u}}\mathop{\sum }_{\substack{ d\geqslant 1 \\ d:\text{odd}}}\frac{1}{d^{2s}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{m=1}^{\infty }\frac{\displaystyle c(-m)\mathop{\sum }_{{\it\beta}\in S,|{\it\beta}|^{2}=2m}P_{l,{\it\nu}}({\it\beta})}{(2m)^{s+l/2}}\nonumber\\ \displaystyle & = & \displaystyle 2^{1-l/2}\frac{2^{2s}-1}{2^{s}+{\it\epsilon}_{l,{\it\nu}}{\it\epsilon}}2^{-2s-1}{\rm\Gamma}_{l,r}(s){\it\zeta}(2s)\mathop{\sum }_{m=1}^{\infty }\frac{c(-m)b(2m)}{m^{s+l/2}}\nonumber\\ \displaystyle & = & \displaystyle 2^{1-l/2}{\it\pi}^{-(l+1)}(2^{s}-{\it\epsilon}_{l,{\it\nu}}{\it\epsilon})I(s).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\xi}(s+\frac{l}{2}+\frac{1}{2},P_{l,{\it\nu}}) & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}\frac{A({\it\beta})P_{l,{\it\nu}}({\it\beta})}{|{\it\beta}|^{2(s+l/2+1/2)}}\nonumber\\ \displaystyle & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}\frac{\displaystyle \mathop{\sum }_{t=0}^{u}\mathop{\sum }_{n|d}c(\frac{-|{\it\beta}|^{2}}{2^{t+1}n^{2}})(-{\it\epsilon})^{t}P_{l,{\it\nu}}({\it\beta})}{(|{\it\beta}|^{2})^{s+l/2}}\nonumber\\ \displaystyle & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}\mathop{\sum }_{t=0}^{u}\mathop{\sum }_{n|d}\frac{c(-\frac{|{\it\beta}|^{2}}{2^{t+1}n^{2}})(-{\it\epsilon})^{t}P_{l,{\it\nu}}(\frac{{\it\beta}}{2^{t/2}n})}{(2^{t}n^{2})^{s}(\frac{|{\it\beta}|^{2}}{2^{t}n^{2}})^{s+l/2}}\nonumber\\ \displaystyle & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{u=0}^{\infty }\mathop{\sum }_{\substack{ d\geqslant 1 \\ d:\text{odd}}}\mathop{\sum }_{{\it\beta}\in S^{\text{prim}}}\mathop{\sum }_{t=0}^{u}\mathop{\sum }_{n|d}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{c(-\frac{1}{2}|{\it\varpi}_{2}^{u-t}\frac{d}{n}{\it\beta}_{0}|^{2})(-{\it\epsilon}{\it\epsilon}_{l,{\it\nu}})^{t}P_{l,{\it\nu}}({\it\varpi}_{2}^{u-t}\frac{d}{n}{\it\beta}_{0})}{(2^{t}n^{2})^{s}|{\it\varpi}_{2}^{u-t}\frac{d}{n}{\it\beta}_{0}|^{2(s+l/2)}}\nonumber\\ \displaystyle & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{u=0}^{\infty }\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\substack{ d\geqslant 1 \\ d:\text{odd}}}\left(\mathop{\sum }_{t=0}^{u}\mathop{\sum }_{n|d}\mathop{\sum }_{{\it\beta}\in S^{\text{prim}}}\frac{c(-\frac{1}{2}|{\it\varpi}_{2}^{t}n{\it\beta}|^{2})P_{l,{\it\nu}}({\it\varpi}_{2}^{t}n{\it\beta})}{(-2^{s}{\it\epsilon}_{l,{\it\nu}}{\it\epsilon})^{u-t}(\frac{d}{n})^{2s}|{\it\varpi}_{2}^{t}n{\it\beta}|^{2(s+l/2)}}\right)\nonumber\\ \displaystyle & = & \displaystyle {\rm\Gamma}_{l,r}(s)\mathop{\sum }_{u=0}^{\infty }\frac{1}{(-2^{s}{\it\epsilon}_{l,{\it\nu}}{\it\epsilon})^{u}}\mathop{\sum }_{\substack{ d\geqslant 1 \\ d:\text{odd}}}\frac{1}{d^{2s}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{m=1}^{\infty }\frac{\displaystyle c(-m)\mathop{\sum }_{{\it\beta}\in S,|{\it\beta}|^{2}=2m}P_{l,{\it\nu}}({\it\beta})}{(2m)^{s+l/2}}\nonumber\\ \displaystyle & = & \displaystyle 2^{1-l/2}\frac{2^{2s}-1}{2^{s}+{\it\epsilon}_{l,{\it\nu}}{\it\epsilon}}2^{-2s-1}{\rm\Gamma}_{l,r}(s){\it\zeta}(2s)\mathop{\sum }_{m=1}^{\infty }\frac{c(-m)b(2m)}{m^{s+l/2}}\nonumber\\ \displaystyle & = & \displaystyle 2^{1-l/2}{\it\pi}^{-(l+1)}(2^{s}-{\it\epsilon}_{l,{\it\nu}}{\it\epsilon})I(s).\nonumber\end{eqnarray}$$ We note that 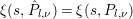 ${\it\xi}(s,\hat{P}_{l,{\it\nu}})={\it\xi}(s,P_{l,{\it\nu}})$ since
${\it\xi}(s,\hat{P}_{l,{\it\nu}})={\it\xi}(s,P_{l,{\it\nu}})$ since ![]() $S=\bar{S}$. The formula just proved and Theorem 3.3 then imply that
$S=\bar{S}$. The formula just proved and Theorem 3.3 then imply that 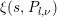 ${\it\xi}(s,P_{l,{\it\nu}})$ satisfies the desired three analytic properties in Theorem 4.1.◻
${\it\xi}(s,P_{l,{\it\nu}})$ satisfies the desired three analytic properties in Theorem 4.1.◻
Remark 4.3. Note that the definition (4.2) of ![]() $A({\it\beta})$ is very similar to the formula for the Fourier coefficient of the lift in the Saito–Kurokawa case (see [Reference Duke and Imamoḡlu7, page 348]) and the
$A({\it\beta})$ is very similar to the formula for the Fourier coefficient of the lift in the Saito–Kurokawa case (see [Reference Duke and Imamoḡlu7, page 348]) and the 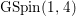 $\text{GSpin}(1,4)$ case [Reference Pitale22, (3.4)].
$\text{GSpin}(1,4)$ case [Reference Pitale22, (3.4)].
Theorem 4.4. Let 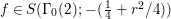 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ with Fourier coefficients
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ with Fourier coefficients ![]() $c(n)$ and with eigenvalue
$c(n)$ and with eigenvalue ![]() ${\it\epsilon}$ of the Atkin–Lehner involution. Define
${\it\epsilon}$ of the Atkin–Lehner involution. Define
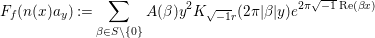 $$\begin{eqnarray}F_{f}(n(x)a_{y}):=\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}A({\it\beta})y^{2}K_{\sqrt{-1}r}(2{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{Re}({\it\beta}x)}\end{eqnarray}$$
$$\begin{eqnarray}F_{f}(n(x)a_{y}):=\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}A({\it\beta})y^{2}K_{\sqrt{-1}r}(2{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{Re}({\it\beta}x)}\end{eqnarray}$$ with 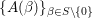 $\{A({\it\beta})\}_{{\it\beta}\in S\setminus \{0\}}$ defined by (4.2). Then we have
$\{A({\it\beta})\}_{{\it\beta}\in S\setminus \{0\}}$ defined by (4.2). Then we have  $F_{f}\in {\mathcal{M}}(\text{GL}_{2}({\mathcal{O}});r)$ and
$F_{f}\in {\mathcal{M}}(\text{GL}_{2}({\mathcal{O}});r)$ and ![]() $F_{f}$ is a cusp form. Furthermore,
$F_{f}$ is a cusp form. Furthermore, ![]() $F_{f}\not \equiv 0$ if
$F_{f}\not \equiv 0$ if ![]() $f\not \equiv 0$.
$f\not \equiv 0$.
Proof. We can verify the left invariance of ![]() $F_{f}$ with respect to
$F_{f}$ with respect to 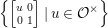 $\left\{\left[\!\begin{smallmatrix}u & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]\mid u\in {\mathcal{O}}^{\times }\right\}$ in a straightforward way. Proposition 2.2, Theorem 4.1 and Proposition 4.2 thus imply
$\left\{\left[\!\begin{smallmatrix}u & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]\mid u\in {\mathcal{O}}^{\times }\right\}$ in a straightforward way. Proposition 2.2, Theorem 4.1 and Proposition 4.2 thus imply 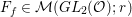 $F_{f}\in {\mathcal{M}}(GL_{2}({\mathcal{O}});r)$. Since
$F_{f}\in {\mathcal{M}}(GL_{2}({\mathcal{O}});r)$. Since  $\text{GL}_{2}({\mathcal{O}})$ has only one cusp (see Lemma 2.3), the Fourier expansion of
$\text{GL}_{2}({\mathcal{O}})$ has only one cusp (see Lemma 2.3), the Fourier expansion of ![]() $F_{f}$ means that
$F_{f}$ means that ![]() $F_{f}$ is cuspidal. To show the nonvanishing we need the following lemma.
$F_{f}$ is cuspidal. To show the nonvanishing we need the following lemma.
Lemma 4.5. Let 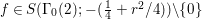 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))\setminus \{0\}$ with Fourier coefficients
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))\setminus \{0\}$ with Fourier coefficients ![]() $c(n)$ and with eigenvalue
$c(n)$ and with eigenvalue ![]() ${\it\epsilon}$ of the Atkin–Lehner involution. Then, there exist
${\it\epsilon}$ of the Atkin–Lehner involution. Then, there exist 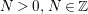 $N>0,N\in \mathbb{Z}$, such that
$N>0,N\in \mathbb{Z}$, such that 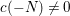 $c(-N)\neq 0$.
$c(-N)\neq 0$.
Proof. Assume that 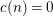 $c(n)=0$ for all
$c(n)=0$ for all ![]() $n<0$. Set
$n<0$. Set 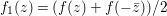 $f_{1}(z)=(f(z)+f(-\bar{z}))/2$ and
$f_{1}(z)=(f(z)+f(-\bar{z}))/2$ and 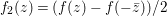 $f_{2}(z)=(f(z)-f(-\bar{z}))/2$. Then,
$f_{2}(z)=(f(z)-f(-\bar{z}))/2$. Then, ![]() $f_{1},f_{2}$ are elements of
$f_{1},f_{2}$ are elements of 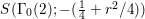 $S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ with the same eigenvalue
$S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ with the same eigenvalue ![]() ${\it\epsilon}$ of the Atkin–Lehner involution as
${\it\epsilon}$ of the Atkin–Lehner involution as ![]() $f$. In addition,
$f$. In addition, ![]() $f_{1}$ is an even Maass form and
$f_{1}$ is an even Maass form and ![]() $f_{2}$ is an odd Maass form, with the property that they have the exact same Fourier coefficients corresponding to positive indices. This implies that the
$f_{2}$ is an odd Maass form, with the property that they have the exact same Fourier coefficients corresponding to positive indices. This implies that the ![]() $L$-functions for
$L$-functions for ![]() $f_{1}$ and
$f_{1}$ and ![]() $f_{2}$ satisfy
$f_{2}$ satisfy 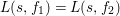 $L(s,f_{1})=L(s,f_{2})$. On the other hand,
$L(s,f_{1})=L(s,f_{2})$. On the other hand, 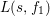 $L(s,f_{1})$ and
$L(s,f_{1})$ and 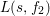 $L(s,f_{2})$ satisfy functional equations with the gamma factors shifted by
$L(s,f_{2})$ satisfy functional equations with the gamma factors shifted by ![]() $1$. Here, we use that both
$1$. Here, we use that both ![]() $f_{1}$ and
$f_{1}$ and ![]() $f_{2}$ have the same Atkin–Lehner eigenvalue. If
$f_{2}$ have the same Atkin–Lehner eigenvalue. If 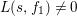 $L(s,f_{1})\neq 0$, we obtain an identity of gamma factors, which can be checked to be impossible. This gives us that
$L(s,f_{1})\neq 0$, we obtain an identity of gamma factors, which can be checked to be impossible. This gives us that ![]() $f$ has to be zero, a contradiction.◻
$f$ has to be zero, a contradiction.◻
Let ![]() $N_{0}$ be the smallest positive integer such that
$N_{0}$ be the smallest positive integer such that 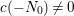 $c(-N_{0})\neq 0$. Let
$c(-N_{0})\neq 0$. Let ![]() ${\it\beta}_{0}\in {\mathcal{O}}$ be such that
${\it\beta}_{0}\in {\mathcal{O}}$ be such that 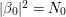 $|{\it\beta}_{0}|^{2}=N_{0}$. Choose
$|{\it\beta}_{0}|^{2}=N_{0}$. Choose 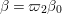 ${\it\beta}={\it\varpi}_{2}{\it\beta}_{0}$. Then, by the choice of
${\it\beta}={\it\varpi}_{2}{\it\beta}_{0}$. Then, by the choice of ![]() $N_{0}$ and the definition of
$N_{0}$ and the definition of ![]() $A({\it\beta})$, we see that
$A({\it\beta})$, we see that 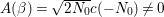 $A({\it\beta})=\sqrt{2N_{0}}c(-N_{0})\neq 0$, as required.◻
$A({\it\beta})=\sqrt{2N_{0}}c(-N_{0})\neq 0$, as required.◻
Remark 4.6. Weyl’s law for congruence subgroups of ![]() $\text{SL}_{2}(\mathbb{Z})$ by Selberg (cf. [Reference Iwaniec12, §11.1]) implies that there exist Maass cusp forms for
$\text{SL}_{2}(\mathbb{Z})$ by Selberg (cf. [Reference Iwaniec12, §11.1]) implies that there exist Maass cusp forms for ![]() ${\rm\Gamma}_{0}(2)$. This and the theorem above imply the existence of nonzero lifts
${\rm\Gamma}_{0}(2)$. This and the theorem above imply the existence of nonzero lifts ![]() $F_{f}$.
$F_{f}$.
5 Actions of Hecke operators on the lifting
5.1 Adelization of automorphic forms
To study the actions of Hecke operators on our cusp forms constructed by the lifting we need both adelic and nonadelic treatments of automorphic forms.
For a complex number ![]() $r\in \mathbb{C}$ we introduce another space
$r\in \mathbb{C}$ we introduce another space  $M({\mathcal{G}}(\mathbb{A}),r)$ of automorphic forms for
$M({\mathcal{G}}(\mathbb{A}),r)$ of automorphic forms for ![]() ${\mathcal{G}}$.
${\mathcal{G}}$.
Definition 5.1. Let  $M({\mathcal{G}}(\mathbb{A}),r)$ be the space of smooth functions
$M({\mathcal{G}}(\mathbb{A}),r)$ be the space of smooth functions ![]() ${\rm\Phi}$ on
${\rm\Phi}$ on ![]() ${\mathcal{G}}(\mathbb{A})$ satisfying the following conditions:
${\mathcal{G}}(\mathbb{A})$ satisfying the following conditions:
(1)
 ${\rm\Phi}(z{\it\gamma}gu_{f}u_{\infty })={\rm\Phi}(g)$ for any
${\rm\Phi}(z{\it\gamma}gu_{f}u_{\infty })={\rm\Phi}(g)$ for any  $(z,{\it\gamma},g,u_{f},u_{\infty })\in Z_{\mathbb{A}}\times {\mathcal{G}}(\mathbb{Q})\times {\mathcal{G}}(\mathbb{A})\times U\times K$, where
$(z,{\it\gamma},g,u_{f},u_{\infty })\in Z_{\mathbb{A}}\times {\mathcal{G}}(\mathbb{Q})\times {\mathcal{G}}(\mathbb{A})\times U\times K$, where  $Z_{\mathbb{A}}$ denotes the center of
$Z_{\mathbb{A}}$ denotes the center of  ${\mathcal{G}}(\mathbb{A})$;
${\mathcal{G}}(\mathbb{A})$;(2)
 ${\rm\Omega}\cdot {\rm\Phi}(g_{\infty })=-\frac{1}{2}(r^{2}/4+1){\rm\Phi}(g_{\infty })$ for any
${\rm\Omega}\cdot {\rm\Phi}(g_{\infty })=-\frac{1}{2}(r^{2}/4+1){\rm\Phi}(g_{\infty })$ for any  $g_{\infty }\in {\mathcal{G}}(\mathbb{R})=\text{GL}_{2}(\mathbb{H})$;
$g_{\infty }\in {\mathcal{G}}(\mathbb{R})=\text{GL}_{2}(\mathbb{H})$;(3)
 ${\rm\Phi}$ is of moderate growth.
${\rm\Phi}$ is of moderate growth.
According to part (1) of Lemma 2.3, the class number of ![]() ${\mathcal{G}}$ with respect to
${\mathcal{G}}$ with respect to ![]() $U$ is one, which means that
$U$ is one, which means that 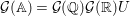 ${\mathcal{G}}(\mathbb{A})={\mathcal{G}}(\mathbb{Q}){\mathcal{G}}(\mathbb{R})U$. We can thus view
${\mathcal{G}}(\mathbb{A})={\mathcal{G}}(\mathbb{Q}){\mathcal{G}}(\mathbb{R})U$. We can thus view  $F\in M(\text{GL}_{2}({\mathcal{O}}),r)$ as a smooth function
$F\in M(\text{GL}_{2}({\mathcal{O}}),r)$ as a smooth function ![]() ${\rm\Phi}_{F}$ on
${\rm\Phi}_{F}$ on ![]() ${\mathcal{G}}(\mathbb{A})$ by
${\mathcal{G}}(\mathbb{A})$ by
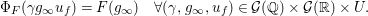 $$\begin{eqnarray}{\rm\Phi}_{F}({\it\gamma}g_{\infty }u_{f})=F(g_{\infty })\quad \forall ({\it\gamma},g_{\infty },u_{f})\in {\mathcal{G}}(\mathbb{Q})\times {\mathcal{G}}(\mathbb{R})\times U.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Phi}_{F}({\it\gamma}g_{\infty }u_{f})=F(g_{\infty })\quad \forall ({\it\gamma},g_{\infty },u_{f})\in {\mathcal{G}}(\mathbb{Q})\times {\mathcal{G}}(\mathbb{R})\times U.\end{eqnarray}$$We therefore see the following.
Lemma 5.2. We have an isomorphism 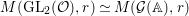 $M(\text{GL}_{2}({\mathcal{O}}),r)\simeq M({\mathcal{G}}(\mathbb{A}),r)$.
$M(\text{GL}_{2}({\mathcal{O}}),r)\simeq M({\mathcal{G}}(\mathbb{A}),r)$.
5.2 Hecke operators
For each place ![]() $p\leqslant \infty$, let
$p\leqslant \infty$, let 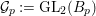 ${\mathcal{G}}_{p}:=\text{GL}_{2}(B_{p})$, with
${\mathcal{G}}_{p}:=\text{GL}_{2}(B_{p})$, with 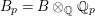 $B_{p}=B\otimes _{\mathbb{Q}}\mathbb{Q}_{p}$. For a finite prime
$B_{p}=B\otimes _{\mathbb{Q}}\mathbb{Q}_{p}$. For a finite prime ![]() $p\not =2$, we have
$p\not =2$, we have 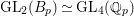 $\text{GL}_{2}(B_{p})\simeq \text{GL}_{4}(\mathbb{Q}_{p})$. Let
$\text{GL}_{2}(B_{p})\simeq \text{GL}_{4}(\mathbb{Q}_{p})$. Let ![]() ${\mathcal{O}}_{p}$ be the
${\mathcal{O}}_{p}$ be the ![]() $p$-adic completion of
$p$-adic completion of ![]() ${\mathcal{O}}$ for
${\mathcal{O}}$ for ![]() $p<\infty$. For a finite prime
$p<\infty$. For a finite prime ![]() $p\not =2$,
$p\not =2$, 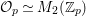 ${\mathcal{O}}_{p}\simeq M_{2}(\mathbb{Z}_{p})$ and
${\mathcal{O}}_{p}\simeq M_{2}(\mathbb{Z}_{p})$ and 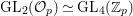 $\text{GL}_{2}({\mathcal{O}}_{p})\simeq \text{GL}_{4}(\mathbb{Z}_{p})$. Set
$\text{GL}_{2}({\mathcal{O}}_{p})\simeq \text{GL}_{4}(\mathbb{Z}_{p})$. Set 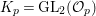 $K_{p}=\text{GL}_{2}({\mathcal{O}}_{p})$ for
$K_{p}=\text{GL}_{2}({\mathcal{O}}_{p})$ for ![]() $p<\infty$.
$p<\infty$.
We denote by 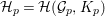 ${\mathcal{H}}_{p}={\mathcal{H}}({\mathcal{G}}_{p},K_{p})$ the Hecke algebra for
${\mathcal{H}}_{p}={\mathcal{H}}({\mathcal{G}}_{p},K_{p})$ the Hecke algebra for 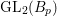 $\text{GL}_{2}(B_{p})$ with respect to
$\text{GL}_{2}(B_{p})$ with respect to 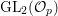 $\text{GL}_{2}({\mathcal{O}}_{p})$ for
$\text{GL}_{2}({\mathcal{O}}_{p})$ for ![]() $p<\infty$. According to [Reference Satake26, §8, Theorem 6],
$p<\infty$. According to [Reference Satake26, §8, Theorem 6], ![]() ${\mathcal{H}}_{p}$ has the following generators:
${\mathcal{H}}_{p}$ has the following generators:
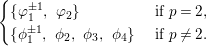 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\{{\it\varphi}_{1}^{\pm 1},~{\it\varphi}_{2}\}\quad & \text{if }p=2,\\ \{{\it\phi}_{1}^{\pm 1},~{\it\phi}_{2},~{\it\phi}_{3},~{\it\phi}_{4}\}\quad & \text{if }p\not =2.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\{{\it\varphi}_{1}^{\pm 1},~{\it\varphi}_{2}\}\quad & \text{if }p=2,\\ \{{\it\phi}_{1}^{\pm 1},~{\it\phi}_{2},~{\it\phi}_{3},~{\it\phi}_{4}\}\quad & \text{if }p\not =2.\end{array}\right.\end{eqnarray}$$ Here, ![]() ${\it\varphi}_{1},~{\it\varphi}_{2}$ denote the characteristic functions for
${\it\varphi}_{1},~{\it\varphi}_{2}$ denote the characteristic functions for
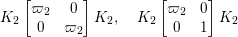 $$\begin{eqnarray}K_{2}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & 0\\ 0 & {\it\varpi}_{2}\end{array}\right]K_{2},\quad K_{2}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & 0\\ 0 & 1\end{array}\right]K_{2}\end{eqnarray}$$
$$\begin{eqnarray}K_{2}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & 0\\ 0 & {\it\varpi}_{2}\end{array}\right]K_{2},\quad K_{2}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & 0\\ 0 & 1\end{array}\right]K_{2}\end{eqnarray}$$ respectively, and  ${\it\phi}_{1},~{\it\phi}_{2},~{\it\phi}_{3},~{\it\phi}_{4}$ denote the characteristic functions for
${\it\phi}_{1},~{\it\phi}_{2},~{\it\phi}_{3},~{\it\phi}_{4}$ denote the characteristic functions for
 $$\begin{eqnarray}\displaystyle K_{p}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & p & \\ & & & p\end{array}\right]K_{p},~K_{p}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & p & \\ & & & 1\end{array}\right]K_{p}, & & \displaystyle \nonumber\\ \displaystyle ~K_{p}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p},~K_{p}\left[\begin{array}{@{}cccc@{}}p & & & \\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{p}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & p & \\ & & & p\end{array}\right]K_{p},~K_{p}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & p & \\ & & & 1\end{array}\right]K_{p}, & & \displaystyle \nonumber\\ \displaystyle ~K_{p}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p},~K_{p}\left[\begin{array}{@{}cccc@{}}p & & & \\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p} & & \displaystyle\end{eqnarray}$$ respectively when ![]() $p\not =2$. Recall that
$p\not =2$. Recall that ![]() ${\it\varpi}_{2}$ denotes a prime element of
${\it\varpi}_{2}$ denotes a prime element of ![]() $B_{2}$. We want to obtain the single coset decomposition for the above double cosets. For that, we next review the Bruhat decomposition of
$B_{2}$. We want to obtain the single coset decomposition for the above double cosets. For that, we next review the Bruhat decomposition of ![]() $K_{p}$ given by
$K_{p}$ given by
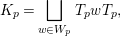 $$\begin{eqnarray}K_{p}=\mathop{\sqcup }_{w\in W_{p}}T_{p}wT_{p},\end{eqnarray}$$
$$\begin{eqnarray}K_{p}=\mathop{\sqcup }_{w\in W_{p}}T_{p}wT_{p},\end{eqnarray}$$ where ![]() $W_{p}$ denotes the Weyl group of
$W_{p}$ denotes the Weyl group of 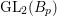 $\text{GL}_{2}(B_{p})$, and
$\text{GL}_{2}(B_{p})$, and ![]() $T_{p}$ is the subgroup of elements in
$T_{p}$ is the subgroup of elements in ![]() $K_{p}$ which are upper triangular modulo
$K_{p}$ which are upper triangular modulo ![]() $p$ for an odd
$p$ for an odd ![]() $p$ (respectively, upper triangular modulo
$p$ (respectively, upper triangular modulo ![]() ${\it\varpi}_{2}{\mathcal{O}}_{2}$ for
${\it\varpi}_{2}{\mathcal{O}}_{2}$ for ![]() $p=2$).
$p=2$).
Let ![]() $N_{p}$ be the standard maximal unipotent subgroup of
$N_{p}$ be the standard maximal unipotent subgroup of 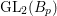 $\text{GL}_{2}(B_{p})$ defined over
$\text{GL}_{2}(B_{p})$ defined over ![]() $\mathbb{Q}_{p}$. We put
$\mathbb{Q}_{p}$. We put 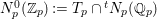 $N_{p}^{0}(\mathbb{Z}_{p}):=T_{p}\cap \text{}^{t}N_{p}(\mathbb{Q}_{p})$. We furthermore introduce
$N_{p}^{0}(\mathbb{Z}_{p}):=T_{p}\cap \text{}^{t}N_{p}(\mathbb{Q}_{p})$. We furthermore introduce 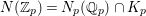 $N(\mathbb{Z}_{p})=N_{p}(\mathbb{Q}_{p})\cap K_{p}$ and
$N(\mathbb{Z}_{p})=N_{p}(\mathbb{Q}_{p})\cap K_{p}$ and 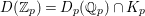 $D(\mathbb{Z}_{p})=D_{p}(\mathbb{Q}_{p})\cap K_{p}$, where
$D(\mathbb{Z}_{p})=D_{p}(\mathbb{Q}_{p})\cap K_{p}$, where ![]() $D_{p}$ denotes the subgroup of diagonal matrices in
$D_{p}$ denotes the subgroup of diagonal matrices in 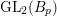 $\text{GL}_{2}(B_{p})$. Then we have the Iwahori decomposition
$\text{GL}_{2}(B_{p})$. Then we have the Iwahori decomposition
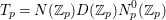 $$\begin{eqnarray}T_{p}=N(\mathbb{Z}_{p})D(\mathbb{Z}_{p})N_{p}^{0}(\mathbb{Z}_{p})\end{eqnarray}$$
$$\begin{eqnarray}T_{p}=N(\mathbb{Z}_{p})D(\mathbb{Z}_{p})N_{p}^{0}(\mathbb{Z}_{p})\end{eqnarray}$$ (see [Reference Iwahori and Matsumoto13, Theorem 2.5]). Let ![]() $h$ be one of
$h$ be one of
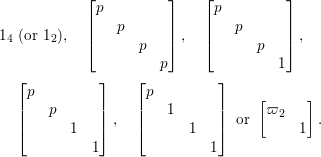 $$\begin{eqnarray}\displaystyle 1_{4}~(\text{or }1_{2}),\quad \left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & p & \\ & & & p\end{array}\right],\quad \left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & p & \\ & & & 1\end{array}\right],\quad & & \displaystyle \nonumber\\ \displaystyle \left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & 1 & \\ & & & 1\end{array}\right],\quad \left[\begin{array}{@{}cccc@{}}p & & & \\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]~\text{or}~\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & \\ & 1\end{array}\right]. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1_{4}~(\text{or }1_{2}),\quad \left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & p & \\ & & & p\end{array}\right],\quad \left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & p & \\ & & & 1\end{array}\right],\quad & & \displaystyle \nonumber\\ \displaystyle \left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & 1 & \\ & & & 1\end{array}\right],\quad \left[\begin{array}{@{}cccc@{}}p & & & \\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]~\text{or}~\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & \\ & 1\end{array}\right]. & & \displaystyle \nonumber\end{eqnarray}$$ $$\begin{eqnarray}K_{p}hK_{p}=\mathop{\sqcup }_{w\in W_{p}/W_{p}(h)}N(\mathbb{Z}_{p})whK_{p},\end{eqnarray}$$
$$\begin{eqnarray}K_{p}hK_{p}=\mathop{\sqcup }_{w\in W_{p}/W_{p}(h)}N(\mathbb{Z}_{p})whK_{p},\end{eqnarray}$$ where  $W_{p}(h):=\{w\in W_{p}\mid whw^{-1}=h\}$.
$W_{p}(h):=\{w\in W_{p}\mid whw^{-1}=h\}$.
To describe this coset decomposition of ![]() $K_{p}hK_{p}$ explicitly, we need a set of representatives for
$K_{p}hK_{p}$ explicitly, we need a set of representatives for  $W_{p}/W_{p}(h)$.
$W_{p}/W_{p}(h)$.
(1) Let
 $p=2$. For
$p=2$. For  $h=\left[\!\begin{smallmatrix}{\it\varpi}_{2} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]$ we can take as a set of representatives for
$h=\left[\!\begin{smallmatrix}{\it\varpi}_{2} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]$ we can take as a set of representatives for $$\begin{eqnarray}\left\{1_{2},~\left[\begin{array}{@{}cc@{}}0 & 1\\ 1 & 0\end{array}\right]\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left\{1_{2},~\left[\begin{array}{@{}cc@{}}0 & 1\\ 1 & 0\end{array}\right]\right\}\end{eqnarray}$$ $W_{2}/W_{2}(h)$.
$W_{2}/W_{2}(h)$.(2) Let
 $p\not =2$.
$p\not =2$.(a) When
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & p & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we can take as a set of representatives for
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & p & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we can take as a set of representatives for $$\begin{eqnarray}\left\{1_{4},~\left[\begin{array}{@{}cccc@{}}0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0\end{array}\right],~\left[\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\end{array}\right],~\left[\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\end{array}\right]\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left\{1_{4},~\left[\begin{array}{@{}cccc@{}}0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0\end{array}\right],~\left[\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\end{array}\right],~\left[\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\end{array}\right]\right\}\end{eqnarray}$$ $W_{p}/W_{p}(h)$.
$W_{p}/W_{p}(h)$.(b) When
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & 1 & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we can take as a set of representatives for
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & 1 & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we can take as a set of representatives for $$\begin{eqnarray}\left\{1_{4},~\left[\begin{array}{@{}cccc@{}}0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0\end{array}\right],~\left[\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\end{array}\right],~\left[\begin{array}{@{}cccc@{}}0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right]\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left\{1_{4},~\left[\begin{array}{@{}cccc@{}}0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0\end{array}\right],~\left[\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\end{array}\right],~\left[\begin{array}{@{}cccc@{}}0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right]\right\}\end{eqnarray}$$ $W_{p}/W_{p}(h)$.
$W_{p}/W_{p}(h)$.(c) When
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we can take as a set of representatives for
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we can take as a set of representatives for $$\begin{eqnarray}\displaystyle & \left\{1_{4},~\left[\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\end{array}\right],~\left[\begin{array}{@{}cccc@{}}0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0\end{array}\right],~\left[\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\end{array}\right],\right. & \displaystyle \nonumber\\ \displaystyle & \quad \quad \left.\left[\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\end{array}\right],\left[\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\end{array}\right]\right\} & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \left\{1_{4},~\left[\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\end{array}\right],~\left[\begin{array}{@{}cccc@{}}0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0\end{array}\right],~\left[\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\end{array}\right],\right. & \displaystyle \nonumber\\ \displaystyle & \quad \quad \left.\left[\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\end{array}\right],\left[\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\end{array}\right]\right\} & \displaystyle \nonumber\end{eqnarray}$$ $W_{p}/W_{p}(h)$.
$W_{p}/W_{p}(h)$.
By Lemmas 5.3 and 5.4, we are now able to write down the coset decomposition of ![]() $K_{p}hK_{p}$ explicitly.
$K_{p}hK_{p}$ explicitly.
(1) Let
 $p=2$ and
$p=2$ and  $h=\left[\!\begin{smallmatrix}{\it\varpi}_{2} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]$. We have
$h=\left[\!\begin{smallmatrix}{\it\varpi}_{2} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]$. We have  $$\begin{eqnarray}K_{2}hK_{2}=\left[\begin{array}{@{}cc@{}}1 & 0\\ 0 & {\it\varpi}_{2}\end{array}\right]K_{2}\sqcup \mathop{\sqcup }_{x\in {\mathcal{O}}_{2}/{\it\varpi}_{2}{\mathcal{O}}_{2}}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & 0\\ 0 & 1\end{array}\right]\left[\begin{array}{@{}cc@{}}1 & {\it\varpi}_{2}^{-1}x\\ 0 & 1\end{array}\right]K_{2}.\end{eqnarray}$$
$$\begin{eqnarray}K_{2}hK_{2}=\left[\begin{array}{@{}cc@{}}1 & 0\\ 0 & {\it\varpi}_{2}\end{array}\right]K_{2}\sqcup \mathop{\sqcup }_{x\in {\mathcal{O}}_{2}/{\it\varpi}_{2}{\mathcal{O}}_{2}}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & 0\\ 0 & 1\end{array}\right]\left[\begin{array}{@{}cc@{}}1 & {\it\varpi}_{2}^{-1}x\\ 0 & 1\end{array}\right]K_{2}.\end{eqnarray}$$(2) Let
 $p\not =2$.
$p\not =2$.(a) For
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & p & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we have
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & p & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we have  $$\begin{eqnarray}\displaystyle K_{p}hK_{p} & = & \displaystyle \mathop{\sqcup }_{x_{14},x_{24},x_{34}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & p & x_{34}\\ & & & 1\end{array}\right]\!\left[\begin{array}{@{}cccc@{}}1 & & & p^{-1}x_{14}\\ & 1 & & p^{-1}x_{24}\\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{12}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & x_{12} & & \\ & 1 & & \\ & & p & \\ & & & p\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{13},x_{23}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & 1 & \\ & & & p\end{array}\right]\left[\begin{array}{@{}cccc@{}}1 & & p^{-1}x_{13} & \\ & 1 & p^{-1}x_{23} & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \left[\begin{array}{@{}cccc@{}}1 & & & \\ & p & & \\ & & p & \\ & & & p\end{array}\right]K_{p}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{p}hK_{p} & = & \displaystyle \mathop{\sqcup }_{x_{14},x_{24},x_{34}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & p & x_{34}\\ & & & 1\end{array}\right]\!\left[\begin{array}{@{}cccc@{}}1 & & & p^{-1}x_{14}\\ & 1 & & p^{-1}x_{24}\\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{12}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & x_{12} & & \\ & 1 & & \\ & & p & \\ & & & p\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{13},x_{23}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & 1 & \\ & & & p\end{array}\right]\left[\begin{array}{@{}cccc@{}}1 & & p^{-1}x_{13} & \\ & 1 & p^{-1}x_{23} & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \left[\begin{array}{@{}cccc@{}}1 & & & \\ & p & & \\ & & p & \\ & & & p\end{array}\right]K_{p}.\nonumber\end{eqnarray}$$(b) For
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & 1 & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we have
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & 1 & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we have  $$\begin{eqnarray}\displaystyle K_{p}hK_{p} & = & \displaystyle \mathop{\sqcup }_{x_{12},x_{13},x_{14}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & x_{12} & & \\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\begin{array}{@{}cccc@{}}1 & & p^{-1}x_{13} & p^{-1}x_{14}\\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{34}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & & \\ & & p & x_{34}\\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{23},x_{24}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}1 & & & \\ & p & & \\ & & 1 & \\ & & & 1\end{array}\right]\!\!\left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & p^{-1}x_{23} & p^{-1}x_{24}\\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & & \\ & & 1 & \\ & & & p\end{array}\right]K_{p}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{p}hK_{p} & = & \displaystyle \mathop{\sqcup }_{x_{12},x_{13},x_{14}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & x_{12} & & \\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\begin{array}{@{}cccc@{}}1 & & p^{-1}x_{13} & p^{-1}x_{14}\\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{34}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & & \\ & & p & x_{34}\\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{23},x_{24}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}1 & & & \\ & p & & \\ & & 1 & \\ & & & 1\end{array}\right]\!\!\left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & p^{-1}x_{23} & p^{-1}x_{24}\\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & & \\ & & 1 & \\ & & & p\end{array}\right]K_{p}.\nonumber\end{eqnarray}$$(c) For
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we have
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$ we have  $$\begin{eqnarray}\displaystyle K_{p}hK_{p} & = & \displaystyle \mathop{\sqcup }_{x_{13},x_{14},x_{23},x_{24}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & 1 & \\ & & & 1\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\begin{array}{@{}cccc@{}}1 & & p^{-1}x_{13} & p^{-1}x_{14}\\ & 1 & p^{-1}x_{23} & p^{-1}x_{24}\\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{24},x_{34}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}1 & & & \\ & p & & \\ & & p & x_{34}\\ & & & 1\end{array}\right]\left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & & p^{-1}x_{24}\\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{23}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}1 & & & \\ & p & & \\ & & 1 & \\ & & & p\end{array}\right]\left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & p^{-1}x_{23} & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{12},x_{14},x_{34}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\!\!\left[\begin{array}{@{}cccc@{}}p & x_{12} & & \\ & 1 & & \\ & & p & x_{34}\\ & & & 1\end{array}\right]\!\!\left[\begin{array}{@{}cccc@{}}1 & & & p^{-1}x_{14}\\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]\!K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{12},x_{13}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & x_{12} & & \\ & 1 & & \\ & & 1 & \\ & & & p\end{array}\right]\left[\begin{array}{@{}cccc@{}}1 & & p^{-1}x_{13} & \\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & & \\ & & p & \\ & & & p\end{array}\right]K_{p}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{p}hK_{p} & = & \displaystyle \mathop{\sqcup }_{x_{13},x_{14},x_{23},x_{24}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & & & \\ & p & & \\ & & 1 & \\ & & & 1\end{array}\right]\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\begin{array}{@{}cccc@{}}1 & & p^{-1}x_{13} & p^{-1}x_{14}\\ & 1 & p^{-1}x_{23} & p^{-1}x_{24}\\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{24},x_{34}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}1 & & & \\ & p & & \\ & & p & x_{34}\\ & & & 1\end{array}\right]\left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & & p^{-1}x_{24}\\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{23}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}1 & & & \\ & p & & \\ & & 1 & \\ & & & p\end{array}\right]\left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & p^{-1}x_{23} & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{12},x_{14},x_{34}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\!\!\left[\begin{array}{@{}cccc@{}}p & x_{12} & & \\ & 1 & & \\ & & p & x_{34}\\ & & & 1\end{array}\right]\!\!\left[\begin{array}{@{}cccc@{}}1 & & & p^{-1}x_{14}\\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]\!K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{x_{12},x_{13}\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}\left[\begin{array}{@{}cccc@{}}p & x_{12} & & \\ & 1 & & \\ & & 1 & \\ & & & p\end{array}\right]\left[\begin{array}{@{}cccc@{}}1 & & p^{-1}x_{13} & \\ & 1 & & \\ & & 1 & \\ & & & 1\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \left[\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & & \\ & & p & \\ & & & p\end{array}\right]K_{p}.\nonumber\end{eqnarray}$$
We can now describe the actions of the Hecke operators defined by the ![]() $K_{p}hK_{p}$s above. With the invariant measure
$K_{p}hK_{p}$s above. With the invariant measure ![]() $dx$ of
$dx$ of ![]() ${\mathcal{G}}_{p}$ normalized so that
${\mathcal{G}}_{p}$ normalized so that 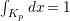 $\int _{K_{p}}dx=1$, we define
$\int _{K_{p}}dx=1$, we define 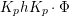 $K_{p}hK_{p}\cdot {\rm\Phi}$ by
$K_{p}hK_{p}\cdot {\rm\Phi}$ by
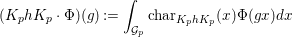 $$\begin{eqnarray}(K_{p}hK_{p}\cdot {\rm\Phi})(g):=\displaystyle \int _{{\mathcal{G}}_{p}}\operatorname{char}_{K_{p}hK_{p}}(x){\rm\Phi}(gx)dx\end{eqnarray}$$
$$\begin{eqnarray}(K_{p}hK_{p}\cdot {\rm\Phi})(g):=\displaystyle \int _{{\mathcal{G}}_{p}}\operatorname{char}_{K_{p}hK_{p}}(x){\rm\Phi}(gx)dx\end{eqnarray}$$ for 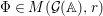 ${\rm\Phi}\in M({\mathcal{G}}(\mathbb{A}),r)$, where
${\rm\Phi}\in M({\mathcal{G}}(\mathbb{A}),r)$, where 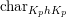 $\operatorname{char}_{K_{p}hK_{p}}$ denotes the characteristic function for
$\operatorname{char}_{K_{p}hK_{p}}$ denotes the characteristic function for ![]() $K_{p}hK_{p}$.
$K_{p}hK_{p}$.
We provide the nonadelic description of 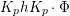 $K_{p}hK_{p}\cdot {\rm\Phi}$, which enables us to describe explicitly the influence of the
$K_{p}hK_{p}\cdot {\rm\Phi}$, which enables us to describe explicitly the influence of the ![]() $K_{p}hK_{p}$-action on Fourier coefficients of the lifting
$K_{p}hK_{p}$-action on Fourier coefficients of the lifting ![]() $F_{f}$.
$F_{f}$.
To this end we now introduce the sets
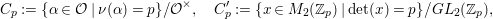 $$\begin{eqnarray}\displaystyle C_{p}:=\{{\it\alpha}\in {\mathcal{O}}\mid {\it\nu}({\it\alpha})=p\}/{\mathcal{O}}^{\times },\quad C_{p}^{\prime }:=\{x\in M_{2}(\mathbb{Z}_{p})\mid \det (x)=p\}/GL_{2}(\mathbb{Z}_{p}), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{p}:=\{{\it\alpha}\in {\mathcal{O}}\mid {\it\nu}({\it\alpha})=p\}/{\mathcal{O}}^{\times },\quad C_{p}^{\prime }:=\{x\in M_{2}(\mathbb{Z}_{p})\mid \det (x)=p\}/GL_{2}(\mathbb{Z}_{p}), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$and state the following lemma.
(1) There is a bijection
 $$\begin{eqnarray}C_{p}^{\prime }\simeq \left\{\left.\!\left[\begin{array}{@{}cc@{}}1 & 0\\ 0 & p\end{array}\right],~\left[\begin{array}{@{}cc@{}}p & b\\ 0 & 1\end{array}\right]\right|b\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}C_{p}^{\prime }\simeq \left\{\left.\!\left[\begin{array}{@{}cc@{}}1 & 0\\ 0 & p\end{array}\right],~\left[\begin{array}{@{}cc@{}}p & b\\ 0 & 1\end{array}\right]\right|b\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}\right\}.\end{eqnarray}$$(2) For an odd prime
 $p$, the isomorphism
$p$, the isomorphism  ${\mathcal{O}}_{p}\simeq M_{2}(\mathbb{Z}_{p})$ induces the bijection
${\mathcal{O}}_{p}\simeq M_{2}(\mathbb{Z}_{p})$ induces the bijection  $$\begin{eqnarray}C_{p}\simeq C_{p}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}C_{p}\simeq C_{p}^{\prime }.\end{eqnarray}$$
Proof. The first assertion is verified by a direct calculation. We prove the second assertion. As is remarked in the proof of [Reference Pitale22, Proposition 5.2], we have 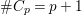 $\#C_{p}=p+1$. Under the isomorphism
$\#C_{p}=p+1$. Under the isomorphism 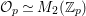 ${\mathcal{O}}_{p}\simeq M_{2}(\mathbb{Z}_{p})$, we can regard any element in
${\mathcal{O}}_{p}\simeq M_{2}(\mathbb{Z}_{p})$, we can regard any element in ![]() ${\mathcal{O}}$ as one lying in
${\mathcal{O}}$ as one lying in ![]() $M_{2}(\mathbb{Z}_{p})$. Any two inequivalent representatives of
$M_{2}(\mathbb{Z}_{p})$. Any two inequivalent representatives of ![]() $C_{p}$ are not equivalent to each other in
$C_{p}$ are not equivalent to each other in 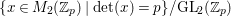 $\{x\in M_{2}(\mathbb{Z}_{p})\mid \det (x)=p\}/\text{GL}_{2}(\mathbb{Z}_{p})$. Otherwise there are two inequivalent representatives
$\{x\in M_{2}(\mathbb{Z}_{p})\mid \det (x)=p\}/\text{GL}_{2}(\mathbb{Z}_{p})$. Otherwise there are two inequivalent representatives ![]() ${\it\alpha}_{1}$ and
${\it\alpha}_{1}$ and ![]() ${\it\alpha}_{2}$ of
${\it\alpha}_{2}$ of ![]() $C_{p}$ which are equivalent under
$C_{p}$ which are equivalent under ![]() ${\mathcal{O}}_{l}^{\times }$-action for all primes
${\mathcal{O}}_{l}^{\times }$-action for all primes ![]() $l$, since
$l$, since 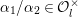 ${\it\alpha}_{1}/{\it\alpha}_{2}\in {\mathcal{O}}_{l}^{\times }$ for all primes
${\it\alpha}_{1}/{\it\alpha}_{2}\in {\mathcal{O}}_{l}^{\times }$ for all primes ![]() $l$. Note here that
$l$. Note here that 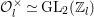 ${\mathcal{O}}_{l}^{\times }\simeq \text{GL}_{2}(\mathbb{Z}_{l})$ for any odd primes
${\mathcal{O}}_{l}^{\times }\simeq \text{GL}_{2}(\mathbb{Z}_{l})$ for any odd primes ![]() $l$. This, however, implies that two such representatives are equivalent to each other in
$l$. This, however, implies that two such representatives are equivalent to each other in ![]() $C_{p}$. We therefore know that there is a injection from
$C_{p}$. We therefore know that there is a injection from ![]() $C_{p}$ into
$C_{p}$ into 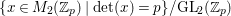 $\{x\in M_{2}(\mathbb{Z}_{p})\mid \det (x)=p\}/\text{GL}_{2}(\mathbb{Z}_{p})$. Since the latter set also has
$\{x\in M_{2}(\mathbb{Z}_{p})\mid \det (x)=p\}/\text{GL}_{2}(\mathbb{Z}_{p})$. Since the latter set also has ![]() $p+1$ representatives as in the statement, the injection is actually a bijection.◻
$p+1$ representatives as in the statement, the injection is actually a bijection.◻
Let 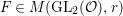 $F\in M(\text{GL}_{2}({\mathcal{O}}),r)$ correspond to
$F\in M(\text{GL}_{2}({\mathcal{O}}),r)$ correspond to ![]() ${\rm\Phi}$. By
${\rm\Phi}$. By 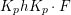 $K_{p}hK_{p}\cdot F$ we denote the cusp form in
$K_{p}hK_{p}\cdot F$ we denote the cusp form in 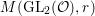 $M(\text{GL}_{2}({\mathcal{O}}),r)$ corresponding to
$M(\text{GL}_{2}({\mathcal{O}}),r)$ corresponding to 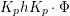 $K_{p}hK_{p}\cdot {\rm\Phi}$. Due to Lemma 2.3,
$K_{p}hK_{p}\cdot {\rm\Phi}$. Due to Lemma 2.3, 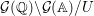 ${\mathcal{G}}(\mathbb{Q})\setminus {\mathcal{G}}(\mathbb{A})/U$ has a complete set of representatives in
${\mathcal{G}}(\mathbb{Q})\setminus {\mathcal{G}}(\mathbb{A})/U$ has a complete set of representatives in ![]() ${\mathcal{G}}(\mathbb{R})$, where
${\mathcal{G}}(\mathbb{R})$, where ![]() ${\mathcal{G}}(\mathbb{R})$ is viewed as a subgroup of
${\mathcal{G}}(\mathbb{R})$ is viewed as a subgroup of ![]() ${\mathcal{G}}(\mathbb{A})$ in the usual manner. The cusp form
${\mathcal{G}}(\mathbb{A})$ in the usual manner. The cusp form 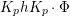 $K_{p}hK_{p}\cdot {\rm\Phi}$ is thereby determined by its restriction to
$K_{p}hK_{p}\cdot {\rm\Phi}$ is thereby determined by its restriction to ![]() ${\mathcal{G}}(\mathbb{R})$, which is nothing but
${\mathcal{G}}(\mathbb{R})$, which is nothing but 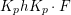 $K_{p}hK_{p}\cdot F$. Moreover, we remark that an element in
$K_{p}hK_{p}\cdot F$. Moreover, we remark that an element in 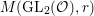 $M(\text{GL}_{2}({\mathcal{O}}),r)$ is determined by its restriction to
$M(\text{GL}_{2}({\mathcal{O}}),r)$ is determined by its restriction to 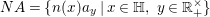 $NA=\{n(x)a_{y}\mid x\in \mathbb{H},~y\in \mathbb{R}_{+}^{\times }\}$ (see (2.1)).
$NA=\{n(x)a_{y}\mid x\in \mathbb{H},~y\in \mathbb{R}_{+}^{\times }\}$ (see (2.1)).
Proposition 5.7. Let  $K_{p}hK_{p}\cdot F$ be as above, and let
$K_{p}hK_{p}\cdot F$ be as above, and let ![]() $n(x)$ and
$n(x)$ and ![]() $a_{y}$ be as defined in (2.1). For
$a_{y}$ be as defined in (2.1). For ![]() $p$ odd, let
$p$ odd, let ![]() $C_{p}$ be as defined in (5.3).
$C_{p}$ be as defined in (5.3).
(1) Let
 $p=2$, and let
$p=2$, and let  $h=\left[\!\begin{smallmatrix}{\it\varpi}_{2} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]$. We have
$h=\left[\!\begin{smallmatrix}{\it\varpi}_{2} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]$. We have  $$\begin{eqnarray}(K_{2}hK_{2}\cdot F)(n(x)a_{y})=F(n({\it\varpi}_{2}x)a_{2^{1/2}y})+2^{2}F(n({\it\varpi}_{2}^{-1}x)a_{2^{-1/2}y}).\end{eqnarray}$$
$$\begin{eqnarray}(K_{2}hK_{2}\cdot F)(n(x)a_{y})=F(n({\it\varpi}_{2}x)a_{2^{1/2}y})+2^{2}F(n({\it\varpi}_{2}^{-1}x)a_{2^{-1/2}y}).\end{eqnarray}$$(2) Let
 $p\not =2$.
$p\not =2$.(a) When
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & p & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$, we have
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & p & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$, we have  $$\begin{eqnarray}\displaystyle (K_{p}hK_{p}\cdot F)(n(x)a_{y}) & = & \displaystyle \mathop{\sum }_{{\it\alpha}\in C_{p}}F(n({\it\alpha}x)a_{p^{1/2}y})\nonumber\\ \displaystyle & & \displaystyle +\,p^{2}\mathop{\sum }_{{\it\alpha}\in C_{p}}F(n(x{\it\alpha}^{-1})a_{p^{-1/2}y}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (K_{p}hK_{p}\cdot F)(n(x)a_{y}) & = & \displaystyle \mathop{\sum }_{{\it\alpha}\in C_{p}}F(n({\it\alpha}x)a_{p^{1/2}y})\nonumber\\ \displaystyle & & \displaystyle +\,p^{2}\mathop{\sum }_{{\it\alpha}\in C_{p}}F(n(x{\it\alpha}^{-1})a_{p^{-1/2}y}).\nonumber\end{eqnarray}$$(b) When
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & 1 & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$, we have
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & 1 & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$, we have  $$\begin{eqnarray}\displaystyle (K_{p}hK_{p}\cdot F)(n(x)a_{y}) & = & \displaystyle \mathop{\sum }_{{\it\alpha}\in C_{p}}F(n(x{\it\alpha})a_{p^{1/2}y})\nonumber\\ \displaystyle & & \displaystyle +\,p^{2}\mathop{\sum }_{{\it\alpha}\in C_{p}}F(n({\it\alpha}^{-1}x)a_{p^{-1/2}y}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (K_{p}hK_{p}\cdot F)(n(x)a_{y}) & = & \displaystyle \mathop{\sum }_{{\it\alpha}\in C_{p}}F(n(x{\it\alpha})a_{p^{1/2}y})\nonumber\\ \displaystyle & & \displaystyle +\,p^{2}\mathop{\sum }_{{\it\alpha}\in C_{p}}F(n({\it\alpha}^{-1}x)a_{p^{-1/2}y}).\nonumber\end{eqnarray}$$(c) When
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$, we have
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$, we have  $$\begin{eqnarray}\displaystyle (K_{p}hK_{p}\cdot F)(n(x)a_{y}) & = & \displaystyle F(n(px)a_{py})+p^{4}F(n(p^{-1}x)a_{p^{-1}y})\nonumber\\ \displaystyle & & \displaystyle +\,p\mathop{\sum }_{({\it\alpha}_{1},{\it\alpha}_{2})\in C_{p}\times C_{p}}F(n({\it\alpha}_{1}^{-1}x{\it\alpha}_{2})a_{y}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (K_{p}hK_{p}\cdot F)(n(x)a_{y}) & = & \displaystyle F(n(px)a_{py})+p^{4}F(n(p^{-1}x)a_{p^{-1}y})\nonumber\\ \displaystyle & & \displaystyle +\,p\mathop{\sum }_{({\it\alpha}_{1},{\it\alpha}_{2})\in C_{p}\times C_{p}}F(n({\it\alpha}_{1}^{-1}x{\it\alpha}_{2})a_{y}).\nonumber\end{eqnarray}$$
Proof. We prove only (2c). The other cases are settled similarly. We make use of the isomorphism 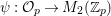 ${\it\psi}:{\mathcal{O}}_{p}\rightarrow M_{2}(\mathbb{Z}_{p})$, given explicitly as follows. Since
${\it\psi}:{\mathcal{O}}_{p}\rightarrow M_{2}(\mathbb{Z}_{p})$, given explicitly as follows. Since ![]() $p$ is odd, we can find
$p$ is odd, we can find 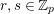 $r,s\in \mathbb{Z}_{p}$ such that
$r,s\in \mathbb{Z}_{p}$ such that 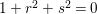 $1+r^{2}+s^{2}=0$. Then, we have
$1+r^{2}+s^{2}=0$. Then, we have
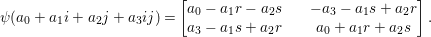 $$\begin{eqnarray}{\it\psi}(a_{0}+a_{1}i+a_{2}j+a_{3}ij)=\left[\begin{array}{@{}ccc@{}}a_{0}-a_{1}r-a_{2}s & & -a_{3}-a_{1}s+a_{2}r\\ a_{3}-a_{1}s+a_{2}r & & a_{0}+a_{1}r+a_{2}s\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}{\it\psi}(a_{0}+a_{1}i+a_{2}j+a_{3}ij)=\left[\begin{array}{@{}ccc@{}}a_{0}-a_{1}r-a_{2}s & & -a_{3}-a_{1}s+a_{2}r\\ a_{3}-a_{1}s+a_{2}r & & a_{0}+a_{1}r+a_{2}s\end{array}\right].\end{eqnarray}$$ Let 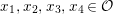 $x_{1},x_{2},x_{3},x_{4}\in {\mathcal{O}}$ such that
$x_{1},x_{2},x_{3},x_{4}\in {\mathcal{O}}$ such that
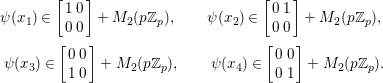 $$\begin{eqnarray}\displaystyle {\it\psi}(x_{1})\in \left[\begin{array}{@{}cc@{}}1 & 0\\ 0 & 0\end{array}\right]+M_{2}(p\mathbb{Z}_{p}),\qquad {\it\psi}(x_{2})\in \left[\begin{array}{@{}cc@{}}0 & 1\\ 0 & 0\end{array}\right]+M_{2}(p\mathbb{Z}_{p}), & & \displaystyle \nonumber\\ \displaystyle {\it\psi}(x_{3})\in \left[\begin{array}{@{}cc@{}}0 & 0\\ 1 & 0\end{array}\right]+M_{2}(p\mathbb{Z}_{p}),\qquad {\it\psi}(x_{4})\in \left[\begin{array}{@{}cc@{}}0 & 0\\ 0 & 1\end{array}\right]+M_{2}(p\mathbb{Z}_{p}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\psi}(x_{1})\in \left[\begin{array}{@{}cc@{}}1 & 0\\ 0 & 0\end{array}\right]+M_{2}(p\mathbb{Z}_{p}),\qquad {\it\psi}(x_{2})\in \left[\begin{array}{@{}cc@{}}0 & 1\\ 0 & 0\end{array}\right]+M_{2}(p\mathbb{Z}_{p}), & & \displaystyle \nonumber\\ \displaystyle {\it\psi}(x_{3})\in \left[\begin{array}{@{}cc@{}}0 & 0\\ 1 & 0\end{array}\right]+M_{2}(p\mathbb{Z}_{p}),\qquad {\it\psi}(x_{4})\in \left[\begin{array}{@{}cc@{}}0 & 0\\ 0 & 1\end{array}\right]+M_{2}(p\mathbb{Z}_{p}). & & \displaystyle \nonumber\end{eqnarray}$$ For example, let 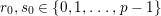 $r_{0},s_{0}\in \{0,1,\ldots ,p-1\}$ such that
$r_{0},s_{0}\in \{0,1,\ldots ,p-1\}$ such that 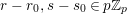 $r-r_{0},s-s_{0}\in p\mathbb{Z}_{p}$. Then, we can choose
$r-r_{0},s-s_{0}\in p\mathbb{Z}_{p}$. Then, we can choose 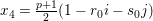 $x_{4}=\frac{p+1}{2}(1-r_{0}i-s_{0}j)$, where note that
$x_{4}=\frac{p+1}{2}(1-r_{0}i-s_{0}j)$, where note that 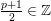 $\frac{p+1}{2}\in \mathbb{Z}$ since
$\frac{p+1}{2}\in \mathbb{Z}$ since ![]() $p$ is odd. Denote by
$p$ is odd. Denote by  ${\it\alpha}_{0},{\it\alpha}_{1},{\it\alpha}_{2},\ldots ,{\it\alpha}_{p}$ the representatives of
${\it\alpha}_{0},{\it\alpha}_{1},{\it\alpha}_{2},\ldots ,{\it\alpha}_{p}$ the representatives of ![]() $C_{p}$ such that
$C_{p}$ such that
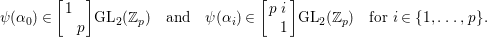 $$\begin{eqnarray}{\it\psi}({\it\alpha}_{0})\in \left[\begin{array}{@{}cc@{}}1 & \\ & p\end{array}\right]\text{GL}_{2}(\mathbb{Z}_{p})\quad \text{and}\quad {\it\psi}({\it\alpha}_{i})\in \left[\begin{array}{@{}cc@{}}p & i\\ & 1\end{array}\right]\text{GL}_{2}(\mathbb{Z}_{p})\quad \text{for }i\in \{1,\ldots ,p\}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\psi}({\it\alpha}_{0})\in \left[\begin{array}{@{}cc@{}}1 & \\ & p\end{array}\right]\text{GL}_{2}(\mathbb{Z}_{p})\quad \text{and}\quad {\it\psi}({\it\alpha}_{i})\in \left[\begin{array}{@{}cc@{}}p & i\\ & 1\end{array}\right]\text{GL}_{2}(\mathbb{Z}_{p})\quad \text{for }i\in \{1,\ldots ,p\}.\end{eqnarray}$$ The left coset decomposition of ![]() $K_{p}hK_{p}$ in part (2c) of Lemma 5.5 can be rewritten as
$K_{p}hK_{p}$ in part (2c) of Lemma 5.5 can be rewritten as
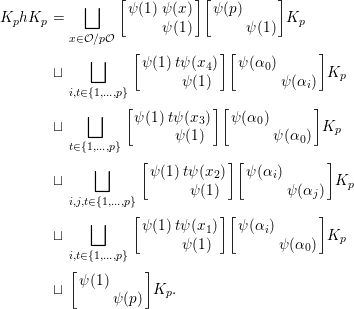 $$\begin{eqnarray}\displaystyle K_{p}hK_{p} & = & \displaystyle \mathop{\sqcup }_{x\in {\mathcal{O}}/p{\mathcal{O}}}\left[\begin{array}{@{}cc@{}}{\it\psi}(1) & {\it\psi}(x)\\ & {\it\psi}(1)\end{array}\right]\left[\begin{array}{@{}cc@{}}{\it\psi}(p) & \\ & {\it\psi}(1)\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{i,t\in \{1,\ldots ,p\}}\left[\begin{array}{@{}cc@{}}{\it\psi}(1) & t{\it\psi}(x_{4})\\ & {\it\psi}(1)\end{array}\right]\left[\begin{array}{@{}cc@{}}{\it\psi}({\it\alpha}_{0}) & \\ & {\it\psi}({\it\alpha}_{i})\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{t\in \{1,\ldots ,p\}}\left[\begin{array}{@{}cc@{}}{\it\psi}(1) & t{\it\psi}(x_{3})\\ & {\it\psi}(1)\end{array}\right]\left[\begin{array}{@{}cc@{}}{\it\psi}({\it\alpha}_{0}) & \\ & {\it\psi}({\it\alpha}_{0})\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{i,j,t\in \{1,\ldots ,p\}}\left[\begin{array}{@{}cc@{}}{\it\psi}(1) & t{\it\psi}(x_{2})\\ & {\it\psi}(1)\end{array}\right]\left[\begin{array}{@{}cc@{}}{\it\psi}({\it\alpha}_{i}) & \\ & {\it\psi}({\it\alpha}_{j})\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{i,t\in \{1,\ldots ,p\}}\left[\begin{array}{@{}cc@{}}{\it\psi}(1) & t{\it\psi}(x_{1})\\ & {\it\psi}(1)\end{array}\right]\left[\begin{array}{@{}cc@{}}{\it\psi}({\it\alpha}_{i}) & \\ & {\it\psi}({\it\alpha}_{0})\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \left[\begin{array}{@{}cc@{}}{\it\psi}(1) & \\ & {\it\psi}(p)\end{array}\right]K_{p}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{p}hK_{p} & = & \displaystyle \mathop{\sqcup }_{x\in {\mathcal{O}}/p{\mathcal{O}}}\left[\begin{array}{@{}cc@{}}{\it\psi}(1) & {\it\psi}(x)\\ & {\it\psi}(1)\end{array}\right]\left[\begin{array}{@{}cc@{}}{\it\psi}(p) & \\ & {\it\psi}(1)\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{i,t\in \{1,\ldots ,p\}}\left[\begin{array}{@{}cc@{}}{\it\psi}(1) & t{\it\psi}(x_{4})\\ & {\it\psi}(1)\end{array}\right]\left[\begin{array}{@{}cc@{}}{\it\psi}({\it\alpha}_{0}) & \\ & {\it\psi}({\it\alpha}_{i})\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{t\in \{1,\ldots ,p\}}\left[\begin{array}{@{}cc@{}}{\it\psi}(1) & t{\it\psi}(x_{3})\\ & {\it\psi}(1)\end{array}\right]\left[\begin{array}{@{}cc@{}}{\it\psi}({\it\alpha}_{0}) & \\ & {\it\psi}({\it\alpha}_{0})\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{i,j,t\in \{1,\ldots ,p\}}\left[\begin{array}{@{}cc@{}}{\it\psi}(1) & t{\it\psi}(x_{2})\\ & {\it\psi}(1)\end{array}\right]\left[\begin{array}{@{}cc@{}}{\it\psi}({\it\alpha}_{i}) & \\ & {\it\psi}({\it\alpha}_{j})\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \mathop{\sqcup }_{i,t\in \{1,\ldots ,p\}}\left[\begin{array}{@{}cc@{}}{\it\psi}(1) & t{\it\psi}(x_{1})\\ & {\it\psi}(1)\end{array}\right]\left[\begin{array}{@{}cc@{}}{\it\psi}({\it\alpha}_{i}) & \\ & {\it\psi}({\it\alpha}_{0})\end{array}\right]K_{p}\nonumber\\ \displaystyle & \sqcup & \displaystyle \left[\begin{array}{@{}cc@{}}{\it\psi}(1) & \\ & {\it\psi}(p)\end{array}\right]K_{p}.\nonumber\end{eqnarray}$$ We note that 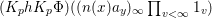 $(K_{p}hK_{p}{\rm\Phi})((n(x)a_{y})_{\infty }\prod _{v<\infty }1_{v})$ is the sum of terms of the form
$(K_{p}hK_{p}{\rm\Phi})((n(x)a_{y})_{\infty }\prod _{v<\infty }1_{v})$ is the sum of terms of the form 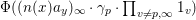 ${\rm\Phi}((n(x)a_{y})_{\infty }\cdot {\it\gamma}_{p}\cdot \prod _{v\neq p,\infty }1_{v})$, where
${\rm\Phi}((n(x)a_{y})_{\infty }\cdot {\it\gamma}_{p}\cdot \prod _{v\neq p,\infty }1_{v})$, where ![]() ${\it\gamma}_{p}$ runs over the single coset representatives above. Since we have chosen the coset representatives
${\it\gamma}_{p}$ runs over the single coset representatives above. Since we have chosen the coset representatives ![]() ${\it\gamma}_{p}$ above in
${\it\gamma}_{p}$ above in ![]() $M_{2}({\mathcal{O}})$,
$M_{2}({\mathcal{O}})$, 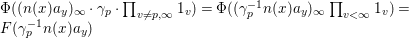 ${\rm\Phi}((n(x)a_{y})_{\infty }\cdot {\it\gamma}_{p}\cdot \prod _{v\neq p,\infty }1_{v})={\rm\Phi}(({\it\gamma}_{p}^{-1}n(x)a_{y})_{\infty }\prod _{v<\infty }1_{v})=F({\it\gamma}_{p}^{-1}n(x)a_{y})$. Here, we have used the left
${\rm\Phi}((n(x)a_{y})_{\infty }\cdot {\it\gamma}_{p}\cdot \prod _{v\neq p,\infty }1_{v})={\rm\Phi}(({\it\gamma}_{p}^{-1}n(x)a_{y})_{\infty }\prod _{v<\infty }1_{v})=F({\it\gamma}_{p}^{-1}n(x)a_{y})$. Here, we have used the left ![]() ${\mathcal{G}}(\mathbb{Q})$-invariance and right
${\mathcal{G}}(\mathbb{Q})$-invariance and right ![]() $K_{v}$-invariance of
$K_{v}$-invariance of ![]() ${\rm\Phi}$.
${\rm\Phi}$.
Next, we substitute the Fourier expansion of ![]() $F$ and perform an appropriate change of variable for
$F$ and perform an appropriate change of variable for ![]() ${\it\beta}$ to get the proposition. Note that, for the first set of left cosets, we have to use that
${\it\beta}$ to get the proposition. Note that, for the first set of left cosets, we have to use that 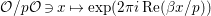 ${\mathcal{O}}/p{\mathcal{O}}\ni x\mapsto \exp (2{\it\pi}i\operatorname{Re}({\it\beta}x/p))$ is a nontrivial character of
${\mathcal{O}}/p{\mathcal{O}}\ni x\mapsto \exp (2{\it\pi}i\operatorname{Re}({\it\beta}x/p))$ is a nontrivial character of 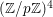 $(\mathbb{Z}/p\mathbb{Z})^{4}$ if and only if
$(\mathbb{Z}/p\mathbb{Z})^{4}$ if and only if ![]() $p$ does not divide
$p$ does not divide ![]() ${\it\beta}$.◻
${\it\beta}$.◻
For this proposition we remark that the formulas above do not depend on the choices of representatives of ![]() $C_{p}$, since
$C_{p}$, since ![]() $F$ is left- and right-invariant with respect to
$F$ is left- and right-invariant with respect to 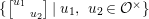 $\{\left[\!\begin{smallmatrix}u_{1} & \phantom{}\\ & u_{2}\end{smallmatrix}\!\right]\mid u_{1},~u_{2}\in {\mathcal{O}}^{\times }\}$. Let the Fourier decomposition of
$\{\left[\!\begin{smallmatrix}u_{1} & \phantom{}\\ & u_{2}\end{smallmatrix}\!\right]\mid u_{1},~u_{2}\in {\mathcal{O}}^{\times }\}$. Let the Fourier decomposition of 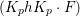 $(K_{p}hK_{p}\cdot F)$ be given by
$(K_{p}hK_{p}\cdot F)$ be given by
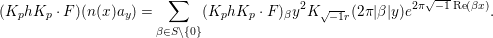 $$\begin{eqnarray}(K_{p}hK_{p}\cdot F)(n(x)a_{y})=\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}(K_{p}hK_{p}\cdot F)_{{\it\beta}}y^{2}K_{\sqrt{-1}r}(2{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{Re}({\it\beta}x)}.\end{eqnarray}$$
$$\begin{eqnarray}(K_{p}hK_{p}\cdot F)(n(x)a_{y})=\mathop{\sum }_{{\it\beta}\in S\setminus \{0\}}(K_{p}hK_{p}\cdot F)_{{\it\beta}}y^{2}K_{\sqrt{-1}r}(2{\it\pi}|{\it\beta}|y)e^{2{\it\pi}\sqrt{-1}\operatorname{Re}({\it\beta}x)}.\end{eqnarray}$$ The next proposition provides a formula for 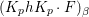 $(K_{p}hK_{p}\cdot F)_{{\it\beta}}$ in terms of the Fourier coefficients
$(K_{p}hK_{p}\cdot F)_{{\it\beta}}$ in terms of the Fourier coefficients ![]() $A({\it\beta})$ of
$A({\it\beta})$ of ![]() $F$.
$F$.
(1) Let
 $p=2$, and let
$p=2$, and let  $h=\left[\!\begin{smallmatrix}{\it\varpi}_{2} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]$. We obtain
$h=\left[\!\begin{smallmatrix}{\it\varpi}_{2} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right]$. We obtain  $$\begin{eqnarray}(K_{2}hK_{2}\cdot F)_{{\it\beta}}=2(A({\it\beta}{\it\varpi}_{2}^{-1})+A({\it\beta}{\it\varpi}_{2})).\end{eqnarray}$$
$$\begin{eqnarray}(K_{2}hK_{2}\cdot F)_{{\it\beta}}=2(A({\it\beta}{\it\varpi}_{2}^{-1})+A({\it\beta}{\it\varpi}_{2})).\end{eqnarray}$$(2) Let
 $p$ be an odd prime, and let
$p$ be an odd prime, and let  ${\it\beta}\in S\setminus \{0\}$.
${\it\beta}\in S\setminus \{0\}$.(a) When
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & p & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$,
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & p & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$,  $$\begin{eqnarray}(K_{p}hK_{p}\cdot F)_{{\it\beta}}=p\left(\mathop{\sum }_{{\it\alpha}\in C_{p}}A({\it\beta}\bar{{\it\alpha}}^{-1})+\mathop{\sum }_{{\it\alpha}\in C_{p}}A(\bar{{\it\alpha}}{\it\beta})\right).\end{eqnarray}$$
$$\begin{eqnarray}(K_{p}hK_{p}\cdot F)_{{\it\beta}}=p\left(\mathop{\sum }_{{\it\alpha}\in C_{p}}A({\it\beta}\bar{{\it\alpha}}^{-1})+\mathop{\sum }_{{\it\alpha}\in C_{p}}A(\bar{{\it\alpha}}{\it\beta})\right).\end{eqnarray}$$(b) When
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & 1 & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$,
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & 1 & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$,  $$\begin{eqnarray}(K_{p}hK_{p}\cdot F)_{{\it\beta}}=p\left(\mathop{\sum }_{{\it\alpha}\in C_{p}}A({\it\alpha}^{-1}{\it\beta})+\mathop{\sum }_{{\it\alpha}\in C_{p}}A({\it\beta}{\it\alpha})\right).\end{eqnarray}$$
$$\begin{eqnarray}(K_{p}hK_{p}\cdot F)_{{\it\beta}}=p\left(\mathop{\sum }_{{\it\alpha}\in C_{p}}A({\it\alpha}^{-1}{\it\beta})+\mathop{\sum }_{{\it\alpha}\in C_{p}}A({\it\beta}{\it\alpha})\right).\end{eqnarray}$$(c) When
 $h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$,
$h=\left[\!\begin{smallmatrix}p & & & \phantom{}\\ & p & & \phantom{}\\ & & 1 & \phantom{}\\ & & & 1\end{smallmatrix}\!\right]$,  $$\begin{eqnarray}\displaystyle (K_{p}hK_{p}\cdot F)_{{\it\beta}} & = & \displaystyle p^{2}(A(p^{-1}{\it\beta})+A(p{\it\beta}))\nonumber\\ \displaystyle & & \displaystyle +\,p\mathop{\sum }_{({\it\alpha}_{1},{\it\alpha}_{2})\in C_{p}\times C_{p}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (K_{p}hK_{p}\cdot F)_{{\it\beta}} & = & \displaystyle p^{2}(A(p^{-1}{\it\beta})+A(p{\it\beta}))\nonumber\\ \displaystyle & & \displaystyle +\,p\mathop{\sum }_{({\it\alpha}_{1},{\it\alpha}_{2})\in C_{p}\times C_{p}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2}).\nonumber\end{eqnarray}$$
For this proposition we note that the automorphy of ![]() $F$ with respect to
$F$ with respect to 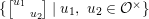 $\{\left[\!\begin{smallmatrix}u_{1} & \phantom{}\\ & u_{2}\end{smallmatrix}\!\right]\mid u_{1},~u_{2}\in {\mathcal{O}}^{\times }\}$ implies
$\{\left[\!\begin{smallmatrix}u_{1} & \phantom{}\\ & u_{2}\end{smallmatrix}\!\right]\mid u_{1},~u_{2}\in {\mathcal{O}}^{\times }\}$ implies 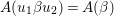 $A(u_{1}{\it\beta}u_{2})=A({\it\beta})$ for
$A(u_{1}{\it\beta}u_{2})=A({\it\beta})$ for 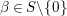 ${\it\beta}\in S\setminus \{0\}$ and
${\it\beta}\in S\setminus \{0\}$ and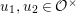 $u_{1},u_{2}\in {\mathcal{O}}^{\times }$. From this we see that the formulas in (2b) and (2c) do not depend on the choices of representatives for
$u_{1},u_{2}\in {\mathcal{O}}^{\times }$. From this we see that the formulas in (2b) and (2c) do not depend on the choices of representatives for ![]() $C_{p}$. For (2a) we furthermore see that, given any complete set
$C_{p}$. For (2a) we furthermore see that, given any complete set 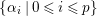 $\{{\it\alpha}_{i}\mid 0\leqslant i\leqslant p\}$ of representatives for
$\{{\it\alpha}_{i}\mid 0\leqslant i\leqslant p\}$ of representatives for ![]() $C_{p}$,
$C_{p}$, 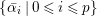 $\{\bar{{\it\alpha}_{i}}\mid 0\leqslant i\leqslant p\}$ also forms such a set. As a result, we see that the formula in (2a) is also not dependent on the choices of representatives for
$\{\bar{{\it\alpha}_{i}}\mid 0\leqslant i\leqslant p\}$ also forms such a set. As a result, we see that the formula in (2a) is also not dependent on the choices of representatives for ![]() $C_{p}$.
$C_{p}$.
5.3 Hecke equivariance for  $p=2$
$p=2$
Let 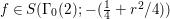 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a new form (for the definition see [Reference Iwaniec12, §8.5]) with Hecke eigenvalue
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a new form (for the definition see [Reference Iwaniec12, §8.5]) with Hecke eigenvalue ![]() ${\it\lambda}_{p}$ for
${\it\lambda}_{p}$ for ![]() $p=2$. By the Hecke eigenvalue
$p=2$. By the Hecke eigenvalue ![]() ${\it\lambda}_{2}$ we mean the eigenvalue of
${\it\lambda}_{2}$ we mean the eigenvalue of ![]() $f$ for the
$f$ for the ![]() $U(2)$ operator defined by the action of the double coset
$U(2)$ operator defined by the action of the double coset 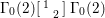 ${\rm\Gamma}_{0}(2)\left[\begin{smallmatrix}1 & \\ & 2\end{smallmatrix}\right]\,{\rm\Gamma}_{0}(2)$. Let us also assume that
${\rm\Gamma}_{0}(2)\left[\begin{smallmatrix}1 & \\ & 2\end{smallmatrix}\right]\,{\rm\Gamma}_{0}(2)$. Let us also assume that ![]() $f$ is an eigenfunction of the Atkin–Lehner involution with eigenvalue
$f$ is an eigenfunction of the Atkin–Lehner involution with eigenvalue ![]() ${\it\epsilon}$. It can be checked that
${\it\epsilon}$. It can be checked that ![]() ${\it\lambda}_{2}$ and
${\it\lambda}_{2}$ and ![]() ${\it\epsilon}$ are related by
${\it\epsilon}$ are related by
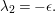 $$\begin{eqnarray}{\it\lambda}_{2}=-{\it\epsilon}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\lambda}_{2}=-{\it\epsilon}.\end{eqnarray}$$Using the single coset decomposition
 $$\begin{eqnarray}{\rm\Gamma}_{0}(2)\left[\begin{array}{@{}cc@{}}1 & \\ & 2\end{array}\right]{\rm\Gamma}_{0}(2)={\rm\Gamma}_{0}(2)\left[\begin{array}{@{}cc@{}}1 & 1\\ & 2\end{array}\right]\sqcup {\rm\Gamma}_{0}(2)\left[\begin{array}{@{}cc@{}}1 & \\ & 2\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Gamma}_{0}(2)\left[\begin{array}{@{}cc@{}}1 & \\ & 2\end{array}\right]{\rm\Gamma}_{0}(2)={\rm\Gamma}_{0}(2)\left[\begin{array}{@{}cc@{}}1 & 1\\ & 2\end{array}\right]\sqcup {\rm\Gamma}_{0}(2)\left[\begin{array}{@{}cc@{}}1 & \\ & 2\end{array}\right],\end{eqnarray}$$we get
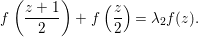 $$\begin{eqnarray}f\left(\frac{z+1}{2}\right)+f\left(\frac{z}{2}\right)={\it\lambda}_{2}f(z).\end{eqnarray}$$
$$\begin{eqnarray}f\left(\frac{z+1}{2}\right)+f\left(\frac{z}{2}\right)={\it\lambda}_{2}f(z).\end{eqnarray}$$ In terms of Fourier coefficients of ![]() $f$, using (5.5), we get
$f$, using (5.5), we get
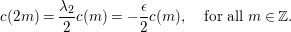 $$\begin{eqnarray}c(2m)=\frac{{\it\lambda}_{2}}{2}c(m)=-\frac{{\it\epsilon}}{2}c(m),\quad \text{for all }m\in \mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}c(2m)=\frac{{\it\lambda}_{2}}{2}c(m)=-\frac{{\it\epsilon}}{2}c(m),\quad \text{for all }m\in \mathbb{Z}.\end{eqnarray}$$Proposition 5.9. Let 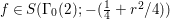 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a new form and an eigenfunction of the Atkin–Lehner involution with eigenvalue
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a new form and an eigenfunction of the Atkin–Lehner involution with eigenvalue ![]() ${\it\epsilon}$. Let
${\it\epsilon}$. Let ![]() $F=F_{f}$ be as defined in Theorem 4.4. Then,
$F=F_{f}$ be as defined in Theorem 4.4. Then,
 $$\begin{eqnarray}\left(K_{2}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & \\ & 1\end{array}\right]K_{2}\right)F=-3\sqrt{2}{\it\epsilon}F.\end{eqnarray}$$
$$\begin{eqnarray}\left(K_{2}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & \\ & 1\end{array}\right]K_{2}\right)F=-3\sqrt{2}{\it\epsilon}F.\end{eqnarray}$$Proof. Let 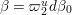 ${\it\beta}={\it\varpi}_{2}^{u}d{\it\beta}_{0}$ be a decomposition according to Proposition 4.2. Hence,
${\it\beta}={\it\varpi}_{2}^{u}d{\it\beta}_{0}$ be a decomposition according to Proposition 4.2. Hence, 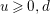 $u\geqslant 0,d$ is odd and
$u\geqslant 0,d$ is odd and 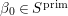 ${\it\beta}_{0}\in S^{\text{prim}}$. Using (5.5) and (5.6), we see that
${\it\beta}_{0}\in S^{\text{prim}}$. Using (5.5) and (5.6), we see that
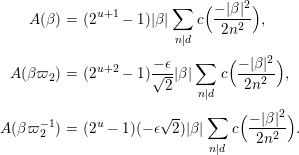 $$\begin{eqnarray}\displaystyle A({\it\beta}) & = & \displaystyle (2^{u+1}-1)|{\it\beta}|\mathop{\sum }_{n|d}c\Big(\frac{-|{\it\beta}|^{2}}{2n^{2}}\Big),\nonumber\\ \displaystyle A({\it\beta}{\it\varpi}_{2}) & = & \displaystyle (2^{u+2}-1)\frac{-{\it\epsilon}}{\sqrt{2}}|{\it\beta}|\mathop{\sum }_{n|d}c\Big(\frac{-|{\it\beta}|^{2}}{2n^{2}}\Big),\nonumber\\ \displaystyle A({\it\beta}{\it\varpi}_{2}^{-1}) & = & \displaystyle (2^{u}-1)(-{\it\epsilon}\sqrt{2})|{\it\beta}|\mathop{\sum }_{n|d}c\Big(\frac{-|{\it\beta}|^{2}}{2n^{2}}\Big).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A({\it\beta}) & = & \displaystyle (2^{u+1}-1)|{\it\beta}|\mathop{\sum }_{n|d}c\Big(\frac{-|{\it\beta}|^{2}}{2n^{2}}\Big),\nonumber\\ \displaystyle A({\it\beta}{\it\varpi}_{2}) & = & \displaystyle (2^{u+2}-1)\frac{-{\it\epsilon}}{\sqrt{2}}|{\it\beta}|\mathop{\sum }_{n|d}c\Big(\frac{-|{\it\beta}|^{2}}{2n^{2}}\Big),\nonumber\\ \displaystyle A({\it\beta}{\it\varpi}_{2}^{-1}) & = & \displaystyle (2^{u}-1)(-{\it\epsilon}\sqrt{2})|{\it\beta}|\mathop{\sum }_{n|d}c\Big(\frac{-|{\it\beta}|^{2}}{2n^{2}}\Big).\nonumber\end{eqnarray}$$ Note that, if ![]() $u=0$, then
$u=0$, then 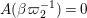 $A({\it\beta}{\it\varpi}_{2}^{-1})=0$, and so is the right-hand side of the third equality above. We have
$A({\it\beta}{\it\varpi}_{2}^{-1})=0$, and so is the right-hand side of the third equality above. We have
 $$\begin{eqnarray}\frac{2^{u+2}-1}{\sqrt{2}}+(2^{u}-1)\sqrt{2}=\frac{3}{\sqrt{2}}(2^{u+1}-1).\end{eqnarray}$$
$$\begin{eqnarray}\frac{2^{u+2}-1}{\sqrt{2}}+(2^{u}-1)\sqrt{2}=\frac{3}{\sqrt{2}}(2^{u+1}-1).\end{eqnarray}$$Hence, we have
 $$\begin{eqnarray}2(A({\it\beta}{\it\varpi}_{2})+A({\it\beta}{\it\varpi}_{2}^{-1}))=-3\sqrt{2}{\it\epsilon}A({\it\beta}).\end{eqnarray}$$
$$\begin{eqnarray}2(A({\it\beta}{\it\varpi}_{2})+A({\it\beta}{\it\varpi}_{2}^{-1}))=-3\sqrt{2}{\it\epsilon}A({\it\beta}).\end{eqnarray}$$The proposition now follows from part (1) of Proposition 5.8. ◻
5.4 Hecke equivariance for odd primes
We assume that 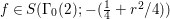 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ is a Hecke eigenform with Hecke eigenvalue
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ is a Hecke eigenform with Hecke eigenvalue ![]() ${\it\lambda}_{p}$ for every odd prime
${\it\lambda}_{p}$ for every odd prime ![]() $p$, but do not assume that
$p$, but do not assume that ![]() $f$ is a new form. In terms of Fourier coefficients of
$f$ is a new form. In terms of Fourier coefficients of ![]() $f$, the Hecke relation is given by
$f$, the Hecke relation is given by
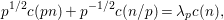 $$\begin{eqnarray}p^{1/2}c(pn)+p^{-1/2}c(n/p)={\it\lambda}_{p}c(n),\end{eqnarray}$$
$$\begin{eqnarray}p^{1/2}c(pn)+p^{-1/2}c(n/p)={\it\lambda}_{p}c(n),\end{eqnarray}$$ where ![]() $c(n/p)$ is assumed to be zero if
$c(n/p)$ is assumed to be zero if ![]() $p$ does not divide
$p$ does not divide ![]() $n$. The following lemma will play a key role in the computation of the Hecke operator.
$n$. The following lemma will play a key role in the computation of the Hecke operator.
Lemma 5.10. Let 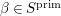 ${\it\beta}\in S^{\text{prim}}$. Then,
${\it\beta}\in S^{\text{prim}}$. Then,
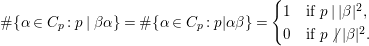 $$\begin{eqnarray}\#\{{\it\alpha}\in C_{p}:p\mid {\it\beta}{\it\alpha}\}=\#\{{\it\alpha}\in C_{p}:p|{\it\alpha}{\it\beta}\}=\left\{\begin{array}{@{}l@{}}1\quad \text{if }p\,|\,|{\it\beta}|^{2},\quad \\ 0\quad \text{if }p\not |\,|{\it\beta}|^{2}.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\#\{{\it\alpha}\in C_{p}:p\mid {\it\beta}{\it\alpha}\}=\#\{{\it\alpha}\in C_{p}:p|{\it\alpha}{\it\beta}\}=\left\{\begin{array}{@{}l@{}}1\quad \text{if }p\,|\,|{\it\beta}|^{2},\quad \\ 0\quad \text{if }p\not |\,|{\it\beta}|^{2}.\quad \end{array}\right.\end{eqnarray}$$ In addition, ![]() $p^{2}$ does not divide
$p^{2}$ does not divide ![]() ${\it\alpha}{\it\beta}$ or
${\it\alpha}{\it\beta}$ or ![]() ${\it\beta}{\it\alpha}$ for any
${\it\beta}{\it\alpha}$ for any ![]() ${\it\alpha}\in C_{p}$.
${\it\alpha}\in C_{p}$.
Proof. Note that, by taking conjugates, it is enough to prove the statement of the lemma for 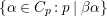 $\{{\it\alpha}\in C_{p}:p\mid {\it\beta}{\it\alpha}\}$ for all
$\{{\it\alpha}\in C_{p}:p\mid {\it\beta}{\it\alpha}\}$ for all ![]() ${\it\beta}$. Taking norms, it is clear that
${\it\beta}$. Taking norms, it is clear that ![]() $p$ does not divide
$p$ does not divide ![]() ${\it\beta}{\it\alpha}$ if
${\it\beta}{\it\alpha}$ if ![]() $p$ does not divide
$p$ does not divide ![]() $|{\it\beta}|^{2}$. Hence, assume that
$|{\it\beta}|^{2}$. Hence, assume that ![]() $p$ divides
$p$ divides ![]() $|{\it\beta}|^{2}$. Let
$|{\it\beta}|^{2}$. Let 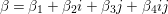 ${\it\beta}={\it\beta}_{1}+{\it\beta}_{2}i+{\it\beta}_{3}j+{\it\beta}_{4}ij$. The conditions
${\it\beta}={\it\beta}_{1}+{\it\beta}_{2}i+{\it\beta}_{3}j+{\it\beta}_{4}ij$. The conditions ![]() $p||{\it\beta}|^{2}$ and
$p||{\it\beta}|^{2}$ and ![]() $p\not |\,{\it\beta}$, imply that there is a pair amongst the set
$p\not |\,{\it\beta}$, imply that there is a pair amongst the set 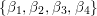 $\{{\it\beta}_{1},{\it\beta}_{2},{\it\beta}_{3},{\it\beta}_{4}\}$ which does not satisfy
$\{{\it\beta}_{1},{\it\beta}_{2},{\it\beta}_{3},{\it\beta}_{4}\}$ which does not satisfy 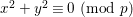 $x^{2}+y^{2}\equiv 0~(\text{mod}~p)$. From the proof it will be clear that we can take, without loss of generality,
$x^{2}+y^{2}\equiv 0~(\text{mod}~p)$. From the proof it will be clear that we can take, without loss of generality, 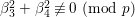 ${\it\beta}_{3}^{2}+{\it\beta}_{4}^{2}\not \equiv 0~(\text{mod}~p)$. Let
${\it\beta}_{3}^{2}+{\it\beta}_{4}^{2}\not \equiv 0~(\text{mod}~p)$. Let 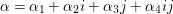 ${\it\alpha}={\it\alpha}_{1}+{\it\alpha}_{2}i+{\it\alpha}_{3}j+{\it\alpha}_{4}ij$. The condition
${\it\alpha}={\it\alpha}_{1}+{\it\alpha}_{2}i+{\it\alpha}_{3}j+{\it\alpha}_{4}ij$. The condition ![]() $p|{\it\beta}{\it\alpha}$ is equivalent to the following matrix equation modulo
$p|{\it\beta}{\it\alpha}$ is equivalent to the following matrix equation modulo ![]() $p$:
$p$:
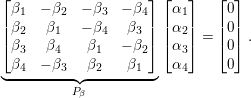 $$\begin{eqnarray}\underbrace{\left[\begin{array}{@{}cccc@{}}{\it\beta}_{1} & -{\it\beta}_{2} & -{\it\beta}_{3} & -{\it\beta}_{4}\\ {\it\beta}_{2} & {\it\beta}_{1} & -{\it\beta}_{4} & {\it\beta}_{3}\\ {\it\beta}_{3} & {\it\beta}_{4} & {\it\beta}_{1} & -{\it\beta}_{2}\\ {\it\beta}_{4} & -{\it\beta}_{3} & {\it\beta}_{2} & {\it\beta}_{1}\end{array}\right]}_{P_{{\it\beta}}}\left[\begin{array}{@{}c@{}}{\it\alpha}_{1}\\ {\it\alpha}_{2}\\ {\it\alpha}_{3}\\ {\it\alpha}_{4}\end{array}\right]=\left[\begin{array}{@{}c@{}}0\\ 0\\ 0\\ 0\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\underbrace{\left[\begin{array}{@{}cccc@{}}{\it\beta}_{1} & -{\it\beta}_{2} & -{\it\beta}_{3} & -{\it\beta}_{4}\\ {\it\beta}_{2} & {\it\beta}_{1} & -{\it\beta}_{4} & {\it\beta}_{3}\\ {\it\beta}_{3} & {\it\beta}_{4} & {\it\beta}_{1} & -{\it\beta}_{2}\\ {\it\beta}_{4} & -{\it\beta}_{3} & {\it\beta}_{2} & {\it\beta}_{1}\end{array}\right]}_{P_{{\it\beta}}}\left[\begin{array}{@{}c@{}}{\it\alpha}_{1}\\ {\it\alpha}_{2}\\ {\it\alpha}_{3}\\ {\it\alpha}_{4}\end{array}\right]=\left[\begin{array}{@{}c@{}}0\\ 0\\ 0\\ 0\end{array}\right].\end{eqnarray}$$ The matrix ![]() $P_{{\it\beta}}$ considered over
$P_{{\it\beta}}$ considered over ![]() $\mathbb{Z}_{p}$ has rank
$\mathbb{Z}_{p}$ has rank ![]() $2$. By our assumption
$2$. By our assumption 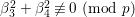 ${\it\beta}_{3}^{2}+{\it\beta}_{4}^{2}\not \equiv 0~(\text{mod}~p)$, we see that the kernel of
${\it\beta}_{3}^{2}+{\it\beta}_{4}^{2}\not \equiv 0~(\text{mod}~p)$, we see that the kernel of ![]() $P_{{\it\beta}}$ is spanned by the first two rows of
$P_{{\it\beta}}$ is spanned by the first two rows of ![]() $P_{{\it\beta}}$. Hence,
$P_{{\it\beta}}$. Hence, ![]() ${\it\alpha}$ is given by
${\it\alpha}$ is given by
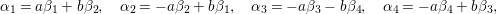 $$\begin{eqnarray}{\it\alpha}_{1}=a{\it\beta}_{1}+b{\it\beta}_{2},\quad {\it\alpha}_{2}=-a{\it\beta}_{2}+b{\it\beta}_{1},\quad {\it\alpha}_{3}=-a{\it\beta}_{3}-b{\it\beta}_{4},\quad {\it\alpha}_{4}=-a{\it\beta}_{4}+b{\it\beta}_{3},\end{eqnarray}$$
$$\begin{eqnarray}{\it\alpha}_{1}=a{\it\beta}_{1}+b{\it\beta}_{2},\quad {\it\alpha}_{2}=-a{\it\beta}_{2}+b{\it\beta}_{1},\quad {\it\alpha}_{3}=-a{\it\beta}_{3}-b{\it\beta}_{4},\quad {\it\alpha}_{4}=-a{\it\beta}_{4}+b{\it\beta}_{3},\end{eqnarray}$$ for some 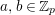 $a,b\in \mathbb{Z}_{p}$. This gives us
$a,b\in \mathbb{Z}_{p}$. This gives us 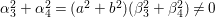 ${\it\alpha}_{3}^{2}+{\it\alpha}_{4}^{2}=(a^{2}+b^{2})({\it\beta}_{3}^{2}+{\it\beta}_{4}^{2})\neq 0$. This is because, by assumption,
${\it\alpha}_{3}^{2}+{\it\alpha}_{4}^{2}=(a^{2}+b^{2})({\it\beta}_{3}^{2}+{\it\beta}_{4}^{2})\neq 0$. This is because, by assumption, 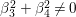 ${\it\beta}_{3}^{2}+{\it\beta}_{4}^{2}\neq 0$, and
${\it\beta}_{3}^{2}+{\it\beta}_{4}^{2}\neq 0$, and 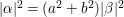 $|{\it\alpha}|^{2}=(a^{2}+b^{2})|{\it\beta}|^{2}$ and
$|{\it\alpha}|^{2}=(a^{2}+b^{2})|{\it\beta}|^{2}$ and ![]() $p^{2}$ does not divide
$p^{2}$ does not divide ![]() $|{\it\alpha}|^{2}$.
$|{\it\alpha}|^{2}$.
In [Reference Pitale23, page 69], it is shown that the set  $S_{1}=\{{\it\alpha}\in C_{p}:{\it\alpha}_{3}^{2}+{\it\alpha}_{4}^{2}\not \equiv 0~(\text{mod}~p)\}$ is in bijection with the set
$S_{1}=\{{\it\alpha}\in C_{p}:{\it\alpha}_{3}^{2}+{\it\alpha}_{4}^{2}\not \equiv 0~(\text{mod}~p)\}$ is in bijection with the set  $S_{2}=\{(x,y)\in \mathbb{Z}_{p}\times \mathbb{Z}_{p}:x^{2}+y^{2}+1\equiv 0~(\text{mod}~p)\}$. The map from
$S_{2}=\{(x,y)\in \mathbb{Z}_{p}\times \mathbb{Z}_{p}:x^{2}+y^{2}+1\equiv 0~(\text{mod}~p)\}$. The map from ![]() $S_{1}$ to
$S_{1}$ to ![]() $S_{2}$ is given as follows. For
$S_{2}$ is given as follows. For ![]() ${\it\alpha}\in S_{1}$, we obtain
${\it\alpha}\in S_{1}$, we obtain  $(x_{{\it\alpha}},y_{{\it\alpha}})$ as the solution to the matrix equation modulo
$(x_{{\it\alpha}},y_{{\it\alpha}})$ as the solution to the matrix equation modulo ![]() $p$ given by
$p$ given by
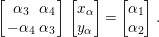 $$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}{\it\alpha}_{3} & {\it\alpha}_{4}\\ -{\it\alpha}_{4} & {\it\alpha}_{3}\end{array}\right]\left[\begin{array}{@{}c@{}}x_{{\it\alpha}}\\ y_{{\it\alpha}}\end{array}\right]=\left[\begin{array}{@{}c@{}}{\it\alpha}_{1}\\ {\it\alpha}_{2}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}{\it\alpha}_{3} & {\it\alpha}_{4}\\ -{\it\alpha}_{4} & {\it\alpha}_{3}\end{array}\right]\left[\begin{array}{@{}c@{}}x_{{\it\alpha}}\\ y_{{\it\alpha}}\end{array}\right]=\left[\begin{array}{@{}c@{}}{\it\alpha}_{1}\\ {\it\alpha}_{2}\end{array}\right].\end{eqnarray}$$ One can check that 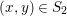 $(x,y)\in S_{2}$ for the following choice of
$(x,y)\in S_{2}$ for the following choice of ![]() $x$ and
$x$ and ![]() $y$:
$y$:
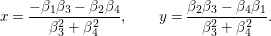 $$\begin{eqnarray}x=\frac{-{\it\beta}_{1}{\it\beta}_{3}-{\it\beta}_{2}{\it\beta}_{4}}{{\it\beta}_{3}^{2}+{\it\beta}_{4}^{2}},\qquad y=\frac{{\it\beta}_{2}{\it\beta}_{3}-{\it\beta}_{4}{\it\beta}_{1}}{{\it\beta}_{3}^{2}+{\it\beta}_{4}^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}x=\frac{-{\it\beta}_{1}{\it\beta}_{3}-{\it\beta}_{2}{\it\beta}_{4}}{{\it\beta}_{3}^{2}+{\it\beta}_{4}^{2}},\qquad y=\frac{{\it\beta}_{2}{\it\beta}_{3}-{\it\beta}_{4}{\it\beta}_{1}}{{\it\beta}_{3}^{2}+{\it\beta}_{4}^{2}}.\end{eqnarray}$$ If we take ![]() ${\it\alpha}\in S_{1}$ to be the preimage of the above
${\it\alpha}\in S_{1}$ to be the preimage of the above ![]() $(x,y)$, then we can check that
$(x,y)$, then we can check that 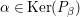 ${\it\alpha}\in \text{Ker}(P_{{\it\beta}})$. On the other hand, if
${\it\alpha}\in \text{Ker}(P_{{\it\beta}})$. On the other hand, if ![]() ${\it\alpha}\in C_{p}$ belongs to
${\it\alpha}\in C_{p}$ belongs to 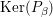 $\text{Ker}(P_{{\it\beta}})$, then it can also be checked that the corresponding
$\text{Ker}(P_{{\it\beta}})$, then it can also be checked that the corresponding 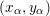 $(x_{{\it\alpha}},y_{{\it\alpha}})$ are equivalent modulo
$(x_{{\it\alpha}},y_{{\it\alpha}})$ are equivalent modulo ![]() $p$ to those in (5.10). This completes the proof of (5.9).
$p$ to those in (5.10). This completes the proof of (5.9).
If ![]() $p^{2}$ divides
$p^{2}$ divides ![]() ${\it\beta}{\it\alpha}$ or
${\it\beta}{\it\alpha}$ or ![]() ${\it\alpha}{\it\beta}$ for some
${\it\alpha}{\it\beta}$ for some ![]() ${\it\alpha}\in C_{p}$, then it is clear that
${\it\alpha}\in C_{p}$, then it is clear that ![]() ${\it\beta}$ cannot be primitive. This completes the proof of the lemma.◻
${\it\beta}$ cannot be primitive. This completes the proof of the lemma.◻
Proposition 5.11. Let 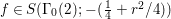 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue ![]() ${\it\lambda}_{p}$ for every odd prime
${\it\lambda}_{p}$ for every odd prime ![]() $p$. Let
$p$. Let ![]() $F=F_{f}$ be as defined in Theorem 4.4. For an odd prime
$F=F_{f}$ be as defined in Theorem 4.4. For an odd prime ![]() $p$ we then have
$p$ we then have
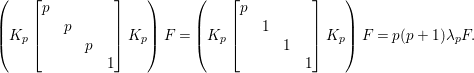 $$\begin{eqnarray}\displaystyle \left(K_{p}\left[\begin{array}{@{}cccc@{}}p\\ & p\\ & & p\\ & & & 1\end{array}\right]K_{p}\right)F=\left(K_{p}\left[\begin{array}{@{}cccc@{}}p\\ & 1\\ & & 1\\ & & & 1\end{array}\right]K_{p}\right)F=p(p+1){\it\lambda}_{p}F. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(K_{p}\left[\begin{array}{@{}cccc@{}}p\\ & p\\ & & p\\ & & & 1\end{array}\right]K_{p}\right)F=\left(K_{p}\left[\begin{array}{@{}cccc@{}}p\\ & 1\\ & & 1\\ & & & 1\end{array}\right]K_{p}\right)F=p(p+1){\it\lambda}_{p}F. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$Proof. Using Proposition 5.8 we can show that, if the Fourier coefficients satisfy 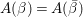 $A({\it\beta})=A(\bar{{\it\beta}})$ for all
$A({\it\beta})=A(\bar{{\it\beta}})$ for all ![]() ${\it\beta}\in S$ and the second equality in (5.11) holds, then so does the first equality. Since the Fourier coefficients of
${\it\beta}\in S$ and the second equality in (5.11) holds, then so does the first equality. Since the Fourier coefficients of ![]() $F=F_{f}$ satisfy the above condition, we are reduced to showing the second equality in (5.11).
$F=F_{f}$ satisfy the above condition, we are reduced to showing the second equality in (5.11).
We will compute the action of the Hecke operator on the Fourier coefficients ![]() $A({\it\beta})$ of
$A({\it\beta})$ of ![]() $F$. Since all the computations only involve the prime
$F$. Since all the computations only involve the prime ![]() $p$, it will be enough to consider the case
$p$, it will be enough to consider the case 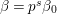 ${\it\beta}=p^{s}{\it\beta}_{0}$ with
${\it\beta}=p^{s}{\it\beta}_{0}$ with ![]() $s\geqslant 0$ and
$s\geqslant 0$ and 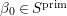 ${\it\beta}_{0}\in S^{\text{prim}}$. For such a
${\it\beta}_{0}\in S^{\text{prim}}$. For such a ![]() ${\it\beta}$, we have
${\it\beta}$, we have
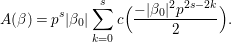 $$\begin{eqnarray}A({\it\beta})=p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big).\end{eqnarray}$$
$$\begin{eqnarray}A({\it\beta})=p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big).\end{eqnarray}$$ Note that 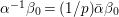 ${\it\alpha}^{-1}{\it\beta}_{0}=(1/p)\bar{{\it\alpha}}{\it\beta}_{0}$ for
${\it\alpha}^{-1}{\it\beta}_{0}=(1/p)\bar{{\it\alpha}}{\it\beta}_{0}$ for ![]() ${\it\alpha}\in B$ with
${\it\alpha}\in B$ with 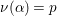 ${\it\nu}({\it\alpha})=p$. Hence, for such
${\it\nu}({\it\alpha})=p$. Hence, for such ![]() ${\it\alpha}$,
${\it\alpha}$, 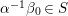 ${\it\alpha}^{-1}{\it\beta}_{0}\in S$ if and only if
${\it\alpha}^{-1}{\it\beta}_{0}\in S$ if and only if ![]() $p$ divides
$p$ divides ![]() $\bar{{\it\alpha}}{\it\beta}_{0}$.
$\bar{{\it\alpha}}{\it\beta}_{0}$.
Let us first consider the case where ![]() $p$ does not divide
$p$ does not divide ![]() $|{\it\beta}_{0}|^{2}$. Hence, by Lemma 5.10, we see that
$|{\it\beta}_{0}|^{2}$. Hence, by Lemma 5.10, we see that 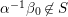 ${\it\alpha}^{-1}{\it\beta}_{0}\not \in S$ and
${\it\alpha}^{-1}{\it\beta}_{0}\not \in S$ and ![]() $p$ does not divide
$p$ does not divide ![]() ${\it\beta}_{0}{\it\alpha}$ for any
${\it\beta}_{0}{\it\alpha}$ for any ![]() ${\it\alpha}\in C_{p}$. Hence, for any
${\it\alpha}\in C_{p}$. Hence, for any ![]() ${\it\alpha}\in C_{p}$, we have
${\it\alpha}\in C_{p}$, we have
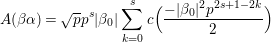 $$\begin{eqnarray}A({\it\beta}{\it\alpha})=\sqrt{p}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s+1-2k}}{2}\Big)\end{eqnarray}$$
$$\begin{eqnarray}A({\it\beta}{\it\alpha})=\sqrt{p}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s+1-2k}}{2}\Big)\end{eqnarray}$$and
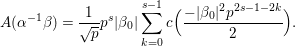 $$\begin{eqnarray}A({\it\alpha}^{-1}{\it\beta})=\frac{1}{\sqrt{p}}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-1-2k}}{2}\Big).\end{eqnarray}$$
$$\begin{eqnarray}A({\it\alpha}^{-1}{\it\beta})=\frac{1}{\sqrt{p}}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-1-2k}}{2}\Big).\end{eqnarray}$$ Note that, if ![]() $s=0$, both the left- and right-hand sides of the last equation are zero. Now, using (5.8), we get for any
$s=0$, both the left- and right-hand sides of the last equation are zero. Now, using (5.8), we get for any ![]() ${\it\alpha}\in C_{p}$
${\it\alpha}\in C_{p}$
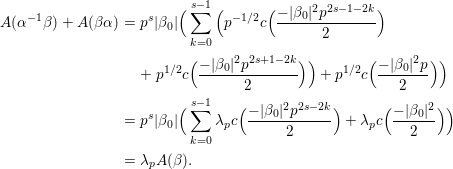 $$\begin{eqnarray}\displaystyle A({\it\alpha}^{-1}{\it\beta})+A({\it\beta}{\it\alpha}) & = & \displaystyle p^{s}|{\it\beta}_{0}|\Big(\mathop{\sum }_{k=0}^{s-1}\Big(p^{-1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-1-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle +\,p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s+1-2k}}{2}\Big)\Big)+p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p}{2}\Big)\Big)\nonumber\\ \displaystyle & = & \displaystyle p^{s}|{\it\beta}_{0}|\Big(\mathop{\sum }_{k=0}^{s-1}{\it\lambda}_{p}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+{\it\lambda}_{p}c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & = & \displaystyle {\it\lambda}_{p}A({\it\beta}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A({\it\alpha}^{-1}{\it\beta})+A({\it\beta}{\it\alpha}) & = & \displaystyle p^{s}|{\it\beta}_{0}|\Big(\mathop{\sum }_{k=0}^{s-1}\Big(p^{-1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-1-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle +\,p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s+1-2k}}{2}\Big)\Big)+p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p}{2}\Big)\Big)\nonumber\\ \displaystyle & = & \displaystyle p^{s}|{\it\beta}_{0}|\Big(\mathop{\sum }_{k=0}^{s-1}{\it\lambda}_{p}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+{\it\lambda}_{p}c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & = & \displaystyle {\it\lambda}_{p}A({\it\beta}).\nonumber\end{eqnarray}$$ Now, using the fact that the number of elements in ![]() $C_{p}$ is
$C_{p}$ is ![]() $p+1$ and part (2b) of Proposition 5.8, we get the result.
$p+1$ and part (2b) of Proposition 5.8, we get the result.
Next, let us assume that ![]() $p$ divides
$p$ divides ![]() $|{\it\beta}_{0}|^{2}$. By Lemma 5.10, there is a unique
$|{\it\beta}_{0}|^{2}$. By Lemma 5.10, there is a unique 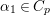 ${\it\alpha}_{1}\in C_{p}$ such that
${\it\alpha}_{1}\in C_{p}$ such that ![]() $p$ divides
$p$ divides ![]() ${\it\beta}_{0}{\it\alpha}_{1}$, and a unique
${\it\beta}_{0}{\it\alpha}_{1}$, and a unique 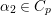 ${\it\alpha}_{2}\in C_{p}$ such that
${\it\alpha}_{2}\in C_{p}$ such that 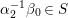 ${\it\alpha}_{2}^{-1}{\it\beta}_{0}\in S$. If
${\it\alpha}_{2}^{-1}{\it\beta}_{0}\in S$. If ![]() ${\it\alpha}\in C_{p}$ but
${\it\alpha}\in C_{p}$ but ![]() ${\it\alpha}\neq {\it\alpha}_{1}$, then the formula for
${\it\alpha}\neq {\it\alpha}_{1}$, then the formula for ![]() $A({\it\beta}{\it\alpha})$ is the same as in (5.12). For
$A({\it\beta}{\it\alpha})$ is the same as in (5.12). For ![]() ${\it\alpha}={\it\alpha}_{1}$, we have
${\it\alpha}={\it\alpha}_{1}$, we have
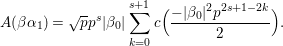 $$\begin{eqnarray}A({\it\beta}{\it\alpha}_{1})=\sqrt{p}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s+1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s+1-2k}}{2}\Big).\end{eqnarray}$$
$$\begin{eqnarray}A({\it\beta}{\it\alpha}_{1})=\sqrt{p}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s+1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s+1-2k}}{2}\Big).\end{eqnarray}$$ For ![]() ${\it\alpha}\in C_{p}$ but
${\it\alpha}\in C_{p}$ but ![]() ${\it\alpha}\neq {\it\alpha}_{2}$, the formula for
${\it\alpha}\neq {\it\alpha}_{2}$, the formula for 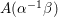 $A({\it\alpha}^{-1}{\it\beta})$ is the same as in (5.13). For
$A({\it\alpha}^{-1}{\it\beta})$ is the same as in (5.13). For ![]() ${\it\alpha}={\it\alpha}_{2}$, we have
${\it\alpha}={\it\alpha}_{2}$, we have
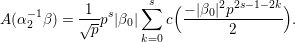 $$\begin{eqnarray}A({\it\alpha}_{2}^{-1}{\it\beta})=\frac{1}{\sqrt{p}}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-1-2k}}{2}\Big).\end{eqnarray}$$
$$\begin{eqnarray}A({\it\alpha}_{2}^{-1}{\it\beta})=\frac{1}{\sqrt{p}}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-1-2k}}{2}\Big).\end{eqnarray}$$Hence, we get the following:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{{\it\alpha}\in C_{p}}(A({\it\alpha}^{-1}{\it\beta})+A({\it\beta}{\it\alpha}))\nonumber\\ \displaystyle & & \displaystyle \quad =pp^{s}|{\it\beta}_{0}|\Big[\mathop{\sum }_{k=0}^{s}p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s+1-2k}}{2}\Big)+\mathop{\sum }_{k=0}^{s-1}p^{-1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-1-2k}}{2}\Big)\Big]\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,p^{s}|{\it\beta}_{0}|\Big[\mathop{\sum }_{k=0}^{s+1}p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s+1-2k}}{2}\Big)+\mathop{\sum }_{k=0}^{s}p^{-1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-1-2k}}{2}\Big)\Big]\nonumber\\ \displaystyle & & \displaystyle \quad =pp^{s}|{\it\beta}_{0}|\Big[\mathop{\sum }_{k=0}^{s-1}{\it\lambda}_{p}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p}{2}\Big)\Big]\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,p^{s}|{\it\beta}_{0}|\Big[\mathop{\sum }_{k=0}^{s}{\it\lambda}_{p}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2p}\Big)\Big]\nonumber\\ \displaystyle & & \displaystyle \quad ={\it\lambda}_{p}A({\it\beta})+pp^{s}|{\it\beta}_{0}|\Big[\mathop{\sum }_{k=0}^{s-1}{\it\lambda}_{p}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p}{2}\Big)+p^{-1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2p}\Big)\Big]\nonumber\\ \displaystyle & & \displaystyle \quad ={\it\lambda}_{p}A({\it\beta})+p{\it\lambda}_{p}A({\it\beta})=(p+1){\it\lambda}_{p}A({\it\beta}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{{\it\alpha}\in C_{p}}(A({\it\alpha}^{-1}{\it\beta})+A({\it\beta}{\it\alpha}))\nonumber\\ \displaystyle & & \displaystyle \quad =pp^{s}|{\it\beta}_{0}|\Big[\mathop{\sum }_{k=0}^{s}p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s+1-2k}}{2}\Big)+\mathop{\sum }_{k=0}^{s-1}p^{-1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-1-2k}}{2}\Big)\Big]\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,p^{s}|{\it\beta}_{0}|\Big[\mathop{\sum }_{k=0}^{s+1}p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s+1-2k}}{2}\Big)+\mathop{\sum }_{k=0}^{s}p^{-1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-1-2k}}{2}\Big)\Big]\nonumber\\ \displaystyle & & \displaystyle \quad =pp^{s}|{\it\beta}_{0}|\Big[\mathop{\sum }_{k=0}^{s-1}{\it\lambda}_{p}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p}{2}\Big)\Big]\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,p^{s}|{\it\beta}_{0}|\Big[\mathop{\sum }_{k=0}^{s}{\it\lambda}_{p}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2p}\Big)\Big]\nonumber\\ \displaystyle & & \displaystyle \quad ={\it\lambda}_{p}A({\it\beta})+pp^{s}|{\it\beta}_{0}|\Big[\mathop{\sum }_{k=0}^{s-1}{\it\lambda}_{p}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,p^{1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}p}{2}\Big)+p^{-1/2}c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2p}\Big)\Big]\nonumber\\ \displaystyle & & \displaystyle \quad ={\it\lambda}_{p}A({\it\beta})+p{\it\lambda}_{p}A({\it\beta})=(p+1){\it\lambda}_{p}A({\it\beta}).\nonumber\end{eqnarray}$$This completes the proof of the proposition. ◻
Proposition 5.12. Let 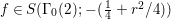 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue ![]() ${\it\lambda}_{p}$ for every odd prime
${\it\lambda}_{p}$ for every odd prime ![]() $p$. Let
$p$. Let ![]() $F=F_{f}$ be as defined in Theorem 4.4. For an odd prime
$F=F_{f}$ be as defined in Theorem 4.4. For an odd prime ![]() $p$ we then have
$p$ we then have
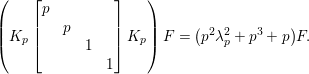 $$\begin{eqnarray}\left(K_{p}\left[\begin{array}{@{}cccc@{}}p\\ & p\\ & & 1\\ & & & 1\end{array}\right]K_{p}\right)F=\big(p^{2}{\it\lambda}_{p}^{2}+p^{3}+p\big)F.\end{eqnarray}$$
$$\begin{eqnarray}\left(K_{p}\left[\begin{array}{@{}cccc@{}}p\\ & p\\ & & 1\\ & & & 1\end{array}\right]K_{p}\right)F=\big(p^{2}{\it\lambda}_{p}^{2}+p^{3}+p\big)F.\end{eqnarray}$$Proof. First observe that, using (5.8), one can show that, for all ![]() $n$,
$n$,
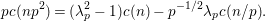 $$\begin{eqnarray}pc(np^{2})=({\it\lambda}_{p}^{2}-1)c(n)-p^{-1/2}{\it\lambda}_{p}c(n/p).\end{eqnarray}$$
$$\begin{eqnarray}pc(np^{2})=({\it\lambda}_{p}^{2}-1)c(n)-p^{-1/2}{\it\lambda}_{p}c(n/p).\end{eqnarray}$$ If we assume that ![]() $p|n$, then we can get another identity given by
$p|n$, then we can get another identity given by
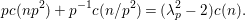 $$\begin{eqnarray}pc(np^{2})+p^{-1}c(n/p^{2})=({\it\lambda}_{p}^{2}-2)c(n).\end{eqnarray}$$
$$\begin{eqnarray}pc(np^{2})+p^{-1}c(n/p^{2})=({\it\lambda}_{p}^{2}-2)c(n).\end{eqnarray}$$ As in the proof of Proposition 5.11, we can assume that 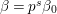 ${\it\beta}=p^{s}{\it\beta}_{0}$, where
${\it\beta}=p^{s}{\it\beta}_{0}$, where ![]() $s\geqslant 0$ and
$s\geqslant 0$ and 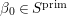 ${\it\beta}_{0}\in S^{\text{prim}}$. Let us abbreviate
${\it\beta}_{0}\in S^{\text{prim}}$. Let us abbreviate 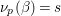 ${\it\nu}_{p}({\it\beta})=s$. For such a
${\it\nu}_{p}({\it\beta})=s$. For such a ![]() ${\it\beta}$ we have
${\it\beta}$ we have
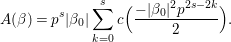 $$\begin{eqnarray}A({\it\beta})=p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big).\end{eqnarray}$$
$$\begin{eqnarray}A({\it\beta})=p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big).\end{eqnarray}$$Hence,
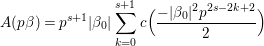 $$\begin{eqnarray}A(p{\it\beta})=p^{s+1}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s+1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k+2}}{2}\Big)\end{eqnarray}$$
$$\begin{eqnarray}A(p{\it\beta})=p^{s+1}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s+1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k+2}}{2}\Big)\end{eqnarray}$$and
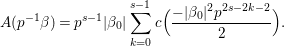 $$\begin{eqnarray}A(p^{-1}{\it\beta})=p^{s-1}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k-2}}{2}\Big).\end{eqnarray}$$
$$\begin{eqnarray}A(p^{-1}{\it\beta})=p^{s-1}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k-2}}{2}\Big).\end{eqnarray}$$ Next, we need to compute 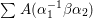 $\sum A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})$ where the sum is over all
$\sum A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})$ where the sum is over all ![]() ${\it\alpha}_{1},{\it\alpha}_{2}$ in
${\it\alpha}_{1},{\it\alpha}_{2}$ in ![]() $C_{p}$. We consider three cases depending on whether
$C_{p}$. We consider three cases depending on whether 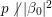 $p\not |\,|{\it\beta}_{0}|^{2}$, or
$p\not |\,|{\it\beta}_{0}|^{2}$, or ![]() $p|\,|{\it\beta}_{0}|^{2}$ but
$p|\,|{\it\beta}_{0}|^{2}$ but 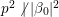 $p^{2}\not |\,|{\it\beta}_{0}|^{2}$ or
$p^{2}\not |\,|{\it\beta}_{0}|^{2}$ or 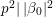 $p^{2}|\,|{\it\beta}_{0}|^{2}$.
$p^{2}|\,|{\it\beta}_{0}|^{2}$.
Case 1: Let us assume that 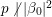 $p\not |\,|{\it\beta}_{0}|^{2}$. Applying Lemma 5.10 to
$p\not |\,|{\it\beta}_{0}|^{2}$. Applying Lemma 5.10 to ![]() ${\it\beta}_{0}$, we see that
${\it\beta}_{0}$, we see that 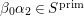 ${\it\beta}_{0}{\it\alpha}_{2}\in S^{\text{prim}}$ for all
${\it\beta}_{0}{\it\alpha}_{2}\in S^{\text{prim}}$ for all 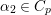 ${\it\alpha}_{2}\in C_{p}$. Again applying Lemma 5.10 to
${\it\alpha}_{2}\in C_{p}$. Again applying Lemma 5.10 to ![]() ${\it\beta}_{0}{\it\alpha}_{2}$ for a fixed
${\it\beta}_{0}{\it\alpha}_{2}$ for a fixed ![]() ${\it\alpha}_{2}$, we see there is a unique
${\it\alpha}_{2}$, we see there is a unique 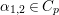 ${\it\alpha}_{1,2}\in C_{p}$ such that
${\it\alpha}_{1,2}\in C_{p}$ such that 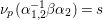 ${\it\nu}_{p}({\it\alpha}_{1,2}^{-1}{\it\beta}{\it\alpha}_{2})=s$, and, for all
${\it\nu}_{p}({\it\alpha}_{1,2}^{-1}{\it\beta}{\it\alpha}_{2})=s$, and, for all 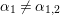 ${\it\alpha}_{1}\neq {\it\alpha}_{1,2}$, we have
${\it\alpha}_{1}\neq {\it\alpha}_{1,2}$, we have 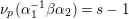 ${\it\nu}_{p}({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})=s-1$. Hence,
${\it\nu}_{p}({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})=s-1$. Hence,
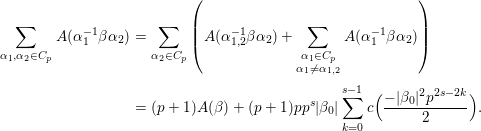 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{{\it\alpha}_{1},{\it\alpha}_{2}\in C_{p}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2}) & = & \displaystyle \mathop{\sum }_{{\it\alpha}_{2}\in C_{p}}\left(A({\it\alpha}_{1,2}^{-1}{\it\beta}{\it\alpha}_{2})+\mathop{\sum }_{\substack{ {\it\alpha}_{1}\in C_{p} \\ {\it\alpha}_{1}\neq {\it\alpha}_{1,2}}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})\right)\nonumber\\ \displaystyle & = & \displaystyle (p+1)A({\it\beta})+(p+1)pp^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{{\it\alpha}_{1},{\it\alpha}_{2}\in C_{p}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2}) & = & \displaystyle \mathop{\sum }_{{\it\alpha}_{2}\in C_{p}}\left(A({\it\alpha}_{1,2}^{-1}{\it\beta}{\it\alpha}_{2})+\mathop{\sum }_{\substack{ {\it\alpha}_{1}\in C_{p} \\ {\it\alpha}_{1}\neq {\it\alpha}_{1,2}}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})\right)\nonumber\\ \displaystyle & = & \displaystyle (p+1)A({\it\beta})+(p+1)pp^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big).\nonumber\end{eqnarray}$$ Putting this all together, we see that 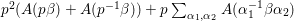 $p^{2}(A(p{\it\beta})+A(p^{-1}{\it\beta}))+p\sum _{{\it\alpha}_{1},{\it\alpha}_{2}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})$ is equal to
$p^{2}(A(p{\it\beta})+A(p^{-1}{\it\beta}))+p\sum _{{\it\alpha}_{1},{\it\alpha}_{2}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})$ is equal to
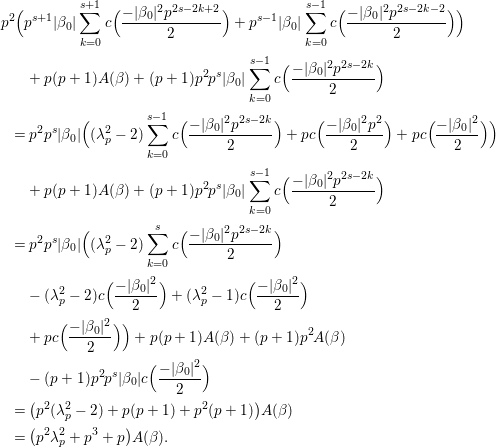 $$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-5.0pt}p^{2}\Big(p^{s+1}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s+1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k+2}}{2}\Big)+p^{s-1}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k-2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\qquad +\,p(p+1)A({\it\beta})+(p+1)p^{2}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\quad =p^{2}p^{s}|{\it\beta}_{0}|\Big(({\it\lambda}_{p}^{2}-2)\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\qquad +\,p(p+1)A({\it\beta})+(p+1)p^{2}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\quad =p^{2}p^{s}|{\it\beta}_{0}|\Big(({\it\lambda}_{p}^{2}-2)\mathop{\sum }_{k=0}^{s}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\qquad -\,({\it\lambda}_{p}^{2}-2)c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)+({\it\lambda}_{p}^{2}-1)c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\qquad +\,pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)+p(p+1)A({\it\beta})+(p+1)p^{2}A({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\qquad -\,(p+1)p^{2}p^{s}|{\it\beta}_{0}|c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\quad =\big(p^{2}({\it\lambda}_{p}^{2}-2)+p(p+1)+p^{2}(p+1)\big)A({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\quad =\big(p^{2}{\it\lambda}_{p}^{2}+p^{3}+p\big)A({\it\beta}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-5.0pt}p^{2}\Big(p^{s+1}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s+1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k+2}}{2}\Big)+p^{s-1}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k-2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\qquad +\,p(p+1)A({\it\beta})+(p+1)p^{2}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\quad =p^{2}p^{s}|{\it\beta}_{0}|\Big(({\it\lambda}_{p}^{2}-2)\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\qquad +\,p(p+1)A({\it\beta})+(p+1)p^{2}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\quad =p^{2}p^{s}|{\it\beta}_{0}|\Big(({\it\lambda}_{p}^{2}-2)\mathop{\sum }_{k=0}^{s}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\qquad -\,({\it\lambda}_{p}^{2}-2)c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)+({\it\lambda}_{p}^{2}-1)c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\qquad +\,pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)+p(p+1)A({\it\beta})+(p+1)p^{2}A({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\qquad -\,(p+1)p^{2}p^{s}|{\it\beta}_{0}|c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\quad =\big(p^{2}({\it\lambda}_{p}^{2}-2)+p(p+1)+p^{2}(p+1)\big)A({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \hspace{-6.00006pt}\quad =\big(p^{2}{\it\lambda}_{p}^{2}+p^{3}+p\big)A({\it\beta}).\nonumber\end{eqnarray}$$Here, we have used both (5.15) and (5.16).
Case 2: Let ![]() $p|\,|{\it\beta}_{0}|^{2}$ but
$p|\,|{\it\beta}_{0}|^{2}$ but 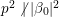 $p^{2}\not |\,|{\it\beta}_{0}|^{2}$. Applying Lemma 5.10 to
$p^{2}\not |\,|{\it\beta}_{0}|^{2}$. Applying Lemma 5.10 to ![]() ${\it\beta}_{0}$, we see that there is a unique
${\it\beta}_{0}$, we see that there is a unique  $\hat{{\it\alpha}}_{2}\in C_{p}$ such that
$\hat{{\it\alpha}}_{2}\in C_{p}$ such that ![]() $p|{\it\beta}_{0}\hat{{\it\alpha}}_{2}$. For
$p|{\it\beta}_{0}\hat{{\it\alpha}}_{2}$. For  ${\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}$, we have
${\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}$, we have 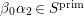 ${\it\beta}_{0}{\it\alpha}_{2}\in S^{\text{prim}}$. Let
${\it\beta}_{0}{\it\alpha}_{2}\in S^{\text{prim}}$. Let 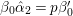 ${\it\beta}_{0}\hat{{\it\alpha}}_{2}=p{\it\beta}_{0}^{\prime }$. Then
${\it\beta}_{0}\hat{{\it\alpha}}_{2}=p{\it\beta}_{0}^{\prime }$. Then 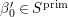 ${\it\beta}_{0}^{\prime }\in S^{\text{prim}}$ and
${\it\beta}_{0}^{\prime }\in S^{\text{prim}}$ and 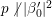 $p\not |\,|{\it\beta}_{0}^{\prime }|^{2}$ (since we have assumed that
$p\not |\,|{\it\beta}_{0}^{\prime }|^{2}$ (since we have assumed that 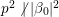 $p^{2}\not |\,|{\it\beta}_{0}|^{2}$). Hence, by Lemma 5.10, we see that, for all
$p^{2}\not |\,|{\it\beta}_{0}|^{2}$). Hence, by Lemma 5.10, we see that, for all 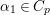 ${\it\alpha}_{1}\in C_{p}$, we have
${\it\alpha}_{1}\in C_{p}$, we have 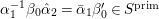 ${\it\alpha}_{1}^{-1}{\it\beta}_{0}\hat{{\it\alpha}}_{2}=\bar{{\it\alpha}}_{1}{\it\beta}_{0}^{\prime }\in S^{\text{prim}}$. This implies that
${\it\alpha}_{1}^{-1}{\it\beta}_{0}\hat{{\it\alpha}}_{2}=\bar{{\it\alpha}}_{1}{\it\beta}_{0}^{\prime }\in S^{\text{prim}}$. This implies that 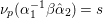 ${\it\nu}_{p}({\it\alpha}_{1}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})=s$ for all
${\it\nu}_{p}({\it\alpha}_{1}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})=s$ for all 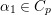 ${\it\alpha}_{1}\in C_{p}$. If
${\it\alpha}_{1}\in C_{p}$. If 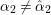 ${\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}$, then Lemma 5.10 implies that there is a unique
${\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}$, then Lemma 5.10 implies that there is a unique 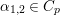 ${\it\alpha}_{1,2}\in C_{p}$ such that
${\it\alpha}_{1,2}\in C_{p}$ such that 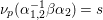 ${\it\nu}_{p}({\it\alpha}_{1,2}^{-1}{\it\beta}{\it\alpha}_{2})=s$. For all
${\it\nu}_{p}({\it\alpha}_{1,2}^{-1}{\it\beta}{\it\alpha}_{2})=s$. For all 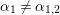 ${\it\alpha}_{1}\neq {\it\alpha}_{1,2}$, we have
${\it\alpha}_{1}\neq {\it\alpha}_{1,2}$, we have 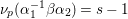 ${\it\nu}_{p}({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})=s-1$. This gives us
${\it\nu}_{p}({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})=s-1$. This gives us
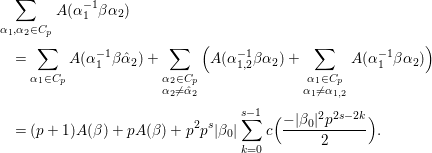 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{{\it\alpha}_{1},{\it\alpha}_{2}\in C_{p}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{{\it\alpha}_{1}\in C_{p}}A({\it\alpha}_{1}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})+\mathop{\sum }_{\substack{ {\it\alpha}_{2}\in C_{p} \\ {\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}}}\Big(A({\it\alpha}_{1,2}^{-1}{\it\beta}{\it\alpha}_{2})+\mathop{\sum }_{\substack{ {\it\alpha}_{1}\in C_{p} \\ {\it\alpha}_{1}\neq {\it\alpha}_{1,2}}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =(p+1)A({\it\beta})+pA({\it\beta})+p^{2}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{{\it\alpha}_{1},{\it\alpha}_{2}\in C_{p}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{{\it\alpha}_{1}\in C_{p}}A({\it\alpha}_{1}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})+\mathop{\sum }_{\substack{ {\it\alpha}_{2}\in C_{p} \\ {\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}}}\Big(A({\it\alpha}_{1,2}^{-1}{\it\beta}{\it\alpha}_{2})+\mathop{\sum }_{\substack{ {\it\alpha}_{1}\in C_{p} \\ {\it\alpha}_{1}\neq {\it\alpha}_{1,2}}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =(p+1)A({\it\beta})+pA({\it\beta})+p^{2}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big).\nonumber\end{eqnarray}$$ Putting this all together, we see that 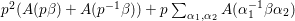 $p^{2}(A(p{\it\beta})+A(p^{-1}{\it\beta}))+p\sum _{{\it\alpha}_{1},{\it\alpha}_{2}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})$ is equal to
$p^{2}(A(p{\it\beta})+A(p^{-1}{\it\beta}))+p\sum _{{\it\alpha}_{1},{\it\alpha}_{2}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})$ is equal to
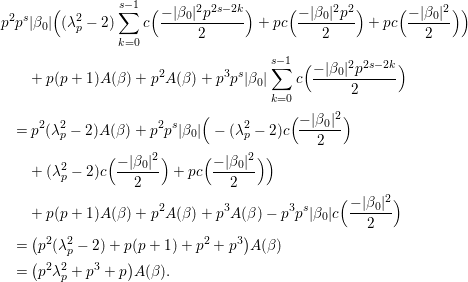 $$\begin{eqnarray}\displaystyle & & \displaystyle p^{2}p^{s}|{\it\beta}_{0}|\Big(({\it\lambda}_{p}^{2}-2)\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,p(p+1)A({\it\beta})+p^{2}A({\it\beta})+p^{3}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =p^{2}({\it\lambda}_{p}^{2}-2)A({\it\beta})+p^{2}p^{s}|{\it\beta}_{0}|\Big(-({\it\lambda}_{p}^{2}-2)c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,({\it\lambda}_{p}^{2}-2)c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,p(p+1)A({\it\beta})+p^{2}A({\it\beta})+p^{3}A({\it\beta})-p^{3}p^{s}|{\it\beta}_{0}|c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =\big(p^{2}({\it\lambda}_{p}^{2}-2)+p(p+1)+p^{2}+p^{3}\big)A({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \quad =\big(p^{2}{\it\lambda}_{p}^{2}+p^{3}+p\big)A({\it\beta}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle p^{2}p^{s}|{\it\beta}_{0}|\Big(({\it\lambda}_{p}^{2}-2)\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,p(p+1)A({\it\beta})+p^{2}A({\it\beta})+p^{3}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =p^{2}({\it\lambda}_{p}^{2}-2)A({\it\beta})+p^{2}p^{s}|{\it\beta}_{0}|\Big(-({\it\lambda}_{p}^{2}-2)c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,({\it\lambda}_{p}^{2}-2)c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,p(p+1)A({\it\beta})+p^{2}A({\it\beta})+p^{3}A({\it\beta})-p^{3}p^{s}|{\it\beta}_{0}|c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =\big(p^{2}({\it\lambda}_{p}^{2}-2)+p(p+1)+p^{2}+p^{3}\big)A({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \quad =\big(p^{2}{\it\lambda}_{p}^{2}+p^{3}+p\big)A({\it\beta}).\nonumber\end{eqnarray}$$ Here, we have used (5.16) and ![]() $p|\,|{\it\beta}_{0}|^{2}$.
$p|\,|{\it\beta}_{0}|^{2}$.
Case 3: Let 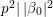 $p^{2}|\,|{\it\beta}_{0}|^{2}$. As in Case 2 above, Lemma 5.10 applied to
$p^{2}|\,|{\it\beta}_{0}|^{2}$. As in Case 2 above, Lemma 5.10 applied to ![]() ${\it\beta}_{0}$ implies that there is a unique
${\it\beta}_{0}$ implies that there is a unique 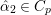 $\hat{{\it\alpha}}_{2}\in C_{p}$ such that
$\hat{{\it\alpha}}_{2}\in C_{p}$ such that ![]() $p|{\it\beta}_{0}\hat{{\it\alpha}}_{2}$. For
$p|{\it\beta}_{0}\hat{{\it\alpha}}_{2}$. For 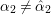 ${\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}$, we have
${\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}$, we have 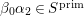 ${\it\beta}_{0}{\it\alpha}_{2}\in S^{\text{prim}}$. Let
${\it\beta}_{0}{\it\alpha}_{2}\in S^{\text{prim}}$. Let 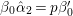 ${\it\beta}_{0}\hat{{\it\alpha}}_{2}=p{\it\beta}_{0}^{\prime }$. Then
${\it\beta}_{0}\hat{{\it\alpha}}_{2}=p{\it\beta}_{0}^{\prime }$. Then 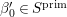 ${\it\beta}_{0}^{\prime }\in S^{\text{prim}}$ and
${\it\beta}_{0}^{\prime }\in S^{\text{prim}}$ and ![]() $p|\,|{\it\beta}_{0}^{\prime }|^{2}$ (since we have assumed
$p|\,|{\it\beta}_{0}^{\prime }|^{2}$ (since we have assumed 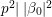 $p^{2}|\,|{\it\beta}_{0}|^{2}$). Hence, by Lemma 5.10, there is a unique
$p^{2}|\,|{\it\beta}_{0}|^{2}$). Hence, by Lemma 5.10, there is a unique 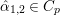 $\hat{{\it\alpha}}_{1,2}\in C_{p}$ such that
$\hat{{\it\alpha}}_{1,2}\in C_{p}$ such that 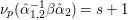 ${\it\nu}_{p}(\hat{{\it\alpha}}_{1,2}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})=s+1$, and for all
${\it\nu}_{p}(\hat{{\it\alpha}}_{1,2}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})=s+1$, and for all 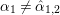 ${\it\alpha}_{1}\neq \hat{{\it\alpha}}_{1,2}$, we have
${\it\alpha}_{1}\neq \hat{{\it\alpha}}_{1,2}$, we have 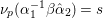 ${\it\nu}_{p}({\it\alpha}_{1}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})=s$. If
${\it\nu}_{p}({\it\alpha}_{1}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})=s$. If 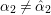 ${\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}$, then Lemma 5.10 implies that there is a unique
${\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}$, then Lemma 5.10 implies that there is a unique 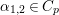 ${\it\alpha}_{1,2}\in C_{p}$ such that
${\it\alpha}_{1,2}\in C_{p}$ such that 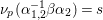 ${\it\nu}_{p}({\it\alpha}_{1,2}^{-1}{\it\beta}{\it\alpha}_{2})=s$. For all
${\it\nu}_{p}({\it\alpha}_{1,2}^{-1}{\it\beta}{\it\alpha}_{2})=s$. For all 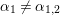 ${\it\alpha}_{1}\neq {\it\alpha}_{1,2}$, we have
${\it\alpha}_{1}\neq {\it\alpha}_{1,2}$, we have 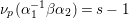 ${\it\nu}_{p}({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})=s-1$. This gives us that
${\it\nu}_{p}({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})=s-1$. This gives us that 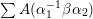 $\sum A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})$ is equal to
$\sum A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})$ is equal to
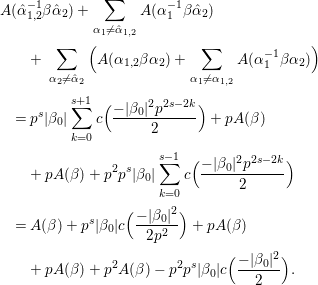 $$\begin{eqnarray}\displaystyle & & \displaystyle A(\hat{{\it\alpha}}_{1,2}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})+\mathop{\sum }_{{\it\alpha}_{1}\neq \hat{{\it\alpha}}_{1,2}}A({\it\alpha}_{1}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{{\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}}\Big(A({\it\alpha}_{1,2}{\it\beta}{\it\alpha}_{2})+\mathop{\sum }_{{\it\alpha}_{1}\neq {\it\alpha}_{1,2}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s+1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+pA({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,pA({\it\beta})+p^{2}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =A({\it\beta})+p^{s}|{\it\beta}_{0}|c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2p^{2}}\Big)+pA({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,pA({\it\beta})+p^{2}A({\it\beta})-p^{2}p^{s}|{\it\beta}_{0}|c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle A(\hat{{\it\alpha}}_{1,2}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})+\mathop{\sum }_{{\it\alpha}_{1}\neq \hat{{\it\alpha}}_{1,2}}A({\it\alpha}_{1}^{-1}{\it\beta}\hat{{\it\alpha}}_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{{\it\alpha}_{2}\neq \hat{{\it\alpha}}_{2}}\Big(A({\it\alpha}_{1,2}{\it\beta}{\it\alpha}_{2})+\mathop{\sum }_{{\it\alpha}_{1}\neq {\it\alpha}_{1,2}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s+1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)+pA({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,pA({\it\beta})+p^{2}p^{s}|{\it\beta}_{0}|\mathop{\sum }_{k=0}^{s-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2s-2k}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =A({\it\beta})+p^{s}|{\it\beta}_{0}|c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2p^{2}}\Big)+pA({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,pA({\it\beta})+p^{2}A({\it\beta})-p^{2}p^{s}|{\it\beta}_{0}|c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big).\nonumber\end{eqnarray}$$ Putting this all together, we see that 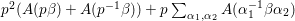 $p^{2}(A(p{\it\beta})+A(p^{-1}{\it\beta}))+p\sum _{{\it\alpha}_{1},{\it\alpha}_{2}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})$ is equal to
$p^{2}(A(p{\it\beta})+A(p^{-1}{\it\beta}))+p\sum _{{\it\alpha}_{1},{\it\alpha}_{2}}A({\it\alpha}_{1}^{-1}{\it\beta}{\it\alpha}_{2})$ is equal to
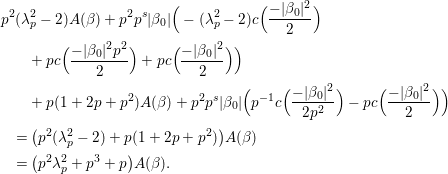 $$\begin{eqnarray}\displaystyle & & \displaystyle p^{2}({\it\lambda}_{p}^{2}-2)A({\it\beta})+p^{2}p^{s}|{\it\beta}_{0}|\Big(-({\it\lambda}_{p}^{2}-2)c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,pc\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,p(1+2p+p^{2})A({\it\beta})+p^{2}p^{s}|{\it\beta}_{0}|\Big(p^{-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2p^{2}}\Big)-pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =\big(p^{2}({\it\lambda}_{p}^{2}-2)+p(1+2p+p^{2})\big)A({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \quad =\big(p^{2}{\it\lambda}_{p}^{2}+p^{3}+p\big)A({\it\beta}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle p^{2}({\it\lambda}_{p}^{2}-2)A({\it\beta})+p^{2}p^{s}|{\it\beta}_{0}|\Big(-({\it\lambda}_{p}^{2}-2)c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,pc\Big(\frac{-|{\it\beta}_{0}|^{2}p^{2}}{2}\Big)+pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,p(1+2p+p^{2})A({\it\beta})+p^{2}p^{s}|{\it\beta}_{0}|\Big(p^{-1}c\Big(\frac{-|{\it\beta}_{0}|^{2}}{2p^{2}}\Big)-pc\Big(\frac{-|{\it\beta}_{0}|^{2}}{2}\Big)\Big)\nonumber\\ \displaystyle & & \displaystyle \quad =\big(p^{2}({\it\lambda}_{p}^{2}-2)+p(1+2p+p^{2})\big)A({\it\beta})\nonumber\\ \displaystyle & & \displaystyle \quad =\big(p^{2}{\it\lambda}_{p}^{2}+p^{3}+p\big)A({\it\beta}).\nonumber\end{eqnarray}$$ Here, we have used (5.16) and 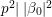 $p^{2}|\,|{\it\beta}_{0}|^{2}$. This completes the proof of the proposition.◻
$p^{2}|\,|{\it\beta}_{0}|^{2}$. This completes the proof of the proposition.◻
6 The automorphic representation corresponding to the lifting
In this section, we will use the Hecke equivariance from the previous section to determine the local components of the automorphic representation corresponding to the lifting. This will lead us to the conclusion that we have obtained a CAP representation and have found a counterexample to the Ramanujan conjecture.
6.1 The local components of the automorphic representation
Let 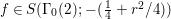 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue ![]() ${\it\lambda}_{p}$ for every odd prime
${\it\lambda}_{p}$ for every odd prime ![]() $p$. Let
$p$. Let ![]() $F=F_{f}$ be as defined in Theorem 4.4. Let
$F=F_{f}$ be as defined in Theorem 4.4. Let 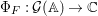 ${\rm\Phi}_{F}:{\mathcal{G}}(\mathbb{A})\rightarrow \mathbb{C}$ be defined by
${\rm\Phi}_{F}:{\mathcal{G}}(\mathbb{A})\rightarrow \mathbb{C}$ be defined by
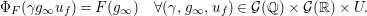 $$\begin{eqnarray}{\rm\Phi}_{F}({\it\gamma}g_{\infty }u_{f})=F(g_{\infty })\quad \forall ({\it\gamma},g_{\infty },u_{f})\in {\mathcal{G}}(\mathbb{Q})\times {\mathcal{G}}(\mathbb{R})\times U.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Phi}_{F}({\it\gamma}g_{\infty }u_{f})=F(g_{\infty })\quad \forall ({\it\gamma},g_{\infty },u_{f})\in {\mathcal{G}}(\mathbb{Q})\times {\mathcal{G}}(\mathbb{R})\times U.\end{eqnarray}$$ See Section 5.1 for details. Let ![]() ${\it\pi}_{F}$ be the irreducible cuspidal automorphic representation of
${\it\pi}_{F}$ be the irreducible cuspidal automorphic representation of ![]() ${\mathcal{G}}(\mathbb{A})$ generated by the right translates of
${\mathcal{G}}(\mathbb{A})$ generated by the right translates of ![]() ${\rm\Phi}_{F}$. Note that the irreducibility follows from the strong multiplicity-one result for
${\rm\Phi}_{F}$. Note that the irreducibility follows from the strong multiplicity-one result for ![]() ${\mathcal{G}}(\mathbb{A})$ (see [Reference Badulescu2], [Reference Badulescu and Renard3]). The representation
${\mathcal{G}}(\mathbb{A})$ (see [Reference Badulescu2], [Reference Badulescu and Renard3]). The representation ![]() ${\it\pi}_{F}$ is cuspidal since
${\it\pi}_{F}$ is cuspidal since ![]() $F$ is a cusp form. Let
$F$ is a cusp form. Let 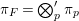 ${\it\pi}_{F}=\otimes _{p}^{\prime }{\it\pi}_{p}$, where
${\it\pi}_{F}=\otimes _{p}^{\prime }{\it\pi}_{p}$, where ![]() ${\it\pi}_{p}$ is an irreducible admissible representation of
${\it\pi}_{p}$ is an irreducible admissible representation of 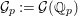 ${\mathcal{G}}_{p}:={\mathcal{G}}(\mathbb{Q}_{p})$ for
${\mathcal{G}}_{p}:={\mathcal{G}}(\mathbb{Q}_{p})$ for ![]() $p<\infty$, and
$p<\infty$, and ![]() ${\it\pi}_{\infty }$ is an irreducible admissible representation of
${\it\pi}_{\infty }$ is an irreducible admissible representation of ![]() ${\mathcal{G}}(\mathbb{R})$. Recall that
${\mathcal{G}}(\mathbb{R})$. Recall that 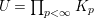 $U=\prod _{p<\infty }K_{p}$, where
$U=\prod _{p<\infty }K_{p}$, where ![]() $K_{p}$ is the maximal compact subgroup of
$K_{p}$ is the maximal compact subgroup of ![]() ${\mathcal{G}}(\mathbb{Q}_{p})$ (cf. Section 2.3). Hence, for
${\mathcal{G}}(\mathbb{Q}_{p})$ (cf. Section 2.3). Hence, for ![]() $p<\infty$, the representation
$p<\infty$, the representation ![]() ${\it\pi}_{p}$ is a spherical representation and can be realized as a subrepresentation of an unramified principal series representation, that is a representation induced from an unramified character of the Borel subgroup. The representation
${\it\pi}_{p}$ is a spherical representation and can be realized as a subrepresentation of an unramified principal series representation, that is a representation induced from an unramified character of the Borel subgroup. The representation ![]() ${\it\pi}_{p}$ is completely determined by the action of the Hecke algebra
${\it\pi}_{p}$ is completely determined by the action of the Hecke algebra 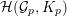 ${\mathcal{H}}({\mathcal{G}}_{p},K_{p})$ on the spherical vector in
${\mathcal{H}}({\mathcal{G}}_{p},K_{p})$ on the spherical vector in ![]() ${\it\pi}_{p}$, which, in turn, is completely determined by the Hecke eigenvalues of
${\it\pi}_{p}$, which, in turn, is completely determined by the Hecke eigenvalues of ![]() $F$ obtained in the previous section. See [Reference Cartier4] for details. For
$F$ obtained in the previous section. See [Reference Cartier4] for details. For ![]() $p=2$ we need to assume that
$p=2$ we need to assume that ![]() $f$ is a new form for the determination of the Hecke eigenvalue of
$f$ is a new form for the determination of the Hecke eigenvalue of ![]() $F_{f}$ (cf. Section 5.3).
$F_{f}$ (cf. Section 5.3).
Description of ![]() ${\it\pi}_{p}$for
${\it\pi}_{p}$for ![]() $p$odd
$p$odd
If ![]() $p$ is an odd prime, then we have
$p$ is an odd prime, then we have 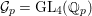 ${\mathcal{G}}_{p}=\text{GL}_{4}(\mathbb{Q}_{p})$ and
${\mathcal{G}}_{p}=\text{GL}_{4}(\mathbb{Q}_{p})$ and 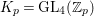 $K_{p}=\text{GL}_{4}(\mathbb{Z}_{p})$. Given
$K_{p}=\text{GL}_{4}(\mathbb{Z}_{p})$. Given ![]() $4$ unramified characters
$4$ unramified characters  ${\it\chi}_{1},{\it\chi}_{2},{\it\chi}_{3},{\it\chi}_{4}$ of
${\it\chi}_{1},{\it\chi}_{2},{\it\chi}_{3},{\it\chi}_{4}$ of ![]() $\mathbb{Q}_{p}^{\times }$, we obtain a character
$\mathbb{Q}_{p}^{\times }$, we obtain a character ![]() ${\it\chi}$ of the Borel subgroup
${\it\chi}$ of the Borel subgroup ![]() $P$ of upper triangular matrices in
$P$ of upper triangular matrices in ![]() ${\mathcal{G}}$, by
${\mathcal{G}}$, by
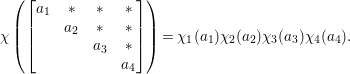 $$\begin{eqnarray}{\it\chi}\left(\left[\begin{array}{@{}cccc@{}}a_{1} & \ast & \ast & \ast \\ & a_{2} & \ast & \ast \\ & & a_{3} & \ast \\ & & & a_{4}\end{array}\right]\right)={\it\chi}_{1}(a_{1}){\it\chi}_{2}(a_{2}){\it\chi}_{3}(a_{3}){\it\chi}_{4}(a_{4}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\chi}\left(\left[\begin{array}{@{}cccc@{}}a_{1} & \ast & \ast & \ast \\ & a_{2} & \ast & \ast \\ & & a_{3} & \ast \\ & & & a_{4}\end{array}\right]\right)={\it\chi}_{1}(a_{1}){\it\chi}_{2}(a_{2}){\it\chi}_{3}(a_{3}){\it\chi}_{4}(a_{4}).\end{eqnarray}$$ The modulus character ![]() ${\it\delta}_{P}$ is given by
${\it\delta}_{P}$ is given by
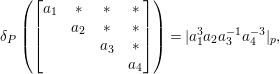 $$\begin{eqnarray}{\it\delta}_{P}\left(\left[\begin{array}{@{}cccc@{}}a_{1} & \ast & \ast & \ast \\ & a_{2} & \ast & \ast \\ & & a_{3} & \ast \\ & & & a_{4}\end{array}\right]\right)=|a_{1}^{3}a_{2}a_{3}^{-1}a_{4}^{-3}|_{p},\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}_{P}\left(\left[\begin{array}{@{}cccc@{}}a_{1} & \ast & \ast & \ast \\ & a_{2} & \ast & \ast \\ & & a_{3} & \ast \\ & & & a_{4}\end{array}\right]\right)=|a_{1}^{3}a_{2}a_{3}^{-1}a_{4}^{-3}|_{p},\end{eqnarray}$$ where ![]() $|\ast |_{p}$ denotes the
$|\ast |_{p}$ denotes the ![]() $p$-adic absolute value. The unramified principal representation corresponding to
$p$-adic absolute value. The unramified principal representation corresponding to ![]() ${\it\chi}$ is given by
${\it\chi}$ is given by ![]() $I({\it\chi})$, which consists of locally constant functions
$I({\it\chi})$, which consists of locally constant functions 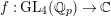 $f:\text{GL}_{4}(\mathbb{Q}_{p})\rightarrow \mathbb{C}$, satisfying
$f:\text{GL}_{4}(\mathbb{Q}_{p})\rightarrow \mathbb{C}$, satisfying
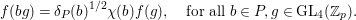 $$\begin{eqnarray}f(bg)={\it\delta}_{P}(b)^{1/2}{\it\chi}(b)f(g),\quad \text{for all }b\in P,g\in \text{GL}_{4}(\mathbb{Z}_{p}).\end{eqnarray}$$
$$\begin{eqnarray}f(bg)={\it\delta}_{P}(b)^{1/2}{\it\chi}(b)f(g),\quad \text{for all }b\in P,g\in \text{GL}_{4}(\mathbb{Z}_{p}).\end{eqnarray}$$ The action of the Hecke algebra is as follows. If 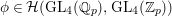 ${\it\phi}\in {\mathcal{H}}(\text{GL}_{4}(\mathbb{Q}_{p}),\text{GL}_{4}(\mathbb{Z}_{p}))$ and
${\it\phi}\in {\mathcal{H}}(\text{GL}_{4}(\mathbb{Q}_{p}),\text{GL}_{4}(\mathbb{Z}_{p}))$ and 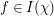 $f\in I({\it\chi})$, define
$f\in I({\it\chi})$, define
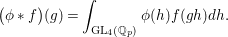 $$\begin{eqnarray}\big({\it\phi}\ast f\big)(g)=\int _{\text{GL}_{4}(\mathbb{Q}_{p})}{\it\phi}(h)f(gh)dh.\end{eqnarray}$$
$$\begin{eqnarray}\big({\it\phi}\ast f\big)(g)=\int _{\text{GL}_{4}(\mathbb{Q}_{p})}{\it\phi}(h)f(gh)dh.\end{eqnarray}$$ Recall that we have normalized the measure ![]() $dh$ on
$dh$ on 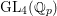 $\text{GL}_{4}(\mathbb{Q}_{p})$ so that the volume of
$\text{GL}_{4}(\mathbb{Q}_{p})$ so that the volume of 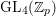 $\text{GL}_{4}(\mathbb{Z}_{p})$ is
$\text{GL}_{4}(\mathbb{Z}_{p})$ is ![]() $1$. Let
$1$. Let ![]() $f=f_{0}$, the unique vector in
$f=f_{0}$, the unique vector in ![]() $I({\it\chi})$ that is right-invariant under
$I({\it\chi})$ that is right-invariant under 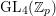 $\text{GL}_{4}(\mathbb{Z}_{p})$ and
$\text{GL}_{4}(\mathbb{Z}_{p})$ and  $f_{0}(1)=1$, and let
$f_{0}(1)=1$, and let ![]() ${\it\phi}={\it\phi}_{h}$, a characteristic function of
${\it\phi}={\it\phi}_{h}$, a characteristic function of  $\text{GL}_{4}(\mathbb{Z}_{p})h\text{GL}_{4}(\mathbb{Z}_{p})=\sqcup _{i}h_{i}\text{GL}_{4}(\mathbb{Z}_{p})$. It follows from (6.3) that
$\text{GL}_{4}(\mathbb{Z}_{p})h\text{GL}_{4}(\mathbb{Z}_{p})=\sqcup _{i}h_{i}\text{GL}_{4}(\mathbb{Z}_{p})$. It follows from (6.3) that
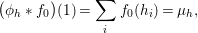 $$\begin{eqnarray}\big({\it\phi}_{h}\ast f_{0}\big)(1)=\mathop{\sum }_{i}f_{0}(h_{i})={\it\mu}_{h},\end{eqnarray}$$
$$\begin{eqnarray}\big({\it\phi}_{h}\ast f_{0}\big)(1)=\mathop{\sum }_{i}f_{0}(h_{i})={\it\mu}_{h},\end{eqnarray}$$ where ![]() ${\it\mu}_{h}$ is determined by the representation
${\it\mu}_{h}$ is determined by the representation ![]() ${\it\pi}_{p}$. The Hecke algebra
${\it\pi}_{p}$. The Hecke algebra 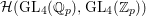 ${\mathcal{H}}(\text{GL}_{4}(\mathbb{Q}_{p}),\text{GL}_{4}(\mathbb{Z}_{p}))$ is generated by
${\mathcal{H}}(\text{GL}_{4}(\mathbb{Q}_{p}),\text{GL}_{4}(\mathbb{Z}_{p}))$ is generated by 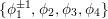 $\{{\it\phi}_{1}^{\pm 1},{\it\phi}_{2},{\it\phi}_{3},{\it\phi}_{4}\}$, defined in (5.2).
$\{{\it\phi}_{1}^{\pm 1},{\it\phi}_{2},{\it\phi}_{3},{\it\phi}_{4}\}$, defined in (5.2).
Lemma 6.1. Let 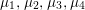 ${\it\mu}_{1},{\it\mu}_{2},{\it\mu}_{3},{\it\mu}_{4}$ be the constants obtained by the action of
${\it\mu}_{1},{\it\mu}_{2},{\it\mu}_{3},{\it\mu}_{4}$ be the constants obtained by the action of 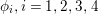 ${\it\phi}_{i},i=1,2,3,4$, on the spherical vector
${\it\phi}_{i},i=1,2,3,4$, on the spherical vector ![]() $f_{0}$ in
$f_{0}$ in ![]() ${\it\pi}_{p}$ according to (6.4). Then
${\it\pi}_{p}$ according to (6.4). Then 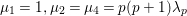 ${\it\mu}_{1}=1,{\it\mu}_{2}={\it\mu}_{4}=p(p+1){\it\lambda}_{p}$ and
${\it\mu}_{1}=1,{\it\mu}_{2}={\it\mu}_{4}=p(p+1){\it\lambda}_{p}$ and 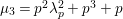 ${\it\mu}_{3}=p^{2}{\it\lambda}_{p}^{2}+p^{3}+p$.
${\it\mu}_{3}=p^{2}{\it\lambda}_{p}^{2}+p^{3}+p$.
Proof. The lemma follows from the fact that the action of the ![]() $p$-adic Hecke algebra on the spherical vector in
$p$-adic Hecke algebra on the spherical vector in ![]() ${\it\pi}_{p}$ is exactly the same as that on
${\it\pi}_{p}$ is exactly the same as that on ![]() $F$ (or
$F$ (or ![]() ${\rm\Phi}_{F}$). First note that
${\rm\Phi}_{F}$). First note that ![]() ${\it\phi}_{1}$ acts as the identity operator, which implies that
${\it\phi}_{1}$ acts as the identity operator, which implies that ![]() ${\it\mu}_{1}=1$. The other Hecke eigenvalues follow from Propositions 5.11 and 5.12.◻
${\it\mu}_{1}=1$. The other Hecke eigenvalues follow from Propositions 5.11 and 5.12.◻
Recall that Proposition 5.5 gives the double coset decompositions which can be used to determine the action of ![]() ${\it\phi}$ on
${\it\phi}$ on ![]() $f_{0}$. Let us abbreviate
$f_{0}$. Let us abbreviate 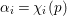 ${\it\alpha}_{i}={\it\chi}_{i}(p)$ for
${\it\alpha}_{i}={\it\chi}_{i}(p)$ for 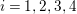 $i=1,2,3,4$. Working in the induced model
$i=1,2,3,4$. Working in the induced model ![]() $I({\it\chi})$ of
$I({\it\chi})$ of ![]() ${\it\pi}_{p}$, we see that
${\it\pi}_{p}$, we see that
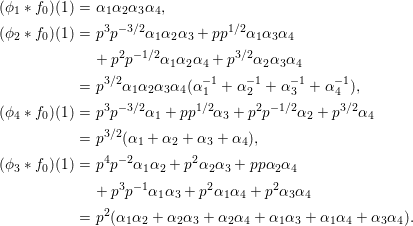 $$\begin{eqnarray}\displaystyle ({\it\phi}_{1}\ast f_{0})(1) & = & \displaystyle {\it\alpha}_{1}{\it\alpha}_{2}{\it\alpha}_{3}{\it\alpha}_{4},\nonumber\\ \displaystyle ({\it\phi}_{2}\ast f_{0})(1) & = & \displaystyle p^{3}p^{-3/2}{\it\alpha}_{1}{\it\alpha}_{2}{\it\alpha}_{3}+pp^{1/2}{\it\alpha}_{1}{\it\alpha}_{3}{\it\alpha}_{4}\nonumber\\ \displaystyle & & \displaystyle +\,p^{2}p^{-1/2}{\it\alpha}_{1}{\it\alpha}_{2}{\it\alpha}_{4}+p^{3/2}{\it\alpha}_{2}{\it\alpha}_{3}{\it\alpha}_{4}\nonumber\\ \displaystyle & = & \displaystyle p^{3/2}{\it\alpha}_{1}{\it\alpha}_{2}{\it\alpha}_{3}{\it\alpha}_{4}({\it\alpha}_{1}^{-1}+{\it\alpha}_{2}^{-1}+{\it\alpha}_{3}^{-1}+{\it\alpha}_{4}^{-1}),\nonumber\\ \displaystyle ({\it\phi}_{4}\ast f_{0})(1) & = & \displaystyle p^{3}p^{-3/2}{\it\alpha}_{1}+pp^{1/2}{\it\alpha}_{3}+p^{2}p^{-1/2}{\it\alpha}_{2}+p^{3/2}{\it\alpha}_{4}\nonumber\\ \displaystyle & = & \displaystyle p^{3/2}({\it\alpha}_{1}+{\it\alpha}_{2}+{\it\alpha}_{3}+{\it\alpha}_{4}),\nonumber\\ \displaystyle ({\it\phi}_{3}\ast f_{0})(1) & = & \displaystyle p^{4}p^{-2}{\it\alpha}_{1}{\it\alpha}_{2}+p^{2}{\it\alpha}_{2}{\it\alpha}_{3}+pp{\it\alpha}_{2}{\it\alpha}_{4}\nonumber\\ \displaystyle & & \displaystyle +\,p^{3}p^{-1}{\it\alpha}_{1}{\it\alpha}_{3}+p^{2}{\it\alpha}_{1}{\it\alpha}_{4}+p^{2}{\it\alpha}_{3}{\it\alpha}_{4}\nonumber\\ \displaystyle & = & \displaystyle p^{2}({\it\alpha}_{1}{\it\alpha}_{2}+{\it\alpha}_{2}{\it\alpha}_{3}+{\it\alpha}_{2}{\it\alpha}_{4}+{\it\alpha}_{1}{\it\alpha}_{3}+{\it\alpha}_{1}{\it\alpha}_{4}+{\it\alpha}_{3}{\it\alpha}_{4}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\it\phi}_{1}\ast f_{0})(1) & = & \displaystyle {\it\alpha}_{1}{\it\alpha}_{2}{\it\alpha}_{3}{\it\alpha}_{4},\nonumber\\ \displaystyle ({\it\phi}_{2}\ast f_{0})(1) & = & \displaystyle p^{3}p^{-3/2}{\it\alpha}_{1}{\it\alpha}_{2}{\it\alpha}_{3}+pp^{1/2}{\it\alpha}_{1}{\it\alpha}_{3}{\it\alpha}_{4}\nonumber\\ \displaystyle & & \displaystyle +\,p^{2}p^{-1/2}{\it\alpha}_{1}{\it\alpha}_{2}{\it\alpha}_{4}+p^{3/2}{\it\alpha}_{2}{\it\alpha}_{3}{\it\alpha}_{4}\nonumber\\ \displaystyle & = & \displaystyle p^{3/2}{\it\alpha}_{1}{\it\alpha}_{2}{\it\alpha}_{3}{\it\alpha}_{4}({\it\alpha}_{1}^{-1}+{\it\alpha}_{2}^{-1}+{\it\alpha}_{3}^{-1}+{\it\alpha}_{4}^{-1}),\nonumber\\ \displaystyle ({\it\phi}_{4}\ast f_{0})(1) & = & \displaystyle p^{3}p^{-3/2}{\it\alpha}_{1}+pp^{1/2}{\it\alpha}_{3}+p^{2}p^{-1/2}{\it\alpha}_{2}+p^{3/2}{\it\alpha}_{4}\nonumber\\ \displaystyle & = & \displaystyle p^{3/2}({\it\alpha}_{1}+{\it\alpha}_{2}+{\it\alpha}_{3}+{\it\alpha}_{4}),\nonumber\\ \displaystyle ({\it\phi}_{3}\ast f_{0})(1) & = & \displaystyle p^{4}p^{-2}{\it\alpha}_{1}{\it\alpha}_{2}+p^{2}{\it\alpha}_{2}{\it\alpha}_{3}+pp{\it\alpha}_{2}{\it\alpha}_{4}\nonumber\\ \displaystyle & & \displaystyle +\,p^{3}p^{-1}{\it\alpha}_{1}{\it\alpha}_{3}+p^{2}{\it\alpha}_{1}{\it\alpha}_{4}+p^{2}{\it\alpha}_{3}{\it\alpha}_{4}\nonumber\\ \displaystyle & = & \displaystyle p^{2}({\it\alpha}_{1}{\it\alpha}_{2}+{\it\alpha}_{2}{\it\alpha}_{3}+{\it\alpha}_{2}{\it\alpha}_{4}+{\it\alpha}_{1}{\it\alpha}_{3}+{\it\alpha}_{1}{\it\alpha}_{4}+{\it\alpha}_{3}{\it\alpha}_{4}).\end{eqnarray}$$Proposition 6.2. Let 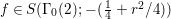 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue ![]() ${\it\lambda}_{p}$ for every odd prime
${\it\lambda}_{p}$ for every odd prime ![]() $p$. Let
$p$. Let ![]() $F=F_{f}$ be as defined in Theorem 4.4. Let
$F=F_{f}$ be as defined in Theorem 4.4. Let 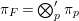 ${\it\pi}_{F}=\otimes _{p}^{\prime }{\it\pi}_{p}$ be the corresponding irreducible cuspidal automorphic representation of
${\it\pi}_{F}=\otimes _{p}^{\prime }{\it\pi}_{p}$ be the corresponding irreducible cuspidal automorphic representation of ![]() ${\mathcal{G}}(\mathbb{A})$. For an odd prime
${\mathcal{G}}(\mathbb{A})$. For an odd prime ![]() $p$, the representation
$p$, the representation ![]() ${\it\pi}_{p}$ is the unique spherical constituent of the unramified principal series representation
${\it\pi}_{p}$ is the unique spherical constituent of the unramified principal series representation ![]() $I({\it\chi})$, where, up to the action of the Weyl group of
$I({\it\chi})$, where, up to the action of the Weyl group of ![]() $\text{GL}_{4}$, the character
$\text{GL}_{4}$, the character ![]() ${\it\chi}$ is given by
${\it\chi}$ is given by
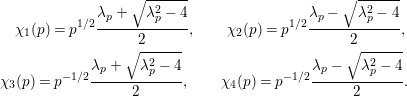 $$\begin{eqnarray}\displaystyle {\it\chi}_{1}(p)=p^{1/2}\frac{{\it\lambda}_{p}+\sqrt{{\it\lambda}_{p}^{2}-4}}{2},\qquad {\it\chi}_{2}(p)=p^{1/2}\frac{{\it\lambda}_{p}-\sqrt{{\it\lambda}_{p}^{2}-4}}{2}, & & \displaystyle \nonumber\\ \displaystyle {\it\chi}_{3}(p)=p^{-1/2}\frac{{\it\lambda}_{p}+\sqrt{{\it\lambda}_{p}^{2}-4}}{2},\qquad {\it\chi}_{4}(p)=p^{-1/2}\frac{{\it\lambda}_{p}-\sqrt{{\it\lambda}_{p}^{2}-4}}{2}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\chi}_{1}(p)=p^{1/2}\frac{{\it\lambda}_{p}+\sqrt{{\it\lambda}_{p}^{2}-4}}{2},\qquad {\it\chi}_{2}(p)=p^{1/2}\frac{{\it\lambda}_{p}-\sqrt{{\it\lambda}_{p}^{2}-4}}{2}, & & \displaystyle \nonumber\\ \displaystyle {\it\chi}_{3}(p)=p^{-1/2}\frac{{\it\lambda}_{p}+\sqrt{{\it\lambda}_{p}^{2}-4}}{2},\qquad {\it\chi}_{4}(p)=p^{-1/2}\frac{{\it\lambda}_{p}-\sqrt{{\it\lambda}_{p}^{2}-4}}{2}. & & \displaystyle\end{eqnarray}$$Proof. The representation ![]() $I({\it\chi})$ corresponding to
$I({\it\chi})$ corresponding to ![]() ${\it\pi}_{p}$ is generated by the spherical vector
${\it\pi}_{p}$ is generated by the spherical vector ![]() $f_{0}$, and, hence, it is completely determined by the action of the generators of the Hecke algebra on
$f_{0}$, and, hence, it is completely determined by the action of the generators of the Hecke algebra on ![]() $f_{0}$. The representation
$f_{0}$. The representation ![]() ${\it\pi}_{p}$ is also determined by the Hecke eigenvalues of
${\it\pi}_{p}$ is also determined by the Hecke eigenvalues of ![]() $F$ (or
$F$ (or ![]() ${\rm\Phi}_{F}$) under the Hecke algebra
${\rm\Phi}_{F}$) under the Hecke algebra 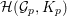 ${\mathcal{H}}({\mathcal{G}}_{p},K_{p})$. Substituting the values of
${\mathcal{H}}({\mathcal{G}}_{p},K_{p})$. Substituting the values of 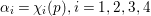 ${\it\alpha}_{i}={\it\chi}_{i}(p),i=1,2,3,4$, from (6.6) into (6.5) shows that we get the exact same eigenvalues as in Lemma 6.1. This completes the proof of the proposition.◻
${\it\alpha}_{i}={\it\chi}_{i}(p),i=1,2,3,4$, from (6.6) into (6.5) shows that we get the exact same eigenvalues as in Lemma 6.1. This completes the proof of the proposition.◻
Let us remark here that we can use Lemma 6.1 to directly solve for ![]() ${\it\alpha}_{i}$ from (6.5). It is a tedious computation but results in the same answer as in the statement of the above proposition.
${\it\alpha}_{i}$ from (6.5). It is a tedious computation but results in the same answer as in the statement of the above proposition.
Description of ![]() ${\it\pi}_{2}$
${\it\pi}_{2}$
Recall that  $B_{2}=B\otimes _{\mathbb{Q}}\mathbb{Q}_{2}$, where
$B_{2}=B\otimes _{\mathbb{Q}}\mathbb{Q}_{2}$, where ![]() $B$ is a definite quaternion algebra over
$B$ is a definite quaternion algebra over ![]() $\mathbb{Q}$ with discriminant
$\mathbb{Q}$ with discriminant ![]() $2$, and
$2$, and ![]() ${\mathcal{O}}_{2}$ is the completion of the Hurwitz order
${\mathcal{O}}_{2}$ is the completion of the Hurwitz order ![]() ${\mathcal{O}}$ at
${\mathcal{O}}$ at ![]() $2$. In this case,
$2$. In this case, 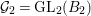 ${\mathcal{G}}_{2}=\text{GL}_{2}(B_{2})$ and
${\mathcal{G}}_{2}=\text{GL}_{2}(B_{2})$ and 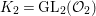 $K_{2}=\text{GL}_{2}({\mathcal{O}}_{2})$. Given two unramified characters
$K_{2}=\text{GL}_{2}({\mathcal{O}}_{2})$. Given two unramified characters ![]() ${\it\chi}_{1},{\it\chi}_{2}$ of
${\it\chi}_{1},{\it\chi}_{2}$ of ![]() $B_{2}^{\times }$, we obtain a character
$B_{2}^{\times }$, we obtain a character ![]() ${\it\chi}$ of the Borel subgroup of upper triangular matrices on
${\it\chi}$ of the Borel subgroup of upper triangular matrices on ![]() ${\mathcal{G}}$ by
${\mathcal{G}}$ by
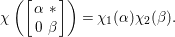 $$\begin{eqnarray}{\it\chi}\left(\left[\begin{array}{@{}cc@{}}{\it\alpha} & \ast \\ 0 & {\it\beta}\end{array}\right]\right)={\it\chi}_{1}({\it\alpha}){\it\chi}_{2}({\it\beta}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\chi}\left(\left[\begin{array}{@{}cc@{}}{\it\alpha} & \ast \\ 0 & {\it\beta}\end{array}\right]\right)={\it\chi}_{1}({\it\alpha}){\it\chi}_{2}({\it\beta}).\end{eqnarray}$$The modulus character is given by
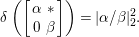 $$\begin{eqnarray}{\it\delta}\left(\left[\begin{array}{@{}cc@{}}{\it\alpha} & \ast \\ 0 & {\it\beta}\end{array}\right]\right)=|{\it\alpha}/{\it\beta}|_{2}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}\left(\left[\begin{array}{@{}cc@{}}{\it\alpha} & \ast \\ 0 & {\it\beta}\end{array}\right]\right)=|{\it\alpha}/{\it\beta}|_{2}^{2}.\end{eqnarray}$$ Here, ![]() $|\,|_{2}$ is the
$|\,|_{2}$ is the ![]() $2$-adic absolute value of the reduced norm of
$2$-adic absolute value of the reduced norm of ![]() $B_{2}$. The unramified principal series representation corresponding to
$B_{2}$. The unramified principal series representation corresponding to ![]() ${\it\chi}$ is given by
${\it\chi}$ is given by ![]() $I({\it\chi})$, which consists of locally constant functions
$I({\it\chi})$, which consists of locally constant functions 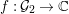 $f:{\mathcal{G}}_{2}\rightarrow \mathbb{C}$, satisfying
$f:{\mathcal{G}}_{2}\rightarrow \mathbb{C}$, satisfying
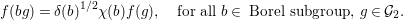 $$\begin{eqnarray}f(bg)={\it\delta}(b)^{1/2}{\it\chi}(b)f(g),\quad \text{for all }b\in \text{Borel subgroup, }g\in {\mathcal{G}}_{2}.\end{eqnarray}$$
$$\begin{eqnarray}f(bg)={\it\delta}(b)^{1/2}{\it\chi}(b)f(g),\quad \text{for all }b\in \text{Borel subgroup, }g\in {\mathcal{G}}_{2}.\end{eqnarray}$$ The action of the Hecke algebra is as follows. If 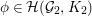 ${\it\phi}\in {\mathcal{H}}({\mathcal{G}}_{2},K_{2})$ and
${\it\phi}\in {\mathcal{H}}({\mathcal{G}}_{2},K_{2})$ and 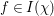 $f\in I({\it\chi})$, define
$f\in I({\it\chi})$, define
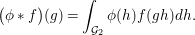 $$\begin{eqnarray}\big({\it\phi}\ast f\big)(g)=\int _{{\mathcal{G}}_{2}}{\it\phi}(h)f(gh)dh.\end{eqnarray}$$
$$\begin{eqnarray}\big({\it\phi}\ast f\big)(g)=\int _{{\mathcal{G}}_{2}}{\it\phi}(h)f(gh)dh.\end{eqnarray}$$ Recall that we have normalized the measure ![]() $dh$ on
$dh$ on ![]() ${\mathcal{G}}_{2}$ so that the volume of
${\mathcal{G}}_{2}$ so that the volume of ![]() $K_{2}$ is
$K_{2}$ is ![]() $1$. Let
$1$. Let ![]() $f=f_{0}$, the unique vector in
$f=f_{0}$, the unique vector in ![]() $I({\it\chi})$ that is right-invariant under
$I({\it\chi})$ that is right-invariant under ![]() $K_{2}$ and
$K_{2}$ and 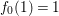 $f_{0}(1)=1$, and let
$f_{0}(1)=1$, and let ![]() ${\it\phi}={\it\phi}_{h}$, a characteristic function of
${\it\phi}={\it\phi}_{h}$, a characteristic function of 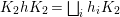 $K_{2}hK_{2}=\sqcup _{i}h_{i}K_{2}$. It follows from (6.3) that
$K_{2}hK_{2}=\sqcup _{i}h_{i}K_{2}$. It follows from (6.3) that
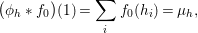 $$\begin{eqnarray}\big({\it\phi}_{h}\ast f_{0}\big)(1)=\mathop{\sum }_{i}f_{0}(h_{i})={\it\mu}_{h},\end{eqnarray}$$
$$\begin{eqnarray}\big({\it\phi}_{h}\ast f_{0}\big)(1)=\mathop{\sum }_{i}f_{0}(h_{i})={\it\mu}_{h},\end{eqnarray}$$ where ![]() ${\it\mu}_{h}$ is determined by the representation
${\it\mu}_{h}$ is determined by the representation ![]() ${\it\pi}_{2}$. The Hecke algebra
${\it\pi}_{2}$. The Hecke algebra 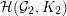 ${\mathcal{H}}({\mathcal{G}}_{2},K_{2})$ is generated by
${\mathcal{H}}({\mathcal{G}}_{2},K_{2})$ is generated by 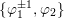 $\{{\it\varphi}_{1}^{\pm 1},{\it\varphi}_{2}\}$, where
$\{{\it\varphi}_{1}^{\pm 1},{\it\varphi}_{2}\}$, where ![]() ${\it\varphi}_{1},~{\it\varphi}_{2}$ denote the characteristic functions for
${\it\varphi}_{1},~{\it\varphi}_{2}$ denote the characteristic functions for
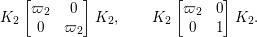 $$\begin{eqnarray}K_{2}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & 0\\ 0 & {\it\varpi}_{2}\end{array}\right]K_{2},\qquad K_{2}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & 0\\ 0 & 1\end{array}\right]K_{2}.\end{eqnarray}$$
$$\begin{eqnarray}K_{2}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & 0\\ 0 & {\it\varpi}_{2}\end{array}\right]K_{2},\qquad K_{2}\left[\begin{array}{@{}cc@{}}{\it\varpi}_{2} & 0\\ 0 & 1\end{array}\right]K_{2}.\end{eqnarray}$$ Here, ![]() ${\it\varpi}_{2}$ is a uniformizer for
${\it\varpi}_{2}$ is a uniformizer for ![]() $B_{2}$.
$B_{2}$.
Lemma 6.3. Let ![]() ${\it\mu}_{1},{\it\mu}_{2}$ be the constants obtained by the action of
${\it\mu}_{1},{\it\mu}_{2}$ be the constants obtained by the action of  ${\it\phi}_{i},i=1,2$, on the spherical vector
${\it\phi}_{i},i=1,2$, on the spherical vector ![]() $f_{0}$ in
$f_{0}$ in ![]() ${\it\pi}_{2}$ according to (6.8). Then
${\it\pi}_{2}$ according to (6.8). Then ![]() ${\it\mu}_{1}=1$ and
${\it\mu}_{1}=1$ and 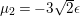 ${\it\mu}_{2}=-3\sqrt{2}{\it\epsilon}$, where
${\it\mu}_{2}=-3\sqrt{2}{\it\epsilon}$, where ![]() ${\it\epsilon}$ is the Atkin–Lehner eigenvalue of
${\it\epsilon}$ is the Atkin–Lehner eigenvalue of ![]() $f$.
$f$.
Proof. The proof is the same as in the case of an odd prime. ◻
Recall that Proposition 5.5 gives the double coset decompositions which can be used to determine the action of ![]() ${\it\phi}$ on
${\it\phi}$ on ![]() $f_{0}$. Let us abbreviate
$f_{0}$. Let us abbreviate 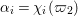 ${\it\alpha}_{i}={\it\chi}_{i}({\it\varpi}_{2})$ for
${\it\alpha}_{i}={\it\chi}_{i}({\it\varpi}_{2})$ for ![]() $i=1,2$. Working in the induced model
$i=1,2$. Working in the induced model ![]() $I({\it\chi})$ of
$I({\it\chi})$ of ![]() ${\it\pi}_{2}$, we see that
${\it\pi}_{2}$, we see that
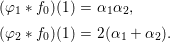 $$\begin{eqnarray}\displaystyle ({\it\varphi}_{1}\ast f_{0})(1) & = & \displaystyle {\it\alpha}_{1}{\it\alpha}_{2},\nonumber\\ \displaystyle ({\it\varphi}_{2}\ast f_{0})(1) & = & \displaystyle 2({\it\alpha}_{1}+{\it\alpha}_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\it\varphi}_{1}\ast f_{0})(1) & = & \displaystyle {\it\alpha}_{1}{\it\alpha}_{2},\nonumber\\ \displaystyle ({\it\varphi}_{2}\ast f_{0})(1) & = & \displaystyle 2({\it\alpha}_{1}+{\it\alpha}_{2}).\end{eqnarray}$$Proposition 6.4. Let 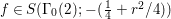 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a new form with Hecke eigenvalue
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a new form with Hecke eigenvalue ![]() ${\it\lambda}_{p}$ for
${\it\lambda}_{p}$ for ![]() $p=2$ and Atkin–Lehner eigenvalue
$p=2$ and Atkin–Lehner eigenvalue ![]() ${\it\epsilon}$, for which
${\it\epsilon}$, for which 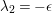 ${\it\lambda}_{2}=-{\it\epsilon}$ holds (cf. (5.5)). Let
${\it\lambda}_{2}=-{\it\epsilon}$ holds (cf. (5.5)). Let ![]() $F=F_{f}$ be as defined in Theorem 4.4. Let
$F=F_{f}$ be as defined in Theorem 4.4. Let 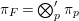 ${\it\pi}_{F}=\otimes _{p}^{\prime }{\it\pi}_{p}$ be the corresponding irreducible cuspidal automorphic representation of
${\it\pi}_{F}=\otimes _{p}^{\prime }{\it\pi}_{p}$ be the corresponding irreducible cuspidal automorphic representation of ![]() ${\mathcal{G}}(\mathbb{A})$. The representation
${\mathcal{G}}(\mathbb{A})$. The representation ![]() ${\it\pi}_{2}$ is the unique spherical constituent of the unramified principal series representation
${\it\pi}_{2}$ is the unique spherical constituent of the unramified principal series representation ![]() $I({\it\chi})$, where, up to the action of the Weyl group, the character
$I({\it\chi})$, where, up to the action of the Weyl group, the character ![]() ${\it\chi}$ is given by
${\it\chi}$ is given by
 $$\begin{eqnarray}{\it\chi}_{1}({\it\varpi}_{2})=-\sqrt{2}{\it\epsilon},\qquad {\it\chi}_{2}({\it\varpi}_{2})=-1/\sqrt{2}{\it\epsilon}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\chi}_{1}({\it\varpi}_{2})=-\sqrt{2}{\it\epsilon},\qquad {\it\chi}_{2}({\it\varpi}_{2})=-1/\sqrt{2}{\it\epsilon}.\end{eqnarray}$$Proof. The proof is the same as in the case of an odd prime. ◻
Description of ![]() ${\it\pi}_{\infty }$
${\it\pi}_{\infty }$
We now determine ![]() ${\it\pi}_{\infty }$. We note that
${\it\pi}_{\infty }$. We note that 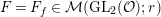 $F=F_{f}\in {\mathcal{M}}(\text{GL}_{2}({\mathcal{O}});r)$ implies that the archimedean component
$F=F_{f}\in {\mathcal{M}}(\text{GL}_{2}({\mathcal{O}});r)$ implies that the archimedean component ![]() ${\it\pi}_{\infty }$ of
${\it\pi}_{\infty }$ of ![]() ${\it\pi}_{F}$ is spherical. Namely,
${\it\pi}_{F}$ is spherical. Namely, ![]() ${\it\pi}_{\infty }$ has a
${\it\pi}_{\infty }$ has a ![]() $K_{\infty }$-invariant vector, where we put
$K_{\infty }$-invariant vector, where we put  $K_{\infty }:=K$ with
$K_{\infty }:=K$ with ![]() $K$ as in (2.1). In fact, up to constant multiples, such a vector is unique for
$K$ as in (2.1). In fact, up to constant multiples, such a vector is unique for ![]() ${\it\pi}_{\infty }$, as we soon see.
${\it\pi}_{\infty }$, as we soon see.
We now introduce 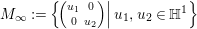 $M_{\infty }:=\left\{\!\left.\left(\!\begin{smallmatrix}u_{1} & 0\phantom{}\\ 0 & u_{2}\end{smallmatrix}\!\right)\right|u_{1},u_{2}\in \mathbb{H}^{1}\right\}$ (see Section 2.1 for
$M_{\infty }:=\left\{\!\left.\left(\!\begin{smallmatrix}u_{1} & 0\phantom{}\\ 0 & u_{2}\end{smallmatrix}\!\right)\right|u_{1},u_{2}\in \mathbb{H}^{1}\right\}$ (see Section 2.1 for ![]() $\mathbb{H}^{1}$). Let
$\mathbb{H}^{1}$). Let ![]() $P_{\infty }$ be the standard proper parabolic subgroup
$P_{\infty }$ be the standard proper parabolic subgroup 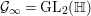 ${\mathcal{G}}_{\infty }=\text{GL}_{2}(\mathbb{H})$ given by
${\mathcal{G}}_{\infty }=\text{GL}_{2}(\mathbb{H})$ given by
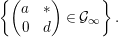 $$\begin{eqnarray}\left\{\left(\begin{array}{@{}cc@{}}a & \ast \\ 0 & d\end{array}\right)\in {\mathcal{G}}_{\infty }\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\left(\begin{array}{@{}cc@{}}a & \ast \\ 0 & d\end{array}\right)\in {\mathcal{G}}_{\infty }\right\}.\end{eqnarray}$$ We have 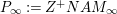 $P_{\infty }:=Z^{+}NAM_{\infty }$, where
$P_{\infty }:=Z^{+}NAM_{\infty }$, where ![]() $Z^{+},~N$ and
$Z^{+},~N$ and ![]() $A$ are as in (2.1). The group
$A$ are as in (2.1). The group 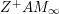 $Z^{+}AM_{\infty }$ is nothing but the Levi subgroup of
$Z^{+}AM_{\infty }$ is nothing but the Levi subgroup of ![]() $P_{\infty }$. We now note that the Langlands classification of real reductive groups (cf. [Reference Langlands18]) implies that
$P_{\infty }$. We now note that the Langlands classification of real reductive groups (cf. [Reference Langlands18]) implies that ![]() ${\it\pi}_{\infty }$ has to be embedded into some principal series representation
${\it\pi}_{\infty }$ has to be embedded into some principal series representation ![]() $I_{P_{\infty }}$ of
$I_{P_{\infty }}$ of ![]() ${\mathcal{G}}_{\infty }$ induced from a quasicharacter of
${\mathcal{G}}_{\infty }$ induced from a quasicharacter of ![]() $P_{\infty }$. Since
$P_{\infty }$. Since ![]() ${\it\pi}_{\infty }$ is spherical,
${\it\pi}_{\infty }$ is spherical, ![]() $I_{P_{\infty }}$ is also spherical. As
$I_{P_{\infty }}$ is also spherical. As ![]() ${\it\pi}_{\infty }$ has the trivial central character, so does
${\it\pi}_{\infty }$ has the trivial central character, so does ![]() $I_{P_{\infty }}$. Combining these with the Frobenius reciprocity for compact Lie groups (cf. [Reference Knapp15, Theorem 9.9]), one can verify that the quasicharacter of
$I_{P_{\infty }}$. Combining these with the Frobenius reciprocity for compact Lie groups (cf. [Reference Knapp15, Theorem 9.9]), one can verify that the quasicharacter of ![]() $P_{\infty }$ inducing
$P_{\infty }$ inducing ![]() $I_{P_{\infty }}$ has to be trivial on
$I_{P_{\infty }}$ has to be trivial on ![]() $Z^{+}M_{\infty }$, and that
$Z^{+}M_{\infty }$, and that ![]() $I_{P_{\infty }}$ and
$I_{P_{\infty }}$ and ![]() ${\it\pi}_{\infty }$ have a unique
${\it\pi}_{\infty }$ have a unique ![]() $K_{\infty }$-invariant vector, up to constant multiples. For
$K_{\infty }$-invariant vector, up to constant multiples. For ![]() $s\in \mathbb{C}$ we introduce the quasicharacter
$s\in \mathbb{C}$ we introduce the quasicharacter ![]() ${\it\chi}_{s}$ of
${\it\chi}_{s}$ of ![]() $P_{\infty }$ defined by
$P_{\infty }$ defined by
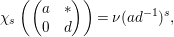 $$\begin{eqnarray}{\it\chi}_{s}\left(\left(\begin{array}{@{}cc@{}}a & \ast \\ 0 & d\end{array}\right)\right)={\it\nu}(ad^{-1})^{s},\end{eqnarray}$$
$$\begin{eqnarray}{\it\chi}_{s}\left(\left(\begin{array}{@{}cc@{}}a & \ast \\ 0 & d\end{array}\right)\right)={\it\nu}(ad^{-1})^{s},\end{eqnarray}$$ where we recall that ![]() ${\it\nu}$ denotes the reduced norm of
${\it\nu}$ denotes the reduced norm of ![]() $\mathbb{H}$ (cf. Section 2.1). We note that the quasicharacters of
$\mathbb{H}$ (cf. Section 2.1). We note that the quasicharacters of ![]() $P_{\infty }$ trivial on
$P_{\infty }$ trivial on ![]() $Z^{+}M_{\infty }$ should be of this form. We furthermore introduce the modulus character
$Z^{+}M_{\infty }$ should be of this form. We furthermore introduce the modulus character ![]() ${\it\delta}_{\infty }$ of
${\it\delta}_{\infty }$ of ![]() $P_{\infty }$. The principal series representation
$P_{\infty }$. The principal series representation ![]() $I_{P_{\infty }}$ is then expressed as
$I_{P_{\infty }}$ is then expressed as
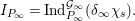 $$\begin{eqnarray}I_{P_{\infty }}=\text{Ind}_{P_{\infty }}^{{\mathcal{G}}_{\infty }}({\it\delta}_{\infty }{\it\chi}_{s}).\end{eqnarray}$$
$$\begin{eqnarray}I_{P_{\infty }}=\text{Ind}_{P_{\infty }}^{{\mathcal{G}}_{\infty }}({\it\delta}_{\infty }{\it\chi}_{s}).\end{eqnarray}$$Proposition 6.5. We have an isomorphism
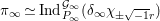 $$\begin{eqnarray}{\it\pi}_{\infty }\simeq \text{Ind}_{P_{\infty }}^{{\mathcal{G}}_{\infty }}({\it\delta}_{\infty }{\it\chi}_{\pm \sqrt{-1}r})\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}_{\infty }\simeq \text{Ind}_{P_{\infty }}^{{\mathcal{G}}_{\infty }}({\it\delta}_{\infty }{\it\chi}_{\pm \sqrt{-1}r})\end{eqnarray}$$ as 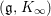 $(\mathfrak{g},K_{\infty })$-modules, where we recall that
$(\mathfrak{g},K_{\infty })$-modules, where we recall that ![]() $\mathfrak{g}$ denotes the Lie algebra of
$\mathfrak{g}$ denotes the Lie algebra of ![]() ${\mathcal{G}}_{\infty }$ (cf. Section2.2).
${\mathcal{G}}_{\infty }$ (cf. Section2.2).
Proof. Let ![]() $v$ be a unique
$v$ be a unique ![]() $K_{\infty }$-invariant vector in the representation space of
$K_{\infty }$-invariant vector in the representation space of 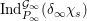 $\text{Ind}_{P_{\infty }}^{{\mathcal{G}}_{\infty }}({\it\delta}_{\infty }{\it\chi}_{s})$, which
$\text{Ind}_{P_{\infty }}^{{\mathcal{G}}_{\infty }}({\it\delta}_{\infty }{\it\chi}_{s})$, which ![]() ${\it\pi}_{\infty }$ can be embedded into. Then,
${\it\pi}_{\infty }$ can be embedded into. Then, ![]() $v$ can also be regarded as a vector of
$v$ can also be regarded as a vector of ![]() ${\it\pi}_{\infty }$. We remark that
${\it\pi}_{\infty }$. We remark that ![]() ${\it\pi}_{\infty }$ can be viewed as a representation of
${\it\pi}_{\infty }$ can be viewed as a representation of 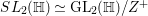 $SL_{2}(\mathbb{H})\simeq \text{GL}_{2}(\mathbb{H})/Z^{+}$ (cf. Section 2.2) since it has the trivial central character. Consider the infinitesimal action of the Casimir operator
$SL_{2}(\mathbb{H})\simeq \text{GL}_{2}(\mathbb{H})/Z^{+}$ (cf. Section 2.2) since it has the trivial central character. Consider the infinitesimal action of the Casimir operator ![]() ${\rm\Omega}$ (cf. (2.3)) on
${\rm\Omega}$ (cf. (2.3)) on ![]() $v$. We then have
$v$. We then have
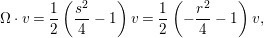 $$\begin{eqnarray}{\rm\Omega}\cdot v=\displaystyle \frac{1}{2}\left(\frac{s^{2}}{4}-1\right)v=\displaystyle \frac{1}{2}\left(-\frac{r^{2}}{4}-1\right)v,\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Omega}\cdot v=\displaystyle \frac{1}{2}\left(\frac{s^{2}}{4}-1\right)v=\displaystyle \frac{1}{2}\left(-\frac{r^{2}}{4}-1\right)v,\end{eqnarray}$$ which leads to 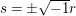 $s=\pm \sqrt{-1}r$. Now recall that we can assume
$s=\pm \sqrt{-1}r$. Now recall that we can assume ![]() $r\in \mathbb{R}$ (cf. Proposition 2.4). We thus know that the quasi-character
$r\in \mathbb{R}$ (cf. Proposition 2.4). We thus know that the quasi-character ![]() ${\it\chi}_{s}$ is parametrized by a purely imaginary number
${\it\chi}_{s}$ is parametrized by a purely imaginary number 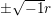 $\pm \sqrt{-1}r$. By Harish-Chandra [Reference Chandra10, §41, Theorem 1], the spherical principal series representation
$\pm \sqrt{-1}r$. By Harish-Chandra [Reference Chandra10, §41, Theorem 1], the spherical principal series representation 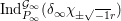 $\text{Ind}_{P_{\infty }}^{{\mathcal{G}}_{\infty }}({\it\delta}_{\infty }{\it\chi}_{\pm \sqrt{-1}r})$ is an irreducible unitary representation. For this see also [Reference Collingwood6, Remark (2.1.13)] and note the accidental isomorphism
$\text{Ind}_{P_{\infty }}^{{\mathcal{G}}_{\infty }}({\it\delta}_{\infty }{\it\chi}_{\pm \sqrt{-1}r})$ is an irreducible unitary representation. For this see also [Reference Collingwood6, Remark (2.1.13)] and note the accidental isomorphism 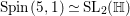 $\text{Spin}(5,1)\simeq \text{SL}_{2}(\mathbb{H})$ as real Lie groups. Consequently we have the isomorphism in the assertion.◻
$\text{Spin}(5,1)\simeq \text{SL}_{2}(\mathbb{H})$ as real Lie groups. Consequently we have the isomorphism in the assertion.◻
6.2 CAP representations
Let us first give the definition of CAP representations.
Definition 6.6. Let ![]() $G_{1}$ and
$G_{1}$ and ![]() $G_{2}$ be two reductive algebraic groups over a number field such that
$G_{2}$ be two reductive algebraic groups over a number field such that 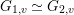 $G_{1,v}\simeq G_{2,v}$ for almost all places
$G_{1,v}\simeq G_{2,v}$ for almost all places ![]() $v$. Let
$v$. Let ![]() $P_{2}$ be a parabolic subgroup of
$P_{2}$ be a parabolic subgroup of ![]() $G_{2}$ with Levi decomposition
$G_{2}$ with Levi decomposition 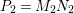 $P_{2}=M_{2}N_{2}$. An irreducible cuspidal automorphic representation
$P_{2}=M_{2}N_{2}$. An irreducible cuspidal automorphic representation 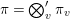 ${\it\pi}=\otimes _{v}^{\prime }{\it\pi}_{v}$ of
${\it\pi}=\otimes _{v}^{\prime }{\it\pi}_{v}$ of ![]() $G_{1}(\mathbb{A})$ is called cuspidal associated to parabolic (CAP)
$G_{1}(\mathbb{A})$ is called cuspidal associated to parabolic (CAP) ![]() $P_{2}$, if there exists an irreducible cuspidal automorphic representation
$P_{2}$, if there exists an irreducible cuspidal automorphic representation ![]() ${\it\sigma}$ of
${\it\sigma}$ of ![]() $M_{2}$ such that
$M_{2}$ such that ![]() ${\it\pi}_{v}\simeq {\it\pi}_{v}^{\prime }$ for almost all places
${\it\pi}_{v}\simeq {\it\pi}_{v}^{\prime }$ for almost all places ![]() $v$, where
$v$, where 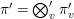 ${\it\pi}^{\prime }=\otimes _{v}^{\prime }{\it\pi}_{v}^{\prime }$ is an irreducible constituent of
${\it\pi}^{\prime }=\otimes _{v}^{\prime }{\it\pi}_{v}^{\prime }$ is an irreducible constituent of 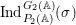 $\text{Ind}_{P_{2}(\mathbb{A})}^{G_{2}(\mathbb{A})}({\it\sigma})$.
$\text{Ind}_{P_{2}(\mathbb{A})}^{G_{2}(\mathbb{A})}({\it\sigma})$.
See [Reference Gan8] and [Reference Pitale22] for details on CAP representations defined for two groups instead of just one. Take 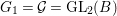 $G_{1}={\mathcal{G}}=\text{GL}_{2}(B)$ and
$G_{1}={\mathcal{G}}=\text{GL}_{2}(B)$ and 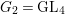 $G_{2}=\text{GL}_{4}$. Here,
$G_{2}=\text{GL}_{4}$. Here, ![]() $B$ is a definite quaternion algebra with discriminant
$B$ is a definite quaternion algebra with discriminant ![]() $2$. Since these groups are inner forms of each other, we have
$2$. Since these groups are inner forms of each other, we have 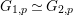 $G_{1,p}\simeq G_{2,p}$ for all odd primes
$G_{1,p}\simeq G_{2,p}$ for all odd primes ![]() $p$. Let
$p$. Let ![]() $P_{2}$ be the standard parabolic of
$P_{2}$ be the standard parabolic of ![]() $\text{GL}_{4}$ with Levi subgroup
$\text{GL}_{4}$ with Levi subgroup 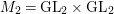 $M_{2}=\text{GL}_{2}\times \text{GL}_{2}$. Let
$M_{2}=\text{GL}_{2}\times \text{GL}_{2}$. Let 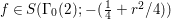 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue ![]() ${\it\lambda}_{p}$ for every odd prime
${\it\lambda}_{p}$ for every odd prime ![]() $p$ and Atkin–Lehner eigenvalue
$p$ and Atkin–Lehner eigenvalue ![]() ${\it\epsilon}$. Let
${\it\epsilon}$. Let 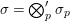 ${\it\sigma}=\otimes _{p}^{\prime }{\it\sigma}_{p}$ be the irreducible cuspidal automorphic representation of
${\it\sigma}=\otimes _{p}^{\prime }{\it\sigma}_{p}$ be the irreducible cuspidal automorphic representation of ![]() $\text{GL}_{2}$ corresponding to
$\text{GL}_{2}$ corresponding to ![]() $f$. For an odd prime
$f$. For an odd prime ![]() $p$, the representation
$p$, the representation ![]() ${\it\sigma}_{p}$ is the unramified principal series representation
${\it\sigma}_{p}$ is the unramified principal series representation ![]() $I({\it\eta})$, where
$I({\it\eta})$, where ![]() ${\it\eta}$ is given by
${\it\eta}$ is given by
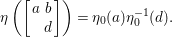 $$\begin{eqnarray}{\it\eta}\left(\left[\begin{array}{@{}cc@{}}a & b\\ & d\end{array}\right]\right)={\it\eta}_{0}(a){\it\eta}_{0}^{-1}(d).\end{eqnarray}$$
$$\begin{eqnarray}{\it\eta}\left(\left[\begin{array}{@{}cc@{}}a & b\\ & d\end{array}\right]\right)={\it\eta}_{0}(a){\it\eta}_{0}^{-1}(d).\end{eqnarray}$$ Here, ![]() ${\it\eta}_{0}$ is an unramified character of
${\it\eta}_{0}$ is an unramified character of ![]() $\mathbb{Q}_{p}^{\times }$ such that
$\mathbb{Q}_{p}^{\times }$ such that 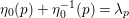 ${\it\eta}_{0}(p)+{\it\eta}_{0}^{-1}(p)={\it\lambda}_{p}$. For
${\it\eta}_{0}(p)+{\it\eta}_{0}^{-1}(p)={\it\lambda}_{p}$. For ![]() $p=2$ assume that
$p=2$ assume that ![]() $f$ is a new form. Then, the representation
$f$ is a new form. Then, the representation ![]() ${\it\sigma}_{2}$ is the twist of the Steinberg representation of
${\it\sigma}_{2}$ is the twist of the Steinberg representation of 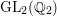 $\text{GL}_{2}(\mathbb{Q}_{2})$ by an unramified character
$\text{GL}_{2}(\mathbb{Q}_{2})$ by an unramified character ![]() ${\it\eta}^{\prime }$, with
${\it\eta}^{\prime }$, with 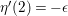 ${\it\eta}^{\prime }(2)=-{\it\epsilon}$. The representation
${\it\eta}^{\prime }(2)=-{\it\epsilon}$. The representation ![]() ${\it\sigma}$ gives a representation
${\it\sigma}$ gives a representation 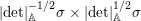 $|\text{det}|_{\mathbb{A}}^{-1/2}{\it\sigma}\times |\text{det}|_{\mathbb{A}}^{1/2}{\it\sigma}$ of
$|\text{det}|_{\mathbb{A}}^{-1/2}{\it\sigma}\times |\text{det}|_{\mathbb{A}}^{1/2}{\it\sigma}$ of ![]() $M_{2}$, where
$M_{2}$, where ![]() $|~|_{\mathbb{A}}$ denotes the idele norm of
$|~|_{\mathbb{A}}$ denotes the idele norm of ![]() $\mathbb{A}^{\times }$. We have the following theorem.
$\mathbb{A}^{\times }$. We have the following theorem.
Theorem 6.7. Let 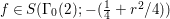 $f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue
$f\in S({\rm\Gamma}_{0}(2);-(\frac{1}{4}+r^{2}/4))$ be a Hecke eigenform with Hecke eigenvalue ![]() ${\it\lambda}_{p}$ for every odd prime
${\it\lambda}_{p}$ for every odd prime ![]() $p$ and Atkin–Lehner eigenvalue
$p$ and Atkin–Lehner eigenvalue ![]() ${\it\epsilon}$. Let
${\it\epsilon}$. Let 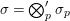 ${\it\sigma}=\otimes _{p}^{\prime }{\it\sigma}_{p}$ be the irreducible cuspidal automorphic representation of
${\it\sigma}=\otimes _{p}^{\prime }{\it\sigma}_{p}$ be the irreducible cuspidal automorphic representation of ![]() $\text{GL}_{2}$ corresponding to
$\text{GL}_{2}$ corresponding to ![]() $f$. Let
$f$. Let ![]() $F=F_{f}$ be as defined in Theorem 4.4. Let
$F=F_{f}$ be as defined in Theorem 4.4. Let 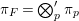 ${\it\pi}_{F}=\otimes _{p}^{\prime }{\it\pi}_{p}$ be the corresponding irreducible cuspidal automorphic representation of
${\it\pi}_{F}=\otimes _{p}^{\prime }{\it\pi}_{p}$ be the corresponding irreducible cuspidal automorphic representation of ![]() ${\mathcal{G}}(\mathbb{A})$. Then
${\mathcal{G}}(\mathbb{A})$. Then ![]() ${\it\pi}_{F}$ is CAP to an irreducible constituent of
${\it\pi}_{F}$ is CAP to an irreducible constituent of 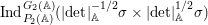 $\text{Ind}_{P_{2}(\mathbb{A})}^{G_{2}(\mathbb{A})}(|\text{det}|_{\mathbb{A}}^{-1/2}{\it\sigma}\times |\text{det}|_{\mathbb{A}}^{1/2}{\it\sigma})$.
$\text{Ind}_{P_{2}(\mathbb{A})}^{G_{2}(\mathbb{A})}(|\text{det}|_{\mathbb{A}}^{-1/2}{\it\sigma}\times |\text{det}|_{\mathbb{A}}^{1/2}{\it\sigma})$.
Proof. The theorem follows from the observation that, for an odd prime ![]() $p$, we have the isomorphism
$p$, we have the isomorphism 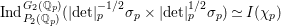 $\text{Ind}_{P_{2}(\mathbb{Q}_{p})}^{G_{2}(\mathbb{Q}_{p})}(|\text{det}|_{p}^{-1/2}{\it\sigma}_{p}\times |\text{det}|_{p}^{1/2}{\it\sigma}_{p})\simeq I({\it\chi}_{p})$. Here,
$\text{Ind}_{P_{2}(\mathbb{Q}_{p})}^{G_{2}(\mathbb{Q}_{p})}(|\text{det}|_{p}^{-1/2}{\it\sigma}_{p}\times |\text{det}|_{p}^{1/2}{\it\sigma}_{p})\simeq I({\it\chi}_{p})$. Here, ![]() $I({\it\chi}_{p})$ is the representation described in Proposition 6.2. A concrete map is given as follows. For
$I({\it\chi}_{p})$ is the representation described in Proposition 6.2. A concrete map is given as follows. For 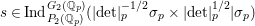 $s\in \text{Ind}_{P_{2}(\mathbb{Q}_{p})}^{G_{2}(\mathbb{Q}_{p})}(|\text{det}|_{p}^{-1/2}{\it\sigma}_{p}\times |\text{det}|_{p}^{1/2}|{\it\sigma}_{p})$ define the function
$s\in \text{Ind}_{P_{2}(\mathbb{Q}_{p})}^{G_{2}(\mathbb{Q}_{p})}(|\text{det}|_{p}^{-1/2}{\it\sigma}_{p}\times |\text{det}|_{p}^{1/2}|{\it\sigma}_{p})$ define the function  $g\mapsto (s(g))(I_{2},I_{2})$. Note that
$g\mapsto (s(g))(I_{2},I_{2})$. Note that  ${\it\delta}_{P_{2}}(\text{diag}(a_{1},a_{2},a_{3},a_{4}))=|a_{1}a_{2}a_{3}^{-1}a_{4}^{-1}|_{p}^{2}$.◻
${\it\delta}_{P_{2}}(\text{diag}(a_{1},a_{2},a_{3},a_{4}))=|a_{1}a_{2}a_{3}^{-1}a_{4}^{-1}|_{p}^{2}$.◻
We can furthermore show that our cuspidal representations ![]() ${\it\pi}_{F}$ provide counterexamples to the Ramanujan conjecture.
${\it\pi}_{F}$ provide counterexamples to the Ramanujan conjecture.
Theorem 6.8. Let 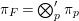 ${\it\pi}_{F}=\otimes _{p}^{\prime }{\it\pi}_{p}$ be as in Theorem 6.7. For every odd prime
${\it\pi}_{F}=\otimes _{p}^{\prime }{\it\pi}_{p}$ be as in Theorem 6.7. For every odd prime ![]() $p$ (respectively
$p$ (respectively ![]() $p=\infty$),
$p=\infty$), ![]() ${\it\pi}_{p}$ is nontempered (respectively tempered). If we further assume that
${\it\pi}_{p}$ is nontempered (respectively tempered). If we further assume that ![]() $f$ is a new form,
$f$ is a new form, ![]() ${\it\pi}_{p}$ is nontempered for every finite prime
${\it\pi}_{p}$ is nontempered for every finite prime ![]() $p$ and tempered for
$p$ and tempered for ![]() $p=\infty$.
$p=\infty$.
Proof. The temperedness of ![]() ${\it\pi}_{\infty }$ is due to Proposition 6.5 and [Reference Collingwood6, Remark 2.1.13]. For an odd prime
${\it\pi}_{\infty }$ is due to Proposition 6.5 and [Reference Collingwood6, Remark 2.1.13]. For an odd prime ![]() $p$, the unramified characters
$p$, the unramified characters ![]() ${\it\chi}_{i}$ with
${\it\chi}_{i}$ with 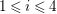 $1\leqslant i\leqslant 4$ are not unitary (cf. (6.6)). This means that
$1\leqslant i\leqslant 4$ are not unitary (cf. (6.6)). This means that ![]() ${\it\pi}_{p}$ is nontempered (cf. [Reference Sarnak27, (9)]).
${\it\pi}_{p}$ is nontempered (cf. [Reference Sarnak27, (9)]).
Let ![]() $p=2$, and suppose that
$p=2$, and suppose that ![]() $f$ is a new form. We recall that
$f$ is a new form. We recall that ![]() $f_{0}$ denotes the spherical vector in
$f_{0}$ denotes the spherical vector in ![]() ${\it\pi}_{2}$, and introduce its dual vector
${\it\pi}_{2}$, and introduce its dual vector ![]() $f_{0}^{\prime }$ in the contragredient representation of
$f_{0}^{\prime }$ in the contragredient representation of ![]() ${\it\pi}_{2}$. With the invariant measure
${\it\pi}_{2}$. With the invariant measure ![]() $dg$ of
$dg$ of ![]() ${\mathcal{G}}_{p}/Z_{p}$ normalized so that
${\mathcal{G}}_{p}/Z_{p}$ normalized so that  $\int _{K_{2}/Z_{p}}dg=1$, for any
$\int _{K_{2}/Z_{p}}dg=1$, for any ![]() ${\it\delta}>0$, we consider the following integral of the matrix coefficient:
${\it\delta}>0$, we consider the following integral of the matrix coefficient:
 $$\begin{eqnarray}\displaystyle \int _{{\mathcal{G}}_{2}/Z_{2}}|\langle {\it\pi}_{2}(g)f_{0},f_{0}^{\prime }\rangle |^{2+{\it\delta}}dg\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{{\mathcal{G}}_{2}/Z_{2}}|\langle {\it\pi}_{2}(g)f_{0},f_{0}^{\prime }\rangle |^{2+{\it\delta}}dg\end{eqnarray}$$ over ![]() ${\mathcal{G}}_{2}$ modulo center
${\mathcal{G}}_{2}$ modulo center ![]() $Z_{2}$, where
$Z_{2}$, where ![]() $\langle \ast ,\ast \rangle$ denotes the canonical pairing of
$\langle \ast ,\ast \rangle$ denotes the canonical pairing of ![]() ${\it\pi}_{2}$ and its contragredient. If
${\it\pi}_{2}$ and its contragredient. If ![]() ${\it\pi}_{2}$ is tempered, this integral should be convergent. Now we note that the set
${\it\pi}_{2}$ is tempered, this integral should be convergent. Now we note that the set 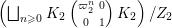 $\left(\sqcup _{n\geqslant 0}K_{2}\left(\!\begin{smallmatrix}{\it\varpi}_{2}^{n} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right)K_{2}\right)/Z_{2}$ can be regarded as a subdomain of
$\left(\sqcup _{n\geqslant 0}K_{2}\left(\!\begin{smallmatrix}{\it\varpi}_{2}^{n} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right)K_{2}\right)/Z_{2}$ can be regarded as a subdomain of ![]() ${\mathcal{G}}_{2}/Z_{2}$ and that there is a decomposition
${\mathcal{G}}_{2}/Z_{2}$ and that there is a decomposition
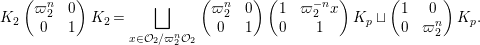 $$\begin{eqnarray}K_{2}\left(\begin{array}{@{}cc@{}}{\it\varpi}_{2}^{n} & 0\\ 0 & 1\end{array}\right)K_{2}=\underset{x\in {\mathcal{O}}_{2}/{\it\varpi}_{2}^{n}{\mathcal{O}}_{2}}{\sqcup }\left(\begin{array}{@{}cc@{}}\mathop{{\it\varpi}}_{2}^{n} & 0\\ 0 & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}1 & \mathop{{\it\varpi}}_{2}^{-n}x\\ 0 & 1\end{array}\right)K_{p}\sqcup \left(\begin{array}{@{}cc@{}}1 & 0\\ 0 & {\it\varpi}_{2}^{n}\end{array}\right)K_{p}.\end{eqnarray}$$
$$\begin{eqnarray}K_{2}\left(\begin{array}{@{}cc@{}}{\it\varpi}_{2}^{n} & 0\\ 0 & 1\end{array}\right)K_{2}=\underset{x\in {\mathcal{O}}_{2}/{\it\varpi}_{2}^{n}{\mathcal{O}}_{2}}{\sqcup }\left(\begin{array}{@{}cc@{}}\mathop{{\it\varpi}}_{2}^{n} & 0\\ 0 & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}1 & \mathop{{\it\varpi}}_{2}^{-n}x\\ 0 & 1\end{array}\right)K_{p}\sqcup \left(\begin{array}{@{}cc@{}}1 & 0\\ 0 & {\it\varpi}_{2}^{n}\end{array}\right)K_{p}.\end{eqnarray}$$ It is verified that the Hecke operator defined by  $K_{2}\left(\!\begin{smallmatrix}{\it\varpi}_{2}^{n} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right)K_{2}$ acts on
$K_{2}\left(\!\begin{smallmatrix}{\it\varpi}_{2}^{n} & 0\phantom{}\\ 0 & 1\end{smallmatrix}\!\right)K_{2}$ acts on ![]() $f_{0}$ as follows:
$f_{0}$ as follows:
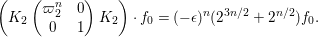 $$\begin{eqnarray}\left(K_{2}\left(\begin{array}{@{}cc@{}}{\it\varpi}_{2}^{n} & 0\\ 0 & 1\end{array}\right)K_{2}\right)\cdot f_{0}=(-{\it\epsilon})^{n}(2^{3n/2}+2^{n/2})f_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\left(K_{2}\left(\begin{array}{@{}cc@{}}{\it\varpi}_{2}^{n} & 0\\ 0 & 1\end{array}\right)K_{2}\right)\cdot f_{0}=(-{\it\epsilon})^{n}(2^{3n/2}+2^{n/2})f_{0}.\end{eqnarray}$$We thereby have a divergent integral
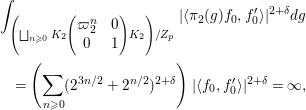 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{\left(\mathop{\sqcup }_{n\geqslant 0}K_{2}\left(\begin{array}{@{}cc@{}}{\it\varpi}_{2}^{n} & 0\\ 0 & 1\end{array}\right)K_{2}\right)/Z_{p}}|\langle {\it\pi}_{2}(g)f_{0},f_{0}^{\prime }\rangle |^{2+{\it\delta}}dg\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\displaystyle \mathop{\sum }_{n\geqslant 0}(2^{3n/2}+2^{n/2})^{2+{\it\delta}}\right)|\langle f_{0},f_{0}^{\prime }\rangle |^{2+{\it\delta}}=\infty ,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{\left(\mathop{\sqcup }_{n\geqslant 0}K_{2}\left(\begin{array}{@{}cc@{}}{\it\varpi}_{2}^{n} & 0\\ 0 & 1\end{array}\right)K_{2}\right)/Z_{p}}|\langle {\it\pi}_{2}(g)f_{0},f_{0}^{\prime }\rangle |^{2+{\it\delta}}dg\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\displaystyle \mathop{\sum }_{n\geqslant 0}(2^{3n/2}+2^{n/2})^{2+{\it\delta}}\right)|\langle f_{0},f_{0}^{\prime }\rangle |^{2+{\it\delta}}=\infty ,\nonumber\end{eqnarray}$$ which leads to a contradiction. We therefore see that ![]() ${\it\pi}_{2}$ is nontempered. As a result we are done.◻
${\it\pi}_{2}$ is nontempered. As a result we are done.◻
(1) According to Tadić [Reference Tadić28], the parabolic induction
 $I({\it\chi})$ for
$I({\it\chi})$ for  $p=2$ (cf. Section 6.1) has two composition factors, one of which is a unique essentially square integrable subquotient. Our nontempered representation
$p=2$ (cf. Section 6.1) has two composition factors, one of which is a unique essentially square integrable subquotient. Our nontempered representation  ${\it\pi}_{2}$ is the remaining nonsquare integrable composition factor. Besides our approach, there seem to be several ways to prove that the nonsquare integrable composition factor is nontempered. In fact, Tadić pointed out that the nontemperedness is proved by using the classification of the nonunitary dual of
${\it\pi}_{2}$ is the remaining nonsquare integrable composition factor. Besides our approach, there seem to be several ways to prove that the nonsquare integrable composition factor is nontempered. In fact, Tadić pointed out that the nontemperedness is proved by using the classification of the nonunitary dual of  $\text{GL}(n)$ over a division algebra (cf. [Reference Tadić28]) or by Casselman’s criterion on the temperedness of an admissible representation.
$\text{GL}(n)$ over a division algebra (cf. [Reference Tadić28]) or by Casselman’s criterion on the temperedness of an admissible representation.(2) From Weyl’s law (cf. [Reference Iwaniec12, (11.5)]), we can deduce that there exist nonzero new forms in
 $S({\rm\Gamma}_{0}(2);-(r^{2}/4+\frac{1}{4}))$ for some
$S({\rm\Gamma}_{0}(2);-(r^{2}/4+\frac{1}{4}))$ for some  $r\in \mathbb{R}$. Let
$r\in \mathbb{R}$. Let  $N_{{\rm\Gamma}}(T)$ be the counting function of an orthogonal basis of the discrete spectrum for a congruence subgroup
$N_{{\rm\Gamma}}(T)$ be the counting function of an orthogonal basis of the discrete spectrum for a congruence subgroup  ${\rm\Gamma}$, as in [Reference Iwaniec12, §11.1]. Put
${\rm\Gamma}$, as in [Reference Iwaniec12, §11.1]. Put  $N_{{\rm\Gamma}_{0}(2)}^{\ast }(T)$ to be such a counting function for new forms of
$N_{{\rm\Gamma}_{0}(2)}^{\ast }(T)$ to be such a counting function for new forms of  ${\rm\Gamma}_{0}(2)$. With the help of Casselman’s local theory of old forms and new forms (cf. [Reference Casselman5]), we deduce from Weyl’s law just mentioned. In view of Theorems 4.4 and 6.8, this leads to the existence of a nonzero cuspidal representation
${\rm\Gamma}_{0}(2)$. With the help of Casselman’s local theory of old forms and new forms (cf. [Reference Casselman5]), we deduce from Weyl’s law just mentioned. In view of Theorems 4.4 and 6.8, this leads to the existence of a nonzero cuspidal representation $$\begin{eqnarray}\displaystyle N_{{\rm\Gamma}_{0}(2)}^{\ast }(T) & = & \displaystyle \displaystyle \frac{\text{Vol}(\mathfrak{h}/{\rm\Gamma}_{0}(2))-2\text{Vol}(\mathfrak{h}/SL_{2}(\mathbb{Z}))}{4{\it\pi}}T^{2}+O(T\log T)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{\text{Vol}(\mathfrak{h}/SL_{2}(\mathbb{Z}))}{4{\it\pi}}T^{2}+O(T\log T)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{{\rm\Gamma}_{0}(2)}^{\ast }(T) & = & \displaystyle \displaystyle \frac{\text{Vol}(\mathfrak{h}/{\rm\Gamma}_{0}(2))-2\text{Vol}(\mathfrak{h}/SL_{2}(\mathbb{Z}))}{4{\it\pi}}T^{2}+O(T\log T)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \frac{\text{Vol}(\mathfrak{h}/SL_{2}(\mathbb{Z}))}{4{\it\pi}}T^{2}+O(T\log T)\nonumber\end{eqnarray}$$ ${\it\pi}_{F}$ whose local component
${\it\pi}_{F}$ whose local component  ${\it\pi}_{p}$ is nontempered at every
${\it\pi}_{p}$ is nontempered at every  $p<\infty$. We remark that the formula for
$p<\infty$. We remark that the formula for  $N_{{\rm\Gamma}_{0}(2)}^{\ast }(T)$ can be generalized to the case of any prime level.
$N_{{\rm\Gamma}_{0}(2)}^{\ast }(T)$ can be generalized to the case of any prime level.
Acknowledgments
From Masao Tsuzuki we have learned Weyl’s law for new Maass cusp forms for ![]() ${\rm\Gamma}_{0}(2)$, which leads to the existence of a nonzero cuspidal representation
${\rm\Gamma}_{0}(2)$, which leads to the existence of a nonzero cuspidal representation 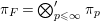 ${\it\pi}_{F}=\otimes _{p\leqslant \infty }^{\prime }{\it\pi}_{p}$ with nontempered local components
${\it\pi}_{F}=\otimes _{p\leqslant \infty }^{\prime }{\it\pi}_{p}$ with nontempered local components ![]() ${\it\pi}_{p}$ at every
${\it\pi}_{p}$ at every ![]() $p<\infty$. Marko Tadić kindly made his remark on the proof of the nontemperedness of
$p<\infty$. Marko Tadić kindly made his remark on the proof of the nontemperedness of ![]() ${\it\pi}_{2}$. These are summarized as Remark 6.9 above. Our deep gratitude is due to them. We would like to thank A. Raghuram for informing us of the paper [Reference Grobner9] by Grobner. Our thanks are also due to Harald Grobner for his comment on this paper. We would also like to thank Abhishek Saha for several discussions leading to the proof of the nonvanishing of the lifting. We finally express our profound gratitude to the referee for careful reading and fruitful comments.
${\it\pi}_{2}$. These are summarized as Remark 6.9 above. Our deep gratitude is due to them. We would like to thank A. Raghuram for informing us of the paper [Reference Grobner9] by Grobner. Our thanks are also due to Harald Grobner for his comment on this paper. We would also like to thank Abhishek Saha for several discussions leading to the proof of the nonvanishing of the lifting. We finally express our profound gratitude to the referee for careful reading and fruitful comments.