Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T23:38:19.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Level 0 Monomial Crystals

Published online by Cambridge University Press:  11 January 2016

David Hernandez  and
Hiraku Nakajima
David Hernandez
Affiliation:
CNRS - UMR 8100: Laboratoire de Mathématiques de Versailles45 avenue des Etats-Unis, Bat. Fermat, 78035 [email protected]
Hiraku Nakajima
Affiliation:
Department of MathematicsKyoto UniversityKyoto, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

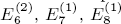We study the monomial crystal defined by the second author. We show that each component of the monomial crystal can be embedded into a crystal of an extremal weight module introduced by Kashiwara. And we determine all monomials appearing in the components corresponding to all level 0 fundamental representations of quantum affine algebras except for some nodes of . Thus we obtain explicit descriptions of the crystals in these examples. We also give those for the corresponding finite dimensional representations. For classical types, we give them in terms of tableaux. For exceptional types, we list up all monomials.

Keywords

17B3717B65
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 184 , 2006 , pp. 85 - 153
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2006

References

[1] Akasaka, T. and Kashiwara, M., Finite dimensional representations of quantum affine algebras, Publ. Res. Inst. Math. Sci., 33 (1997), no. 5, 839–867.CrossRefGoogle Scholar
[2] Beck, J., Crystal structure of level zero extremal weight modules, Lett. Math. Phys., 61 (2002), no. 3, 221–229.CrossRefGoogle Scholar
[3] Benkart, G. Frenkel, I., Kang, S. J. and Lee, H., Level 1 perfect crystals and path realizations of basic representations at q = 0, preprint, math.RT/0507114.Google Scholar
[4] Beck, J. and Nakajima, H., Crystal bases and two-sided cells of quantum affine algebras, Duke Math. J., 123 (2004), no. 2, 335–402.CrossRefGoogle Scholar
[5] Chari, V. and Moura, A., Characters and blocks for finite-dimensional representations of quantum affine algebras, Int. Math. Res. Not. 2005, no. 5, 257–298.CrossRefGoogle Scholar
[6] Frenkel, E. and Mukhin, E., Combinatorics of q-characters of finite-dimensional representations of quantum affine algebras, Comm. Math. Phy., 216 (2001), no. 1, 23–57.CrossRefGoogle Scholar
[7] Frenkel, E. and Reshetikhin, N., The q-characters of representations of quantum affine algebras and deformations of W-algebras, Recent Developments in Quantum Affine Algebras and related topics, Cont. Math., vol. 248 (1999), pp. 163–205.CrossRefGoogle Scholar
[8] Hernandez, D., Algebraic approach to q,t-characters, Adv. Math., 187 (2004), no. 1, 1–52.CrossRefGoogle Scholar
[9] Hernandez, D., Representations of quantum affinizations and fusion product, Trans-for. Groups, 10 (2005), no. 2, 163–200.CrossRefGoogle Scholar
[10] Hernandez, D., Monomials of q and q,t-chraracters for non simply-laced quantum affinizations, Math. Z., 250 (2005), no. 2, 443–473.CrossRefGoogle Scholar
[11] Jing, N. and Misra, K. C., Vertex operators for twisted quantum affine algebras, Trans. Amer. Math. Soc., 351 (1999), no. 4, 1663–1690.CrossRefGoogle Scholar
[12] Jing, N., Misra, K. C. and Okado, M., q-wedge modules for quantized enveloping algebras of classical type, J. Algebra, 230 (2000), 518–539.CrossRefGoogle Scholar
[13] Kac, V., Infinite dimensional Lie algebras, 3rd Edition, Cambridge University Press, 1990.CrossRefGoogle Scholar
[14] Kang, M. Kashiwara, S. J., Misra, K. C. Miwa, T., Nakashima, T. and Nakayashiki, A., Affine crystals and vertex models, Proceeding of the RIMS Research Project 1991 “Infinite Analysis”, International Journal of Modern Physics A 7, Suppl. 1A (1992), 449–484.CrossRefGoogle Scholar
[15] Kang, S. J., Kim, J. A. and Shin, D. U., Crystal bases of quantum classical algebras and Nakajima’s monomials, Publ. RIMS, Kyoto Univ., 40 (2004), 757–791.Google Scholar
[16] Kang, S. J. and Misra, K. C., Crystal bases and tensor product decompositions of Uq(G2)-modules, J. Algebra, 163 (1994), no. 3, 675–691.CrossRefGoogle Scholar
[17] Kashiwara, M., The crystal base and Littelmann’s refine Demazure character formula, Duke Math. J., 71 (1993), 839–858.CrossRefGoogle Scholar
[18] Kashiwara, M., Crystal bases of modified quantized enveloping algebra, Duke Math. J., 73 (1994), no. 2, 383–413.CrossRefGoogle Scholar
[19] Kashiwara, M., On level-zero representation of quantized affine algebras, Duke Math. J., 112 (2002), no. 1, 117–175.CrossRefGoogle Scholar
[20] Kashiwara, M., Bases cristallines des groupes quantiques, noted by C. Cochet, Cours Spéecialisées 9, Sociéetée Mathéematique de France, Paris, 2002.Google Scholar
[21] Kashiwara, M., Realizations of crystals, Combinatorial and geometric representation theory (Seoul, 2001), Contemp. Math., 325, Amer. Math. Soc., Providence, RI (2003), pp. 133–139.Google Scholar
[22] Kashiwara, M., Level zero fundamental representations over quantized affine algebras and Demazure modules, Publ. Res. Inst. Math. Sci., 41 (2005), no. 1, 223–250.CrossRefGoogle Scholar
[23] Kashiwara, M. and Nakashima, T., Crystal graphs for representations of the q-ana-logue of classical Lie algebras, J. Algebra, 165 (1994), 295–345.CrossRefGoogle Scholar
[24] Koga, Y., Level one perfect crystals for , J. Alg., 217 (1999), 312–334.CrossRefGoogle Scholar
[25] Knight, H., Spectra of tensor products of finite-dimensional representations of Yan-gians, J. Algebra, 174 (1995), no. 1, 187–196.CrossRefGoogle Scholar
[26] Kuniba, A. Okado, M., Suzuki, J, and Yamada, Y., Difference L operators related to q-characters, J. Phys. A, 35 (2002), no. 6, 1415–1435.CrossRefGoogle Scholar
[27] Magyar, P., Littelmann paths for the basic representation of an affine Lie algebra, preprint, math.RT/0308156.Google Scholar
[28] Nakajima, H., Quiver varieties and finite-dimensional representations of quantum affine algebras, J. Amer. Math. Soc., 14 (2001), no. 1, 145–238.CrossRefGoogle Scholar
[29] Nakajima, H., T-analogue of the q-characters of finite dimensional representations of quantum affine algebras, Physics and combinatorics, 2000 (Nagoya), World Sci. Publishing, River Edge, NJ (2001), pp. 196–219.Google Scholar
[30] Nakajima, H., Quiver varieties and tensor products, Invent. Math., 146 (2001), 399–449.CrossRefGoogle Scholar
[31] Nakajima, H., Quiver varieties and t-analogs of q-characters of quantum affine algebras, Ann. of Math., 160 (2004), 1057–1097.CrossRefGoogle Scholar
[32] Nakajima, H., t-analogs of q-characters of quantum affine algebras of type An, Dn, Combinatorial and geometric representation theory (Seoul, 2001), Contemp. Math., 325, Amer. Math. Soc., Providence, RI (2003), pp. 141–160.Google Scholar
[33] Nakajima, H., Extremal weight modules of quantum affine algebras, Advances Studies in Pure Math., 40 (2004), 343–369.CrossRefGoogle Scholar
[34] Naito, S. and Sagaki, D., Path model for a level-zero extremal weight module over a quantum affine algebra, Int. Math. Res. Not. 2003 (2003), no. 32, 1731–1754.Google Scholar
[35] Naito, S. and Sagaki, D., Path model for a level-zero extremal weight module over a quantum affine algebra II, Adv. Math., 200 (2006), no. 1, 102–124.CrossRefGoogle Scholar
[36] Okado, M., Schilling, A. and Shimozono, M., Virtual crystals and fermionic formulas of type and , Represent. Theory, 7 (2003), 101–163.CrossRefGoogle Scholar
[37] Schilling, A., A bijection between type crystals and rigged configurations, J. Algebra, 285 (2005), no. 1, 292–334.CrossRefGoogle Scholar
[38] Yamane, S., Perfect crystals of , J. Algebra, 210 (1998), no. 2, 440–486.Google Scholar