Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Miyake, Katsuya
1991.
The arithmetic structure of the Galois group of the maximal nilpotent extension of an algebraic number field.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 67,
Issue. 2,
Opolka, Hans
2007.
A Note on Regular Crossed Products and Galois Representations.
Communications in Algebra,
Vol. 35,
Issue. 5,
p.
1469.


 (
(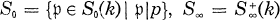 and
and 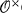 (
(