Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ono, Hiroakira
1986.
Craig's interpolation theorem for the intuitionistic logic and its extensions—A semantical approach.
Studia Logica,
Vol. 45,
Issue. 1,
p.
19.


 →
→ 
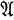 and
and