Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T23:52:53.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Le principe semi-complet du maximum pour les noyaux de convolution réels

Published online by Cambridge University Press:  22 January 2016

Masayuki Itô
Masayuki Itô*
Affiliation:
Département de Mathématiques, Faculté des Sciences, Université de Nagoya Nagoya 464, Japon
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit X un groupe abélien localement compact, non-compact, séparé et dénombrable à l’infini. On désignera par ξ une mesure de Haar fixée sur X. Pour les noyaux de convolution réels sur X, le principe semi-complet du maximum est fondamental dans la théorie du potentiel. Soit N un noyau de convolution réel sur X vérifiant le principe semi-complet du maximum (désigné par Nє(PSM)). Pour déterminer l’allure de N à l’infini, la N-réduite ηN, δ de N à l’infini δ joue un rôle essentiel. Pour une exhaustion 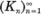de compacts de 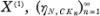est décroissante et 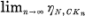est une mesure de Radon réelle sur X ou bien, pour une fonction 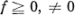finie et continue dans X à support compact quelconque, 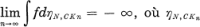est la iV-réduite de N sur CKn. Dans ce cas, 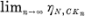est indépendant du choix de 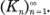Posons

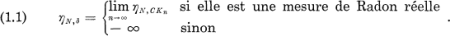
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 101 , March 1986 , pp. 55 - 109
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1986

References

Bibliographie

[ 1 ] Berg, C. et Forst, G., Potential theory on locally compact abeliean groups, Springer-Verlag, Berlin-Heidelberg-Newyork, 1975.CrossRefGoogle Scholar
[ 2 ] Choquet, G. et Deny, J., Sur l’équation de convolution μ = μ*σ , C. R. Acad., Sci. Paris, 250 (1960), 799–801.Google Scholar
[ 3 ] Deny, J., Noyaux de convolution de Hunt et noyaux associés à une famille fondamentale, Ann. Inst. Fourier, 12 (1962), 643–667.CrossRefGoogle Scholar
[ 4 ] Itô, M., Caractérisation du principe de domination pour les noyaux de convolution non-bornés, Nagoya Math. J., 57 (1975), 167–197.CrossRefGoogle Scholar
[ 5 ] Itô, M., Sur le principe de domination relatif, le balayage et les noyaux conditionnellement sous-médians, J. Math, pures appl., 57 (1978), 423–451.Google Scholar
[ 6 ] Itô, M., Positive eigen elements for an infinitesimal generator of a diffusion semi group and their integral representations, Proceeding Potential theory, Copenhagen 1979, Lecture Note in Math., 787 (1979), 163–183, Springer-Verlag.Google Scholar
[ 7 ] Itô, M., Une caractérisation des noyaux de convolution réels de type logarithmique, Nagoya Math. J., 97 (1985), 1–49.Google Scholar
[ 8 ] Itô, M. et Suzuki, N., The semi-balayability of real convolution kernels, Nagoya Math. J., 99 (1985), 89–110.CrossRefGoogle Scholar
[ 9 ] Phelps, R. R., Lectures on Choquet’s theorem, Van Nostrand Math. Studies #7, Princeton, 1965.Google Scholar
[10] Stanpacchia, G., Formes bilinéaires coercitives sur les ensembles convexes, C. R. Acad. Sci. Paris, 258 (1964), 4413–4416.Google Scholar
[11] Stanpacchia, G., Le problème de Dirichlet pour les équation elliptiques du second ordre à coefficients discontinus, Ann. Inst. Fourier, 15 (1965), 189–256.CrossRefGoogle Scholar
[12] Weil, A., L’intégration dans les groupes topologiques et ses applications, Hermann, Paris, 1965.Google Scholar