Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-25T07:05:51.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Le Groupe GLn Tordu, Sur un Corps Fini

Published online by Cambridge University Press:  11 January 2016

J.-L. Waldspurger
J.-L. Waldspurger*
Affiliation:
CNRS-Institut de Mathématiques de Jussieu, 175, rue du Chevaleret 75013 Paris, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 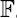q be a finite field, G = GLn(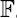q), θ be the outer automorphism of G, suitably normalized. Consider the non-connected group G ⋊ {1, θ} and its connected component = Gθ. We know two ways to produce functions on , with complex values and invariant by conjugation by G: on one hand, let π be an irreducible representation of G we can and do extend to a representation π+ of G ⋊ {1, θ}, then the restriction trace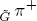 to of the character of π+ is such a function; on the other hand, Lusztig define character-sheaves a, whose characteristic functions ϕ(a) are such functions too. We consider only “quadratic-unipotent” representations. For all such representation π, we define a suitable extension π+, a character-sheave f(π) and we prove an identity trace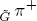 = γ(π)ϕ(f(π)) with an explicit complex number γ(π).

Keywords

20C3320G40
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 182: Special Issue Celebrating the 60th Birthday of George Lusztig , June 2006 , pp. 313 - 379
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2006

References

Bibliographie

[A] Asai, T., Unipotent class functions of split special orthogonal groups SO+n over finite fields, Comm. Algebra, 12 (1984), 517–615.CrossRefGoogle Scholar
[AMR] Aubert, A.-M., Michel, J. and Rouquier, R., Correspondance de Howe pour les groupes réductifs sur les corps finis, Duke Math. J., 83 (1996), 353–397.Google Scholar
[CR] Curtis, C. and Reiner, I., Methods of representation theory, with applications to finite groups and orders, vol. 1, Wiley Interscience, 1981.Google Scholar
[DM] Digne, F. and Michel, J., Groupes réductifs non connexes, Ann. Scient. ENS, 27 (1994), 345–406.Google Scholar
[L1] Lusztig, G., Character sheaves V, Adv. in Math., 61 (1986), 103–165.CrossRefGoogle Scholar
[L2] Lusztig, G., Character sheaves on disconnected groups III, Representation Th., 8 (2004), 125–154.CrossRefGoogle Scholar
[L3] Lusztig, G., Character sheaves on disconnected groups IV, Representation Th., 8 (2004), 155–188.Google Scholar
[L4] Lusztig, G., Character sheaves on disconnected groups V, Representation Th., 8 (2004), 346–376.Google Scholar
[L5] Lusztig, G., Green functions and character sheaves, Annals of Math., 131 (1990), 355–408.CrossRefGoogle Scholar
[S] Spaltenstein, N., Classes unipotentes et sous-groupes de Borel, Springer L.N. 946, 1980.Google Scholar
[W1] Waldspurger, J.-L., Une conjecture de Lusztig pour les groupes classiques, Mémoires SMF 96, 2004.Google Scholar
[W2] Waldspurger, J.-L., Intégrales orbitales nilpotentes et endoscopie pour les groupes classiques non ramifiés, Astérisque 269, 2001.Google Scholar