Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Khoshnevisan, Davar
and
Shi, Zhan
2000.
Séminaire de Probabilités XXXIV.
Vol. 1729,
Issue. ,
p.
393.
Khoshnevisan, Davar
Peres, Yuval
and
Xiao, Yimin
2000.
Limsup Random Fractals.
Electronic Journal of Probability,
Vol. 5,
Issue. none,
Khoshnevisan, Davar
and
Xiao, Yimin
2004.
Fractal Geometry and Stochastics III.
p.
151.
Fouché, Willem L.
2008.
Dynamics of a generic Brownian motion: Recursive aspects.
Theoretical Computer Science,
Vol. 394,
Issue. 3,
p.
175.
Potgieter, Paul
2012.
The rapid points of a complex oscillation.
Logical Methods in Computer Science,
Vol. Volume 8, Issue 1,
Issue. ,
Fouché, Willem L.
and
Mukeru, Safari
2013.
On the Fourier structure of the zero set of fractional Brownian motion.
Statistics & Probability Letters,
Vol. 83,
Issue. 2,
p.
459.
Xiao, Yimin
2013.
Further Developments in Fractals and Related Fields.
p.
255.
Potgieter, Paul
2015.
The Fourier dimension of Brownian limsup fractals.
Statistics & Probability Letters,
Vol. 106,
Issue. ,
p.
228.
Mukeru, Safari
2018.
The Zero Set of Fractional Brownian Motion Is a Salem Set.
Journal of Fourier Analysis and Applications,
Vol. 24,
Issue. 4,
p.
957.


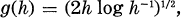 and let 0 <
and let 0 <