Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kang, Hyeonbae
and
Seo, Jin Keun
1995.
Cauchy transforms on polynomial curves and related operators.
Nagoya Mathematical Journal,
Vol. 138,
Issue. ,
p.
19.


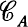 on the curve
on the curve 
