Published online by Cambridge University Press: 11 January 2016
Let (X, ω) be a weakly pseudoconvex Kähler manifold, Y ⊂ X a closed submanifold defined by some holomorphic section of a vector bundle over X, and L a Hermitian line bundle satisfying certain positivity conditions. We prove that for any integer k > 0, any section of the jet sheaf 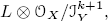 which satisfies a certain L2 condition, can be extended into a global holomorphic section of L over X whose L2 growth on an arbitrary compact subset of X is under control. In particular, if Y is merely a point, this gives the existence of a global holomorphic function with an L2 norm under control and with prescribed values for all its derivatives up to order k at that point. This result generalizes the L2 extension theorems of Ohsawa-Takegoshi and of Manivel to the case of jets of sections of a line bundle. A technical difficulty is to achieve uniformity in the constant appearing in the final estimate. To this end, we make use of the exponential map and of a Rauch-type comparison theorem for complete Riemannian manifolds.
which satisfies a certain L2 condition, can be extended into a global holomorphic section of L over X whose L2 growth on an arbitrary compact subset of X is under control. In particular, if Y is merely a point, this gives the existence of a global holomorphic function with an L2 norm under control and with prescribed values for all its derivatives up to order k at that point. This result generalizes the L2 extension theorems of Ohsawa-Takegoshi and of Manivel to the case of jets of sections of a line bundle. A technical difficulty is to achieve uniformity in the constant appearing in the final estimate. To this end, we make use of the exponential map and of a Rauch-type comparison theorem for complete Riemannian manifolds.