Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tu, Zhen-Han
1996.
On the Julia directions of the value distribution of holomorphic curves in ${\rm P}^n({\bf C})$.
Kodai Mathematical Journal,
Vol. 19,
Issue. 1,


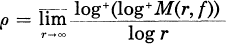
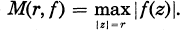 A ray
A ray 