Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
LOPES, MARGARIDA MENDES
and
PARDINI, RITA
2000.
TRIPLE CANONICAL SURFACES OF MINIMAL DEGREE.
International Journal of Mathematics,
Vol. 11,
Issue. 04,
p.
553.
Ciliberto, Ciro
Pardini, Rita
and
Tovena, Francesca
2003.
Regular canonical covers.
Mathematische Nachrichten,
Vol. 251,
Issue. 1,
p.
19.
Bin, Nguyen
2021.
Some infinite sequences of canonical covers of degree 2.
Advances in Geometry,
Vol. 21,
Issue. 1,
p.
143.
Mendes Lopes, Margarida
and
Pardini, Rita
2023.
The Art of Doing Algebraic Geometry.
p.
305.


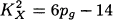 such that the canonical map is 2-to-l onto a canonically embedded surface.
such that the canonical map is 2-to-l onto a canonically embedded surface.