Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kaneta, Hitoshi
1982.
Irreducibility of some unitary representations of the Poincaré group with respect to the Poincaré subsemigroup, III.
Nagoya Mathematical Journal,
Vol. 87,
Issue. ,
p.
175.


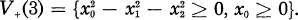 The multiplication is defined by the formula
The multiplication is defined by the formula