Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T05:12:02.851Z Has data issue: false hasContentIssue false
  • English
  • Français

INTERTWINING SEMISIMPLE CHARACTERS FOR 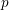$p$-ADIC CLASSICAL GROUPS

Part of: Forms and linear algebraic groups Lie groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  16 July 2018

DANIEL SKODLERACK  and
SHAUN STEVENS
DANIEL SKODLERACK
Affiliation:
School of Mathematics, University of East Anglia, Norwich Research Park, Norwich NR4 7TJ, UK email [email protected]
SHAUN STEVENS
Affiliation:
School of Mathematics, University of East Anglia, Norwich Research Park, Norwich NR4 7TJ, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 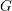$G$ be an orthogonal, symplectic or unitary group over a non-archimedean local field of odd residual characteristic. This paper concerns the study of the “wild part” of an irreducible smooth representation of 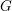$G$, encoded in its “semisimple character”. We prove two fundamental results concerning them, which are crucial steps toward a complete classification of the cuspidal representations of 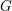$G$. First we introduce a geometric combinatorial condition under which we prove an “intertwining implies conjugacy” theorem for semisimple characters, both in 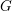$G$ and in the ambient general linear group. Second, we prove a Skolem–Noether theorem for the action of 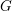$G$ on its Lie algebra; more precisely, two semisimple elements of the Lie algebra of 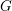$G$ which have the same characteristic polynomial must be conjugate under an element of 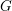$G$ if there are corresponding semisimple strata which are intertwined by an element of 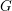$G$.

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Secondary: 11E57: Classical groups 11E95: $p$-adic theory 20G05: Representation theory
Type
Article
Information
Nagoya Mathematical Journal , Volume 238 , June 2020 , pp. 137 - 205
Copyright
© 2018 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was funded by EPSRC grant EP/H00534X/1.

References

Broussous, P. and Lemaire, B., Building of GL(m, D) and centralizers, Transform. Groups 7(1) (2002), 15–50.10.1007/BF01253463Google Scholar
Broussous, P., Sécherre, V. and Stevens, S., Smooth representations of GLm(D) V: endo-classes, Doc. Math. 17 (2012), 23–77.Google Scholar
Broussous, P. and Stevens, S., Buildings of classical groups and centralizers of Lie algebra elements, J. Lie Theory 19(1) (2009), 55–78.Google Scholar
Bruhat, F. and Tits, J., Schémas en groupes et immeubles des groupes classiques sur un corps local. II. Groupes unitaires, Bull. Soc. Math. France 115(2) (1987), 141–195.Google Scholar
Bushnell, C. J., Hereditary orders, Gauss sums and supercuspidal representations of GLN, J. Reine Angew. Math. 375/376 (1987), 184–210.Google Scholar
Bushnell, C. J. and Henniart, G., Local tame lifting for GL(N). I. Simple characters, Inst. Hautes Études Sci. Publ. Math. 83 (1996), 105–233.10.1007/BF02698646Google Scholar
Bushnell, C. J. and Henniart, G., Local tame lifting for GL(n). IV. Simple characters and base change, Proc. Lond. Math. Soc. (3) 87(2) (2003), 337–362.10.1112/S0024611503014114Google Scholar
Bushnell, C. J. and Henniart, G., Higher ramification and the local Langlands correspondence, Ann. of Math. (2) 185(3) (2017), 919–955.10.4007/annals.2017.185.3.5Google Scholar
Bushnell, C. J. and Kutzko, P. C., The Admissible Dual of GL(N) Via Compact Open Subgroups, Vol. 129, Princeton University Press, Princeton, NJ, 1993.Google Scholar
Bushnell, C. J. and Kutzko, P. C., “Simple types in GL(N): computing conjugacy classes”, in Representation Theory and Analysis on Homogeneous Spaces (New Brunswick, NJ, 1993), Contemp. Math. 177, Amer. Math. Soc., Providence, RI, 1994, 107–135.10.1090/conm/177/01918Google Scholar
Bushnell, C. J. and Kutzko, P. C., Semisimple types in GLn, Compos. Math. 119(1) (1999), 53–97.10.1023/A:1001773929735Google Scholar
Dat, J.-F., Finitude pour les représentations lisses de groupes p-adiques, J. Inst. Math. Jussieu 8(2) (2009), 261–333.10.1017/S1474748008000054Google Scholar
Kurinczuk, R., Skodlerack, D. and Stevens, S., Endoclasses for $p$-adic classical groups, preprint, 2016, arXiv:1611.02667.Google Scholar
Kurinczuk, R. and Stevens, S., Cuspidal $\ell$-modular representations of $p$-adic classical groups, preprint, 2015, arXiv:1509.02212.Google Scholar
Reiner, I., Maximal Orders, The Clarendon Press, Oxford University Press, Oxford, 2003.Google Scholar
Sécherre, V. and Stevens, S., Towards an explicit local Jacquet–Langlands correspondence beyond the cuspidal case, preprint, 2016, arXiv:1611.04317.Google Scholar
Skodlerack, D., Field embeddings which are conjugate under a p-adic classical group, Manuscripta Math. 144(1–2) (2014), 277–301.10.1007/s00229-013-0654-6Google Scholar
Skodlerack, D., Semisimple characters for inner forms I: $\text{GL}_{n}(D)$, preprint, 2017, arXiv:1703.04904.Google Scholar
Stevens, S., Double coset decompositions and intertwining, Manuscripta Math. 106(3) (2001), 349–364.10.1007/PL00005887Google Scholar
Stevens, S., Intertwining and supercuspidal types for p-adic classical groups, Proc. Lond. Math. Soc. (3) 83(1) (2001), 120–140.Google Scholar
Stevens, S., Semisimple strata for p-adic classical groups, Ann. Sci. Éc. Norm. Supér. (4) 35(3) (2002), 423–435.Google Scholar
Stevens, S., Semisimple characters for p-adic classical groups, Duke Math. J. 127(1) (2005), 123–173.10.1215/S0012-7094-04-12714-9Google Scholar
Stevens, S., The supercuspidal representations of p-adic classical groups, Invent. Math. 172(2) (2008), 289–352.10.1007/s00222-007-0099-1Google Scholar