Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T20:14:09.199Z Has data issue: false hasContentIssue false
  • English
  • Français

INTEGRAL CLOSURE OF STRONGLY GOLOD IDEALS

Part of: Commutative algebra: Homological methods General commutative ring theory Ring extensions and related topics

Published online by Cambridge University Press:  18 July 2019

CĂTĂLIN CIUPERCĂ Open the ORCID record for CĂTĂLIN CIUPERCĂ [Opens in a new window]
CĂTĂLIN CIUPERCĂ*
Affiliation:
Department of Mathematics 2750, North Dakota State University, PO BOX 6050, Fargo, ND 58108-6050, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the integral closure of a strongly Golod ideal in a polynomial ring over a field of characteristic zero is strongly Golod, positively answering a question of Huneke. More generally, the rational power 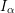$I_{\unicode[STIX]{x1D6FC}}$ of an arbitrary homogeneous ideal is strongly Golod for 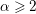$\unicode[STIX]{x1D6FC}\geqslant 2$ and, if 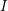$I$ is strongly Golod, then 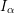$I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for 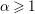$\unicode[STIX]{x1D6FC}\geqslant 1$. We also show that all the coefficient ideals of a strongly Golod ideal are strongly Golod.

MSC classification

Primary: 13A30: Associated graded rings of ideals (Rees ring, form ring), analytic spread and related topics 13B22: Integral closure of rings and ideals ; integrally closed rings, related rings (Japanese, etc.)
Secondary: 13D40: Hilbert-Samuel and Hilbert-Kunz functions; Poincaré series
Type
Article
Information
Nagoya Mathematical Journal , Volume 241 , March 2021 , pp. 204 - 216
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

De Stefani, A., Products of ideals may not be Golod, J. Pure Appl. Algebra 220(6) (2016), 2289–2306.10.1016/j.jpaa.2015.11.007Google Scholar
Heinzer, W. and Lantz, D., “Coefficient and stable ideals in polynomial rings”, in Factorization in Integral Domains (Iowa City, IA, 1996), Lecture Notes in Pure and Applied Mathematics 189, Dekker, New York, 1997, 359–370.Google Scholar
Herzog, J. and Huneke, C., Ordinary and symbolic powers are Golod, Adv. Math. 246 (2013), 89–99.10.1016/j.aim.2013.07.002Google Scholar
Huneke, C. and Swanson, I., Integral Closure of Ideals, Rings, and Modules, London Mathematical Society Lecture Note Series 336, Cambridge University Press, Cambridge, 2006.Google Scholar
Matsumura, H., Commutative Ring Theory, 2nd ed., Cambridge Studies in Advanced Mathematics 8, Cambridge University Press, Cambridge, 1989, Translated from the Japanese by M. Reid.Google Scholar
McCullough, J. and Peeva, I., “Infinite graded free resolutions”, in Commutative Algebra and Noncommutative Algebraic Geometry, Vol. I, Mathematical Science Research Institute Publications 67, Cambridge University Press, New York, 2015, 215–257.Google Scholar
Seidenberg, A., Derivations and integral closure, Pacific J. Math. 16 (1966), 167–173.10.2140/pjm.1966.16.167Google Scholar
Shah, K., Coefficient ideals, Trans. Amer. Math. Soc. 327(1) (1991), 373–384.10.1090/S0002-9947-1991-1013338-3Google Scholar