Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-06T10:42:10.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrability of the Backward Diffusion Equation in a Compact Riemannian Space

Published online by Cambridge University Press:  22 January 2016

Kôsaku Yosida
Kôsaku Yosida*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be an orientable, compact Riemannian space with the metric ds2=gij(x)dxidxj and consider the backward diffusion equation

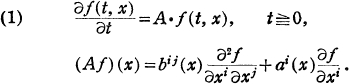
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 3 , October 1951 , pp. 1 - 4
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1951

References

1) Kolmogoroff, A.: Zur Théorie der stetigen zufälligen Prozesse, Math. Ann., 108 (1933), 149–160 CrossRefGoogle Scholar. Yosida, K.: An extension of Fokker-Planck’s equation, Proc. Japan Acad., 25 (1949), (9), 1–3.CrossRefGoogle Scholar

2) Yosida, K.: Integration of Fokker-Planck’s equation in a compact Riemannian space, Arkiv for Matematik, 1 (1949), 9, 71–75 CrossRefGoogle Scholar. Yosida, K.: Integration of Foker-Planck’s equation with boundary condition, Journ. Math. Soc. Japan, (1951)CrossRefGoogle Scholar, Takagi’s Congratulation volumec

3) Hille, E.: Functional Analysis and Semi-groups, New York (1948)Google Scholar. Yosida, K.: On the differentiability and the representation of one-parameter semi-group of linear operators, Journ. Math. Soc. Japan, 1 (1949), 1, 15–21 Google Scholar, and Yosida, K.: An operator-theoretical treatment of temporally homogeneous Markoff process, ibid., 1 (1949), 1, 224–235.Google Scholar

4) Cf. another approach by Itô, K.: Stochastic differentiable equations on a differentiate manifold, Nagoya Math. J., 1 (1950), 35–48.CrossRefGoogle Scholar

5 By the topology defined by the norm ‖f‖, viz. by the uniform convergence on R.

6) Schwartz, L.: Théorie des distributions, 1, Paris (1950).Google Scholar

7) L. Schwartz: loc. cif., p. 136,