Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lawson, Terry
1985.
Normal bundles for an embedded $\mathrm{R}p^2$ in a positive definite 4-manifold.
Journal of Differential Geometry,
Vol. 22,
Issue. 2,
Fintushel, Ronald
and
Stern, Ronald
1987.
Rational homology cobordisms of spherical space forms.
Topology,
Vol. 26,
Issue. 3,
p.
385.
Ruberman, Daniel
1988.
Rational homology cobordisms of rational space forms.
Topology,
Vol. 27,
Issue. 4,
p.
401.
Nakajima, Hiraku
1990.
Recent Topics in Differential and Analytic Geometry.
p.
385.
Bando, Shigetoshi
1990.
Kähler Metric and Moduli Spaces.
p.
105.
Furuta, Mikio
1990.
Homology cobordism group of homology 3-spheres.
Inventiones Mathematicae,
Vol. 100,
Issue. 1,
p.
339.
Boden, Hans U.
1991.
Representations of orbifold groups and parabolic bundles.
Commentarii Mathematici Helvetici,
Vol. 66,
Issue. 1,
p.
389.
1992.
A note on
K
-theoretical index theorems for orbifolds
.
Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences,
Vol. 437,
Issue. 1900,
p.
429.
Furuta, Mikio
1992.
On self-dual pseudo-connections on some orbifolds.
Mathematische Zeitschrift,
Vol. 209,
Issue. 1,
p.
319.
Ouyang, Ming Qing
1994.
Geometric invariants for Seifert fibred 3-manifolds.
Transactions of the American Mathematical Society,
Vol. 346,
Issue. 2,
p.
641.
Hodgkin, Luke
1995.
The complex structure of supermoduli space.
Classical and Quantum Gravity,
Vol. 12,
Issue. 9,
p.
2135.
Vergne, Michele
1996.
Equivariant index formulas for orbifolds.
Duke Mathematical Journal,
Vol. 82,
Issue. 3,
Jeffrey, Lisa C.
and
Kirwan, Frances C.
1997.
Localization and the quantization conjecture.
Topology,
Vol. 36,
Issue. 3,
p.
647.
MARCOLLI, MATILDE
and
MATHAI, VARGHESE
1999.
TWISTED INDEX THEORY ON GOOD ORBIFOLDS, I: NONCOMMUTATIVE BLOCH THEORY.
Communications in Contemporary Mathematics,
Vol. 01,
Issue. 04,
p.
553.
Greene, B.R.
Lazaroiu, C.I.
and
Yi, Piljin
1999.
D-particles on T/ orbifolds and their resolutions.
Nuclear Physics B,
Vol. 539,
Issue. 1-2,
p.
135.
Crainic, Marius
and
Moerdijk, Ieke
2000.
A homology theory for étale groupoids.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2000,
Issue. 521,
Ue, Masaaki
2001.
On the intersection forms of spin 4–manifolds bounded by spherical 3–manifolds.
Algebraic & Geometric Topology,
Vol. 1,
Issue. 1,
p.
549.
Acosta, Daniel J.
2001.
A Furuta-like inequality for spin orbifolds and the minimal genus problem.
Topology and its Applications,
Vol. 114,
Issue. 1,
p.
91.
Fukumoto, Yoshihiro
Furuta, Mikio
and
Ue, Masaaki
2001.
W-invariants and Neumann–Siebenmann invariants for Seifert homology 3-spheres.
Topology and its Applications,
Vol. 116,
Issue. 3,
p.
333.
Paradan, Paul-Emile
2001.
Localization of the Riemann–Roch Character.
Journal of Functional Analysis,
Vol. 187,
Issue. 2,
p.
442.


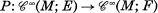 be a
be a 