Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T16:13:40.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Ideals of bounded holomorphic functions on simple n-sheeted discs

Published online by Cambridge University Press:  22 January 2016

Masaru Hara
Masaru Hara*
Affiliation:
Department of Mathematics, Meijo University, Shiogamaguchi, Tenpaku, Nagoya 468, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

As usual we denote by H∞(K) the Banach algebra of bounded holomorphic functions on a Riemann surface R equipped with the supremum norm ‖·‖ Consider the ideal I(f1 … fm) of H∞(R) generated by functions f1 …fm in H∞(R). If a function g in H∞(R) belongs to I(f1 … fm or equivalently, if there exist m functions h1 …, hm in H∞(R) with

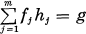
on R, then common zero points of f1, ... fm are also zero points of g in the following strong sense:

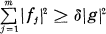
on R for a positive constant δ > 0. The generalized corona problem asks whether the converse is valid or not. In the case g ≡ 1 on R the problem is referred to simply as the corona problem.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 123 , September 1991 , pp. 171 - 201
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1991

References

[A1] Ailing, N., A proof of the corona conjecture for finite open Riemann surfaces, Bull. Amer. Math. Soc, 70 (1964), 110–112.Google Scholar
[A2] Ailing, N., Extensions of meromorphic function rings over non-compact Riemann surfaces. I, Math. Z., 89 (1965), 273–299.CrossRefGoogle Scholar
[B1] Behrens, M., The corona conjecture for a class of infinitely connected domains, Bull. Amer. Math. Soc, 76 (1970), 387–391.Google Scholar
[B2] Behrens, M., The maximal ideal space of algebras of bounded analytic functions on infinitely connected domains, Trans. Amer. Math. Soc, 161 (1971), 359–379.CrossRefGoogle Scholar
[BR] Berndtsson, B. and Ransford, T., Analytic multifunctions, the 9-equation and a proof of the corona theorem, Pacific J. Math., 124 (1986), 57–72.Google Scholar
[C1] Carleson, L., Interpolations by bounded analytic functions and the corona problem, Ann. of Math., 76 (1962), 547–559.CrossRefGoogle Scholar
[C2] Carleson, L., On H∞ in multiply connected domains, Conference on harmonic analysis in honor of Antoni Zygmund, Vol II, Beckner, W., et al., Wadsworth, 1983, 349–372.Google Scholar
[Ce] Cegrell, U., A generalization of the corona theorem in the unit disc, Math. Z., 203 (1990), 255–261.Google Scholar
[D] Deeb, W., A class of infinitely connected domains and the corona, Trans. Amer. Math. Soc, 231 (1977), 101–106.Google Scholar
[DW] Deeb, W. and Wilken, D., Δ-domains and the corona, Trans. Amer. Math. Soc, 231 (1977), 107–115.Google Scholar
[EM1] Earle, C. and Marden, A., Projections to automorphic functions, Proc. Amer. Math. Soc, 19 (1968), 274–278.Google Scholar
[EM2] Earle, C. and Marden, A., On Poincaré series with application to H p spaces on bordered Riemann surfaces, Illinois J. Math., 13 (1969), 202–219.Google Scholar
[F] Fisher, S., Function Theory on Planar Domains, Wiley-Interscience, 1983.Google Scholar
[Fo] Forelli, F., Bounded holomorphic functions and projections, Illinois J. Math., 10 (1966), 367–380.Google Scholar
[G1] Gamelin, T., Localization of the corona problem, Pacific J. Math., 34 (1970), 73–81.Google Scholar
[G2] Gamelin, T., Uniform Algebras and Jensen Measures, London Math. Soc. Lecture Note Series, 32, 1978.Google Scholar
[G3] Gamelin, T., Wolff’s proof of the corona problem, Israel J. Math., 37 (1980), 113–119.Google Scholar
[Ga] Garnett, J., Bounded Analytic Functions, Academic Press, 1981.Google Scholar
[GJ] Garnett, J. and Jones, P., The corona theorem for Denjoy domains, Acta Math., 155 (1985), 27–40.Google Scholar
[GM] Gorkin, P. and Mortini, R., F-ideals in QAB J. London Math. Soc, (2) 37 (1988), 509–519.Google Scholar
[H1] Hara, M., The corona problem on 2-sheeted disks, Proc. Japan Acad., 58 (1982), 256–257.Google Scholar
[H2] Hara, M., On Camelin constants, Pacific J. Math., 110 (1984), 77–81.Google Scholar
[HN] Hara, M. and Nakai, M., Corona theorem with bounds for finitely sheeted disks, Tohoku Math. J., 37 (1985), 225–240.Google Scholar
[Ha] Hatori, O., On T. Wolff’s problem (in Japanese), The Scientific Researches Math. (The School of Education, Waseda Univ.), 33 (1984), 41–49.Google Scholar
[JM] Jones, P. and Marshall, D., Critical points of Green’s function, harmonic measures, and the corona problem, Ark. Math., 23 (1985), 281–314.Google Scholar
[K] Koosis, P., Introduction to HP Spaces, London Math. Soc, Lecture Note Series 40, 1980.Google Scholar
[M] Moore, C., The corona theorem for domains whose boundary lies in a smooth curve, Proc Amer. Math. Soc, 100 (1987), 266–270.CrossRefGoogle Scholar
[Mo] Mortini, R., Corona theorems for subalgebras of H∞ Michigan Math. J., 36 (1989), 193–202.Google Scholar
[N1] Nakai, M., Corona problem for Riemann surfaces of Parreau-Widom type, Pacific J. Math., 103 (1982), 103–109.Google Scholar
[N2] Nakai, M., The corona problem on finitely sheeted covering surfaces, Nagoya Math. J., 92 (1983), 163–173.Google Scholar
[Na] Narita, J., A remark on the corona problem for plane domains, J. Math. Kyoto Univ., 25 (1985), 293–298.Google Scholar
[R] Rao, K., On a generalized corona problem, J. Analyse Math., 18 (1967), 277–278.Google Scholar
[SN] Sario, L. and Nakai, M., Classification Theory of Riemann Surfaces, Berlin-Heidelberg-New York: Springer, 1970.Google Scholar
[S1] Slodkowski, Z., An analytic set-valued selection and its applications to the corona theorem, to polynomical hulls and joint spectra, Trans. Amer. Math. Soc, 294 (1986), 367–377.CrossRefGoogle Scholar
[S2] Slodkowski, Z. , On bounded analytic functions in finitely connected domains, Trans. Amer. Math. Soc, 300 (1987), 721–736.Google Scholar
[St1] Stout, E., Two theorems concerning functions holomorphic on multiply connected domains, Bull. Amer. Math. Soc, 69 (1963), 527–530.Google Scholar
[St2] Stout, E., Some theorems on bounded holomorphic functions, Bull. Amer. Math. Soc, 70 (1964), 419–421.Google Scholar
[St3] Stout, E., Bounded holomorphic functions on finite Riemann surfaces, Trans. Amer. Math. Soc, 120 (1965), 255–285.Google Scholar
[Z] Zalcman, L., Bounded analytic functions on domains of infinite connectivity, Trans. Amer. Math. Soc, 144 (1969), 241–269.CrossRefGoogle Scholar