Published online by Cambridge University Press: 22 January 2016
Let T be the unit circle on the complex plane, H2(T) be the usual Hardy space on T, Tø be the Toeplitz operator with symbol 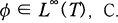 Cowen showed that if f1 and f2 are functions in H such that
Cowen showed that if f1 and f2 are functions in H such that 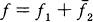 is in Lø, then Tf is hyponormal if and only if
is in Lø, then Tf is hyponormal if and only if 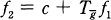 for some constant c and some function g in H∞ with
for some constant c and some function g in H∞ with 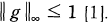 Using it, T. Nakazi and K. Takahashi showed that the symbol of hyponormal Toeplitz operator Tø satisfies
Using it, T. Nakazi and K. Takahashi showed that the symbol of hyponormal Toeplitz operator Tø satisfies 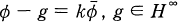 and
and 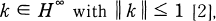 and they described the ø solving the functional equation above. Both of their conditions are hard to check, T. Nakazi and K. Takahashi remarked that even “the question about polynomials is still open” [2]. Kehe Zhu gave a computing process by way of Schur’s functions so that we can determine any given polynomial ø such that Tø is hyponormal [3]. Since no closed-form for the general Schur’s function is known, it is still valuable to find an explicit expression for the condition of a polynomial á such that Tø is hyponormal and depends only on the coefficients of ø, here we have one, it is elementary and relatively easy to check. We begin with the most general case and the following Lemma is essential.
and they described the ø solving the functional equation above. Both of their conditions are hard to check, T. Nakazi and K. Takahashi remarked that even “the question about polynomials is still open” [2]. Kehe Zhu gave a computing process by way of Schur’s functions so that we can determine any given polynomial ø such that Tø is hyponormal [3]. Since no closed-form for the general Schur’s function is known, it is still valuable to find an explicit expression for the condition of a polynomial á such that Tø is hyponormal and depends only on the coefficients of ø, here we have one, it is elementary and relatively easy to check. We begin with the most general case and the following Lemma is essential.