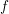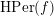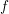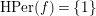1 Infra-nilmanifolds
Let
![]() $f:X\rightarrow X$
be a map on a topological space
$f:X\rightarrow X$
be a map on a topological space
![]() $X$
. We say that
$X$
. We say that
![]() $x\in X$
is a periodic point of
$x\in X$
is a periodic point of
![]() $f$
if
$f$
if
![]() $f^{n}(x)=x$
for some positive integer
$f^{n}(x)=x$
for some positive integer
![]() $n$
. If this is the case, we say that this positive integer
$n$
. If this is the case, we say that this positive integer
![]() $n$
is the pure period of
$n$
is the pure period of
![]() $x$
if
$x$
if
![]() $f^{l}(x)\neq x$
for all
$f^{l}(x)\neq x$
for all
![]() $l<n$
. In this paper, we study these periodic points when
$l<n$
. In this paper, we study these periodic points when
![]() $X$
is an infra-nilmanifold and we show that for a large class of maps
$X$
is an infra-nilmanifold and we show that for a large class of maps
![]() $f$
on such manifolds, there exists a positive integer
$f$
on such manifolds, there exists a positive integer
![]() $m$
such that any map
$m$
such that any map
![]() $g$
homotopic to
$g$
homotopic to
![]() $f$
admits points of pure period
$f$
admits points of pure period
![]() $k$
for any
$k$
for any
![]() $k\in [m,+\infty )$
. In the first section, we recall the necessary background on the class of infra-nilmanifolds and their maps. In the next section, we give a more detailed description of the theory of fixed and periodic points. The third and last section is devoted to the proof of our main result.
$k\in [m,+\infty )$
. In the first section, we recall the necessary background on the class of infra-nilmanifolds and their maps. In the next section, we give a more detailed description of the theory of fixed and periodic points. The third and last section is devoted to the proof of our main result.
Every infra-nilmanifold is modeled on a connected and simply connected nilpotent Lie group. Given such a Lie group
![]() $G$
, we consider its group of affine transformations
$G$
, we consider its group of affine transformations
![]() $\operatorname{Aff}(G)=G\mathbb{o}\operatorname{Aut}(G)$
, which admits a natural left action on the Lie group
$\operatorname{Aff}(G)=G\mathbb{o}\operatorname{Aut}(G)$
, which admits a natural left action on the Lie group
![]() $G$
:
$G$
:
Note that when
![]() $G$
is abelian,
$G$
is abelian,
![]() $G$
is isomorphic to
$G$
is isomorphic to
![]() $\mathbb{R}^{n}$
for some
$\mathbb{R}^{n}$
for some
![]() $n$
and
$n$
and
![]() $\operatorname{Aff}(G)$
is the usual affine group
$\operatorname{Aff}(G)$
is the usual affine group
![]() $\operatorname{Aff}(\mathbb{R}^{n})$
with its usual action on the affine space
$\operatorname{Aff}(\mathbb{R}^{n})$
with its usual action on the affine space
![]() $\mathbb{R}^{n}$
. Let
$\mathbb{R}^{n}$
. Let
![]() $p:\operatorname{Aff}(G)=G\mathbb{o}\operatorname{Aut}(G)\rightarrow \operatorname{Aut}(G)$
denote the natural projection onto the second factor.
$p:\operatorname{Aff}(G)=G\mathbb{o}\operatorname{Aut}(G)\rightarrow \operatorname{Aut}(G)$
denote the natural projection onto the second factor.
Definition 1.1. A subgroup
![]() $\unicode[STIX]{x1D6E4}\subseteq \operatorname{Aff}(G)$
is called almost-crystallographic if and only if
$\unicode[STIX]{x1D6E4}\subseteq \operatorname{Aff}(G)$
is called almost-crystallographic if and only if
![]() $p(\unicode[STIX]{x1D6E4})$
is finite and
$p(\unicode[STIX]{x1D6E4})$
is finite and
![]() $\unicode[STIX]{x1D6E4}\cap G$
is a uniform and discrete subgroup of
$\unicode[STIX]{x1D6E4}\cap G$
is a uniform and discrete subgroup of
![]() $G$
. The finite group
$G$
. The finite group
![]() $F=p(\unicode[STIX]{x1D6E4})$
is called the holonomy group of
$F=p(\unicode[STIX]{x1D6E4})$
is called the holonomy group of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
The action of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $G$
is properly discontinuous and cocompact and when
$G$
is properly discontinuous and cocompact and when
![]() $\unicode[STIX]{x1D6E4}$
is torsion-free, this action becomes a free action, from which we can conclude that the resulting quotient space
$\unicode[STIX]{x1D6E4}$
is torsion-free, this action becomes a free action, from which we can conclude that the resulting quotient space
![]() $\unicode[STIX]{x1D6E4}\backslash G$
is a compact manifold with fundamental group
$\unicode[STIX]{x1D6E4}\backslash G$
is a compact manifold with fundamental group
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Definition 1.2. A torsion-free almost-crystallographic group
![]() $\unicode[STIX]{x1D6E4}\subseteq \operatorname{Aff}(G)$
is called an almost-Bieberbach group, and the corresponding manifold
$\unicode[STIX]{x1D6E4}\subseteq \operatorname{Aff}(G)$
is called an almost-Bieberbach group, and the corresponding manifold
![]() $\unicode[STIX]{x1D6E4}\backslash G$
is called an infra-nilmanifold (modeled on
$\unicode[STIX]{x1D6E4}\backslash G$
is called an infra-nilmanifold (modeled on
![]() $G$
).
$G$
).
When the holonomy group is trivial,
![]() $\unicode[STIX]{x1D6E4}$
will be a lattice in
$\unicode[STIX]{x1D6E4}$
will be a lattice in
![]() $G$
and the corresponding manifold
$G$
and the corresponding manifold
![]() $\unicode[STIX]{x1D6E4}\backslash G$
is a nilmanifold. When
$\unicode[STIX]{x1D6E4}\backslash G$
is a nilmanifold. When
![]() $G$
is abelian,
$G$
is abelian,
![]() $\unicode[STIX]{x1D6E4}$
will be called a Bieberbach group and
$\unicode[STIX]{x1D6E4}$
will be called a Bieberbach group and
![]() $\unicode[STIX]{x1D6E4}\backslash G$
a compact flat manifold. When
$\unicode[STIX]{x1D6E4}\backslash G$
a compact flat manifold. When
![]() $G$
is abelian and the holonomy group of
$G$
is abelian and the holonomy group of
![]() $\unicode[STIX]{x1D6E4}$
is trivial, then
$\unicode[STIX]{x1D6E4}$
is trivial, then
![]() $\unicode[STIX]{x1D6E4}$
is just a lattice in some
$\unicode[STIX]{x1D6E4}$
is just a lattice in some
![]() $\mathbb{R}^{n}$
and
$\mathbb{R}^{n}$
and
![]() $\unicode[STIX]{x1D6E4}\backslash G$
is a torus.
$\unicode[STIX]{x1D6E4}\backslash G$
is a torus.
Now, define the semigroup
![]() $\operatorname{aff}(G)=G\mathbb{o}\operatorname{Endo}(G)$
, where
$\operatorname{aff}(G)=G\mathbb{o}\operatorname{Endo}(G)$
, where
![]() $\operatorname{Endo}(G)$
is the set of continuous endomorphisms of
$\operatorname{Endo}(G)$
is the set of continuous endomorphisms of
![]() $G$
. Note that
$G$
. Note that
![]() $\operatorname{aff}(G)$
acts on
$\operatorname{aff}(G)$
acts on
![]() $G$
in a similar way as
$G$
in a similar way as
![]() $\operatorname{Aff}(G)$
, that is, any element
$\operatorname{Aff}(G)$
, that is, any element
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
of
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
of
![]() $\operatorname{aff}(G)$
can be seen as a self-map of
$\operatorname{aff}(G)$
can be seen as a self-map of
![]() $G$
:
$G$
:
and we refer to
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
as an affine map of
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
as an affine map of
![]() $G$
. One of the nice features of infra-nilmanifolds is that any map on a infra-nilmanifold is homotopic to a map which is induced by an affine map of
$G$
. One of the nice features of infra-nilmanifolds is that any map on a infra-nilmanifold is homotopic to a map which is induced by an affine map of
![]() $G$
. One can prove this by using the following result by Lee.
$G$
. One can prove this by using the following result by Lee.
Theorem 1.3. (Lee [Reference Lee18])
Let
![]() $G$
be a connected and simply connected nilpotent Lie group and suppose that
$G$
be a connected and simply connected nilpotent Lie group and suppose that
![]() $\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}^{\prime }\subseteq \operatorname{Aff}(G)$
are two almost-crystallographic groups modeled on
$\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}^{\prime }\subseteq \operatorname{Aff}(G)$
are two almost-crystallographic groups modeled on
![]() $G$
. Then for any homomorphism
$G$
. Then for any homomorphism
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
there exists an element
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
there exists an element
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})\in \operatorname{aff}(G)$
such that
$(\unicode[STIX]{x1D6FF},\mathfrak{D})\in \operatorname{aff}(G)$
such that
Note that we can consider the equality
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FE})(\unicode[STIX]{x1D6FF},\mathfrak{D})=(\unicode[STIX]{x1D6FF},\mathfrak{D})\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FE})(\unicode[STIX]{x1D6FF},\mathfrak{D})=(\unicode[STIX]{x1D6FF},\mathfrak{D})\unicode[STIX]{x1D6FE}$
in
![]() $\operatorname{aff}(G)$
, since
$\operatorname{aff}(G)$
, since
![]() $\operatorname{Aff}(G)$
is contained in
$\operatorname{Aff}(G)$
is contained in
![]() $\operatorname{aff}(G)$
. With this equality in mind, it is easy to see that the affine map
$\operatorname{aff}(G)$
. With this equality in mind, it is easy to see that the affine map
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
induces a well-defined map
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
induces a well-defined map
which exactly induces the morphism
![]() $\unicode[STIX]{x1D711}$
on the level of the fundamental groups.
$\unicode[STIX]{x1D711}$
on the level of the fundamental groups.
On the other hand, if we choose an arbitrary map
![]() $f:\unicode[STIX]{x1D6E4}\backslash G\rightarrow \unicode[STIX]{x1D6E4}^{\prime }\backslash G$
between two infra-nilmanifolds and choose a lifting
$f:\unicode[STIX]{x1D6E4}\backslash G\rightarrow \unicode[STIX]{x1D6E4}^{\prime }\backslash G$
between two infra-nilmanifolds and choose a lifting
![]() $\tilde{f}:G\rightarrow G$
of
$\tilde{f}:G\rightarrow G$
of
![]() $f$
, then there exists a morphism
$f$
, then there exists a morphism
![]() $\tilde{f}_{\ast }:\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
such that
$\tilde{f}_{\ast }:\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
such that
![]() $\tilde{f}_{\ast }(\unicode[STIX]{x1D6FE})\circ \tilde{f}=\tilde{f}\circ \unicode[STIX]{x1D6FE}$
, for all
$\tilde{f}_{\ast }(\unicode[STIX]{x1D6FE})\circ \tilde{f}=\tilde{f}\circ \unicode[STIX]{x1D6FE}$
, for all
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
. By Theorem 1.3, an affine map
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
. By Theorem 1.3, an affine map
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})\in \operatorname{aff}(G)$
exists which also satisfies
$(\unicode[STIX]{x1D6FF},\mathfrak{D})\in \operatorname{aff}(G)$
exists which also satisfies
![]() $\tilde{f}_{\ast }(\unicode[STIX]{x1D6FE})\circ (\unicode[STIX]{x1D6FF},\mathfrak{D})=(\unicode[STIX]{x1D6FF},\mathfrak{D})\circ \unicode[STIX]{x1D6FE}$
for all
$\tilde{f}_{\ast }(\unicode[STIX]{x1D6FE})\circ (\unicode[STIX]{x1D6FF},\mathfrak{D})=(\unicode[STIX]{x1D6FF},\mathfrak{D})\circ \unicode[STIX]{x1D6FE}$
for all
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
. Therefore, the induced map
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
. Therefore, the induced map
![]() $\overline{(\unicode[STIX]{x1D6FF},D)}$
and
$\overline{(\unicode[STIX]{x1D6FF},D)}$
and
![]() $f$
are homotopic. We call
$f$
are homotopic. We call
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
an affine homotopy lift of
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
an affine homotopy lift of
![]() $f$
.
$f$
.
We end this introduction about infra-nilmanifolds with the definition of a hyperbolic map on an infra-nilmanifold. We denote by
![]() $\mathfrak{D}_{\ast }$
the Lie algebra endomorphism induced by
$\mathfrak{D}_{\ast }$
the Lie algebra endomorphism induced by
![]() $\mathfrak{D}$
on the Lie algebra
$\mathfrak{D}$
on the Lie algebra
![]() $\mathfrak{g}$
associated to
$\mathfrak{g}$
associated to
![]() $G$
.
$G$
.
Definition 1.4. Let
![]() $M$
be an infra-nilmanifold and
$M$
be an infra-nilmanifold and
![]() $f:M\rightarrow M$
be a continuous map, with
$f:M\rightarrow M$
be a continuous map, with
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
as an affine homotopy lift. We say that
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
as an affine homotopy lift. We say that
![]() $f$
is a hyperbolic map if
$f$
is a hyperbolic map if
![]() $\mathfrak{D}_{\ast }$
has no eigenvalues of modulus
$\mathfrak{D}_{\ast }$
has no eigenvalues of modulus
![]() $1$
.
$1$
.
Remark 1.5. The map
![]() $\mathfrak{D}$
, and hence also
$\mathfrak{D}$
, and hence also
![]() $\mathfrak{D}_{\ast }$
depends on the choice of the lift
$\mathfrak{D}_{\ast }$
depends on the choice of the lift
![]() $\tilde{f}$
. Once the lift
$\tilde{f}$
. Once the lift
![]() $\tilde{f}$
is fixed, and hence the morphism
$\tilde{f}$
is fixed, and hence the morphism
![]() $\tilde{f}_{\ast }$
is fixed, the
$\tilde{f}_{\ast }$
is fixed, the
![]() $\mathfrak{D}$
– part of the map
$\mathfrak{D}$
– part of the map
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
in Theorem 1.3 is also fixed (although the
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
in Theorem 1.3 is also fixed (although the
![]() $\unicode[STIX]{x1D6FF}$
– part is not unique in general). It follows that
$\unicode[STIX]{x1D6FF}$
– part is not unique in general). It follows that
![]() $f$
determines
$f$
determines
![]() $\mathfrak{D}$
only up to an inner automorphism of
$\mathfrak{D}$
only up to an inner automorphism of
![]() $G$
. But as inner automorphisms have no effect on the eigenvalues of
$G$
. But as inner automorphisms have no effect on the eigenvalues of
![]() $\mathfrak{D}_{\ast }$
(in the case of a nilpotent Lie group
$\mathfrak{D}_{\ast }$
(in the case of a nilpotent Lie group
![]() $G$
) the notion of a hyperbolic map is well defined.
$G$
) the notion of a hyperbolic map is well defined.
Two important classes of maps on infra-nilmanifolds which are hyperbolic are the expanding maps and the Anosov diffeomorphisms.
Remark 1.6. Due to [Reference Dekimpe, De Rock and Malfait4, Lemma 4.5], it is known that every nowhere expanding map on an infra-nilmanifold only has eigenvalues
![]() $0$
or eigenvalues of modulus
$0$
or eigenvalues of modulus
![]() $1$
. This means that every hyperbolic map for which
$1$
. This means that every hyperbolic map for which
![]() $\mathfrak{D}_{\ast }$
is not nilpotent has an eigenvalue of modulus strictly bigger than
$\mathfrak{D}_{\ast }$
is not nilpotent has an eigenvalue of modulus strictly bigger than
![]() $1$
.
$1$
.
2 Nielsen theory, dynamical zeta functions and
 $\operatorname{HPer}(f)$
$\operatorname{HPer}(f)$
Let
![]() $f:X\rightarrow X$
be a self-map of a compact polyhedron
$f:X\rightarrow X$
be a self-map of a compact polyhedron
![]() $X$
. There are different ways to assign integers to this map
$X$
. There are different ways to assign integers to this map
![]() $f$
that give information about the fixed points of
$f$
that give information about the fixed points of
![]() $f$
. One of these integers is the Lefschetz number
$f$
. One of these integers is the Lefschetz number
![]() $L(f)$
which is defined as
$L(f)$
which is defined as
In our situation, the space
![]() $X=\unicode[STIX]{x1D6E4}\backslash G$
will be a infra-nilmanifold, which is an aspherical space, and hence the (co)homology of the space
$X=\unicode[STIX]{x1D6E4}\backslash G$
will be a infra-nilmanifold, which is an aspherical space, and hence the (co)homology of the space
![]() $X=\unicode[STIX]{x1D6E4}\backslash G$
equals the (co)homology of the group
$X=\unicode[STIX]{x1D6E4}\backslash G$
equals the (co)homology of the group
![]() $\unicode[STIX]{x1D6E4}$
. It follows that in this case we have (see also [Reference Jezierski and Marzantowicz13, p. 36])
$\unicode[STIX]{x1D6E4}$
. It follows that in this case we have (see also [Reference Jezierski and Marzantowicz13, p. 36])
 $$\begin{eqnarray}\displaystyle L(f) & = & \displaystyle \mathop{\sum }_{i=0}^{\operatorname{dim}\;X}(-1)^{i}\operatorname{Tr}(f_{\ast ,i}:H_{i}(\unicode[STIX]{x1D6E4},\mathbb{R})\rightarrow H_{i}(\unicode[STIX]{x1D6E4},\mathbb{R}))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=0}^{\operatorname{dim}\;X}(-1)^{i}\operatorname{Tr}(f_{i}^{\ast }:H^{i}(\unicode[STIX]{x1D6E4},\mathbb{R})\rightarrow H^{i}(\unicode[STIX]{x1D6E4},\mathbb{R})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L(f) & = & \displaystyle \mathop{\sum }_{i=0}^{\operatorname{dim}\;X}(-1)^{i}\operatorname{Tr}(f_{\ast ,i}:H_{i}(\unicode[STIX]{x1D6E4},\mathbb{R})\rightarrow H_{i}(\unicode[STIX]{x1D6E4},\mathbb{R}))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=0}^{\operatorname{dim}\;X}(-1)^{i}\operatorname{Tr}(f_{i}^{\ast }:H^{i}(\unicode[STIX]{x1D6E4},\mathbb{R})\rightarrow H^{i}(\unicode[STIX]{x1D6E4},\mathbb{R})).\nonumber\end{eqnarray}$$
The Lefschetz fixed point theorem states that if
![]() $L(f)\neq 0$
, then
$L(f)\neq 0$
, then
![]() $f$
has at least one fixed point. Because the Lefschetz number is only defined in terms of (co)homology groups, it remains invariant under a homotopy and hence, if
$f$
has at least one fixed point. Because the Lefschetz number is only defined in terms of (co)homology groups, it remains invariant under a homotopy and hence, if
![]() $L(f)\neq 0$
, the Lefschetz fixed point theorem guarantees that any map homotopic to
$L(f)\neq 0$
, the Lefschetz fixed point theorem guarantees that any map homotopic to
![]() $f$
also has at least one fixed point.
$f$
also has at least one fixed point.
Another integer giving information on the fixed points of
![]() $f$
is the Nielsen number
$f$
is the Nielsen number
![]() $N(f)$
. It is a homotopy-invariant lower bound for the number of fixed points of
$N(f)$
. It is a homotopy-invariant lower bound for the number of fixed points of
![]() $f$
. To define
$f$
. To define
![]() $N(f)$
, fix a reference lifting
$N(f)$
, fix a reference lifting
![]() $\tilde{f}$
of
$\tilde{f}$
of
![]() $f$
with respect to a universal cover
$f$
with respect to a universal cover
![]() $(\tilde{X},p)$
of
$(\tilde{X},p)$
of
![]() $X$
and denote the group of covering transformations by
$X$
and denote the group of covering transformations by
![]() ${\mathcal{D}}$
. For
${\mathcal{D}}$
. For
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{D}}$
, the sets
$\unicode[STIX]{x1D6FC}\in {\mathcal{D}}$
, the sets
![]() $p(\operatorname{Fix}(\unicode[STIX]{x1D6FC}\circ \tilde{f}))$
form a partition of the fixed point set
$p(\operatorname{Fix}(\unicode[STIX]{x1D6FC}\circ \tilde{f}))$
form a partition of the fixed point set
![]() $\operatorname{Fix}(f)$
. These sets are called fixed point classes. By using the fixed point index, we can assign an integer to each fixed point class in such a way that if a nonzero integer is assigned, the fixed point class cannot completely vanish under a homotopy. Such a nonvanishing fixed point class will be called essential and
$\operatorname{Fix}(f)$
. These sets are called fixed point classes. By using the fixed point index, we can assign an integer to each fixed point class in such a way that if a nonzero integer is assigned, the fixed point class cannot completely vanish under a homotopy. Such a nonvanishing fixed point class will be called essential and
![]() $N(f)$
is defined as the number of essential fixed point classes of
$N(f)$
is defined as the number of essential fixed point classes of
![]() $f$
.
$f$
.
By definition, it is clear that
![]() $N(f)$
will indeed be a homotopy-invariant lower bound for the number of fixed points of
$N(f)$
will indeed be a homotopy-invariant lower bound for the number of fixed points of
![]() $f$
. Hence, in general,
$f$
. Hence, in general,
![]() $N(f)$
will give more information about the fixed points of
$N(f)$
will give more information about the fixed points of
![]() $f$
than
$f$
than
![]() $L(f)$
. The downside, however, is that Nielsen numbers are often much harder to compute than Lefschetz numbers, because the fixed point index can be a tedious thing to work with. Luckily, on infra-nilmanifolds there exists an algebraic formula to compute
$L(f)$
. The downside, however, is that Nielsen numbers are often much harder to compute than Lefschetz numbers, because the fixed point index can be a tedious thing to work with. Luckily, on infra-nilmanifolds there exists an algebraic formula to compute
![]() $N(f)$
, which makes them a convenient class of manifolds to study Nielsen theory on. More information on both
$N(f)$
, which makes them a convenient class of manifolds to study Nielsen theory on. More information on both
![]() $L(f)$
and
$L(f)$
and
![]() $N(f)$
can be found in for example, [Reference Brown3, Reference Jiang14, Reference Kiang15].
$N(f)$
can be found in for example, [Reference Brown3, Reference Jiang14, Reference Kiang15].
By using the Lefschetz and Nielsen numbers of iterates of
![]() $f$
as coefficients, it is possible to define the so-called dynamical zeta functions. The Lefschetz zeta function was introduced by Smale in [Reference Smale21]:
$f$
as coefficients, it is possible to define the so-called dynamical zeta functions. The Lefschetz zeta function was introduced by Smale in [Reference Smale21]:
In his paper, Smale also proved that the Lefschetz zeta function is always rational for self-maps on compact polyhedra.
The proof is actually quite straightforward. Let the
![]() $\unicode[STIX]{x1D706}_{ij}$
’s denote the eigenvalues of
$\unicode[STIX]{x1D706}_{ij}$
’s denote the eigenvalues of
![]() $f_{\ast }^{i}:H^{i}(X,\mathbb{R})\rightarrow H^{i}(X,\mathbb{R})$
, with
$f_{\ast }^{i}:H^{i}(X,\mathbb{R})\rightarrow H^{i}(X,\mathbb{R})$
, with
![]() $j\in \{1,\ldots ,\operatorname{dim}(H^{i}(X,\mathbb{R}))\}$
. Because the trace of a matrix is the sum of the eigenvalues, we find
$j\in \{1,\ldots ,\operatorname{dim}(H^{i}(X,\mathbb{R}))\}$
. Because the trace of a matrix is the sum of the eigenvalues, we find
 $$\begin{eqnarray}L_{f}(z)=\exp \left(\mathop{\sum }_{k=1}^{+\infty }\left(\mathop{\sum }_{i=0}^{\operatorname{dim}\;X}(-1)^{i}\mathop{\sum }_{j=1}^{\operatorname{dim}\;H^{i}(X)}\unicode[STIX]{x1D706}_{ij}^{k}\right)\frac{z^{k}}{k}\right).\end{eqnarray}$$
$$\begin{eqnarray}L_{f}(z)=\exp \left(\mathop{\sum }_{k=1}^{+\infty }\left(\mathop{\sum }_{i=0}^{\operatorname{dim}\;X}(-1)^{i}\mathop{\sum }_{j=1}^{\operatorname{dim}\;H^{i}(X)}\unicode[STIX]{x1D706}_{ij}^{k}\right)\frac{z^{k}}{k}\right).\end{eqnarray}$$
By reordering the terms and by using the fact that
it is easy to derive that
 $$\begin{eqnarray}L_{f}(z)=\mathop{\prod }_{i=0}^{\operatorname{dim}\;X}\mathop{\prod }_{j=1}^{\operatorname{dim}\;H^{i}(X)}(1-\unicode[STIX]{x1D706}_{ij}z)^{(-1)^{i+1}}.\end{eqnarray}$$
$$\begin{eqnarray}L_{f}(z)=\mathop{\prod }_{i=0}^{\operatorname{dim}\;X}\mathop{\prod }_{j=1}^{\operatorname{dim}\;H^{i}(X)}(1-\unicode[STIX]{x1D706}_{ij}z)^{(-1)^{i+1}}.\end{eqnarray}$$
Remark 2.1. Suppose that
![]() $\unicode[STIX]{x1D6EC}$
is a lattice of a connected and simply connected nilpotent Lie group
$\unicode[STIX]{x1D6EC}$
is a lattice of a connected and simply connected nilpotent Lie group
![]() $G$
and
$G$
and
![]() $f:\unicode[STIX]{x1D6EC}\backslash G\rightarrow \unicode[STIX]{x1D6EC}\backslash G$
is a self-map of the nilmanifold
$f:\unicode[STIX]{x1D6EC}\backslash G\rightarrow \unicode[STIX]{x1D6EC}\backslash G$
is a self-map of the nilmanifold
![]() $\unicode[STIX]{x1D6EC}\backslash G$
with affine homotopy lift
$\unicode[STIX]{x1D6EC}\backslash G$
with affine homotopy lift
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
. Let
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
. Let
![]() $\mathfrak{D}_{\ast }$
be the induced linear map on the Lie algebra
$\mathfrak{D}_{\ast }$
be the induced linear map on the Lie algebra
![]() $\mathfrak{g}$
of
$\mathfrak{g}$
of
![]() $G$
as before. The main result of [Reference Nomizu19] states that there are natural isomorphisms
$G$
as before. The main result of [Reference Nomizu19] states that there are natural isomorphisms
The naturality of these automorphisms implies that there is a commutative diagram

Here
![]() $\mathfrak{D}_{\ast }^{i}$
is the map induced by
$\mathfrak{D}_{\ast }^{i}$
is the map induced by
![]() $\mathfrak{D}_{\ast }$
on the
$\mathfrak{D}_{\ast }$
on the
![]() $i$
th cohomology space of
$i$
th cohomology space of
![]() $\mathfrak{g}$
. Recall, that the cohomology of
$\mathfrak{g}$
. Recall, that the cohomology of
![]() $\mathfrak{g}$
is defined as the cohomology of a cochain complex, where the
$\mathfrak{g}$
is defined as the cohomology of a cochain complex, where the
![]() $i$
th term is Hom
$i$
th term is Hom
![]() $(\bigwedge ^{i}\mathfrak{g},\mathbb{R})=(\bigwedge ^{i}\mathfrak{g})^{\ast }$
, the dual space of
$(\bigwedge ^{i}\mathfrak{g},\mathbb{R})=(\bigwedge ^{i}\mathfrak{g})^{\ast }$
, the dual space of
![]() $\bigwedge ^{i}\mathfrak{g}$
. So,
$\bigwedge ^{i}\mathfrak{g}$
. So,
![]() $\mathfrak{D}_{\ast }^{i}$
is induced by the dual map of
$\mathfrak{D}_{\ast }^{i}$
is induced by the dual map of
![]() $\bigwedge ^{i}\mathfrak{D}_{\ast }$
. Since this dual map and
$\bigwedge ^{i}\mathfrak{D}_{\ast }$
. Since this dual map and
![]() $\bigwedge ^{i}\mathfrak{D}_{\ast }$
have the same eigenvalues, it follows that the set of eigenvalues of
$\bigwedge ^{i}\mathfrak{D}_{\ast }$
have the same eigenvalues, it follows that the set of eigenvalues of
![]() $\mathfrak{D}_{\ast }^{i}$
, hence also the set of eigenvalues
$\mathfrak{D}_{\ast }^{i}$
, hence also the set of eigenvalues
![]() $\unicode[STIX]{x1D706}_{i,j}$
of
$\unicode[STIX]{x1D706}_{i,j}$
of
![]() $f_{i}^{\ast }$
in expression (1), is a subset of the set of eigenvalues of
$f_{i}^{\ast }$
in expression (1), is a subset of the set of eigenvalues of
![]() $\bigwedge ^{i}\mathfrak{D}_{\ast }:\bigwedge ^{i}\mathfrak{g}\rightarrow \bigwedge ^{i}\mathfrak{g}$
. (This fact is also reflected in the formula obtained in [Reference Fel’shtyn7, Theorem 23].)
$\bigwedge ^{i}\mathfrak{D}_{\ast }:\bigwedge ^{i}\mathfrak{g}\rightarrow \bigwedge ^{i}\mathfrak{g}$
. (This fact is also reflected in the formula obtained in [Reference Fel’shtyn7, Theorem 23].)
The Nielsen zeta function was introduced by Fel’shtyn in [Reference Fel’shtyn10, Reference Pilyugina and Fel’shtyn20] and is defined in a similar way as the Lefschetz zeta function:
It is known that this zeta function does not always have to be a rational function. A counterexample for this can be found in [Reference Fel’shtyn7], for example, in Remark 7.
For self-maps on infra-nilmanifolds, however, the Nielsen zeta function will always be rational. To prove this, one can exploit the fact that
![]() $N(f)$
and
$N(f)$
and
![]() $L(f)$
are very closely related. In [Reference Dekimpe and Dugardein5], we defined a subgroup
$L(f)$
are very closely related. In [Reference Dekimpe and Dugardein5], we defined a subgroup
![]() $\unicode[STIX]{x1D6E4}_{+}$
of
$\unicode[STIX]{x1D6E4}_{+}$
of
![]() $\unicode[STIX]{x1D6E4}$
, which equals
$\unicode[STIX]{x1D6E4}$
, which equals
![]() $\unicode[STIX]{x1D6E4}$
or is of index
$\unicode[STIX]{x1D6E4}$
or is of index
![]() $2$
in
$2$
in
![]() $\unicode[STIX]{x1D6E4}$
. The precise definition is not of major significance for the rest of this paper. However, it allowed us to write
$\unicode[STIX]{x1D6E4}$
. The precise definition is not of major significance for the rest of this paper. However, it allowed us to write
![]() $N_{f}(z)$
as a function of
$N_{f}(z)$
as a function of
![]() $L_{f}(z)$
if
$L_{f}(z)$
if
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{+}$
, and as a combination of
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{+}$
, and as a combination of
![]() $L_{f}(z)$
and
$L_{f}(z)$
and
![]() $L_{f_{+}}(z)$
if
$L_{f_{+}}(z)$
if
![]() $[\unicode[STIX]{x1D6E4}:\unicode[STIX]{x1D6E4}_{+}]=2$
. Here,
$[\unicode[STIX]{x1D6E4}:\unicode[STIX]{x1D6E4}_{+}]=2$
. Here,
![]() $f_{+}:\unicode[STIX]{x1D6E4}_{+}\backslash G\rightarrow \unicode[STIX]{x1D6E4}_{+}\backslash G$
is a lift of
$f_{+}:\unicode[STIX]{x1D6E4}_{+}\backslash G\rightarrow \unicode[STIX]{x1D6E4}_{+}\backslash G$
is a lift of
![]() $f$
to the
$f$
to the
![]() $2$
-folded covering space
$2$
-folded covering space
![]() $\unicode[STIX]{x1D6E4}_{+}\backslash G$
of
$\unicode[STIX]{x1D6E4}_{+}\backslash G$
of
![]() $\unicode[STIX]{x1D6E4}\backslash G$
. The following theorem, together with the fact that Lefschetz zeta functions are always rational, therefore proves the rationality of Nielsen zeta functions for infra-nilmanifolds.
$\unicode[STIX]{x1D6E4}\backslash G$
. The following theorem, together with the fact that Lefschetz zeta functions are always rational, therefore proves the rationality of Nielsen zeta functions for infra-nilmanifolds.
Theorem 2.2. [Reference Dekimpe and Dugardein5, Theorem 4.6]
Let
![]() $M=\unicode[STIX]{x1D6E4}\backslash G$
be an infra-nilmanifold and let
$M=\unicode[STIX]{x1D6E4}\backslash G$
be an infra-nilmanifold and let
![]() $f:M\rightarrow M$
be a self-map with affine homotopy lift
$f:M\rightarrow M$
be a self-map with affine homotopy lift
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
. Let
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
. Let
![]() $p$
denote the number of positive real eigenvalues of
$p$
denote the number of positive real eigenvalues of
![]() $\mathfrak{D}_{\ast }$
which are strictly greater than
$\mathfrak{D}_{\ast }$
which are strictly greater than
![]() $1$
and let
$1$
and let
![]() $n$
denote the number of negative real eigenvalues of
$n$
denote the number of negative real eigenvalues of
![]() $\mathfrak{D}_{\ast }$
which are strictly less than
$\mathfrak{D}_{\ast }$
which are strictly less than
![]() $-1$
. Then we have the following table of equations:
$-1$
. Then we have the following table of equations:

Moreover, this theorem also tells us that we can write
![]() $N_{f}(z)$
in a similar form as in equation (1), since every Lefschetz zeta function is of this form. More information about dynamical zeta functions can be found in [Reference Fel’shtyn7].
$N_{f}(z)$
in a similar form as in equation (1), since every Lefschetz zeta function is of this form. More information about dynamical zeta functions can be found in [Reference Fel’shtyn7].
Closely related to fixed point theory, is periodic point theory. We call
![]() $x\in X$
a periodic point of
$x\in X$
a periodic point of
![]() $f$
if there exists a positive integer
$f$
if there exists a positive integer
![]() $n$
, such that
$n$
, such that
![]() $f^{n}(x)=x$
. Of course, when
$f^{n}(x)=x$
. Of course, when
![]() $f^{n}(x)=x$
, this does not automatically imply that the actual period of
$f^{n}(x)=x$
, this does not automatically imply that the actual period of
![]() $x$
is
$x$
is
![]() $n$
. For example, it is immediately clear that every fixed point is also a periodic point of period
$n$
. For example, it is immediately clear that every fixed point is also a periodic point of period
![]() $n$
, for all
$n$
, for all
![]() $n>0$
. In order to exclude these points, we define the set of periodic points of pure period
$n>0$
. In order to exclude these points, we define the set of periodic points of pure period
![]() $n$
:
$n$
:
The set of homotopy minimal periods of
![]() $f$
is then defined as the following subset of the positive integers:
$f$
is then defined as the following subset of the positive integers:
This set has been studied extensively, for example, in [Reference Alsedà, Baldwin, Llibre, Swanson and Szlenk1] for maps on the torus, in [Reference Jezierski and Marzantowicz12] for maps on nilmanifolds and in [Reference Fel’shtyn and Lee9, Reference Lee and Zhao17] for maps on infra-nilmanifolds.
Just as Nielsen fixed point theory divides
![]() $\operatorname{Fix}(f)$
into different fixed point classes, Nielsen periodic point theory divides
$\operatorname{Fix}(f)$
into different fixed point classes, Nielsen periodic point theory divides
![]() $\operatorname{Fix}(f^{n})$
into different fixed point classes, for all
$\operatorname{Fix}(f^{n})$
into different fixed point classes, for all
![]() $n>0$
and looks for relations between fixed point classes on different levels. This idea is covered by the following definition.
$n>0$
and looks for relations between fixed point classes on different levels. This idea is covered by the following definition.
Definition 2.3. Let
![]() $f:X\rightarrow X$
be a self-map. If
$f:X\rightarrow X$
be a self-map. If
![]() $\mathbb{F}_{k}$
is a fixed point class of
$\mathbb{F}_{k}$
is a fixed point class of
![]() $f^{k}$
, then
$f^{k}$
, then
![]() $\mathbb{F}_{k}$
will be contained in a fixed point class
$\mathbb{F}_{k}$
will be contained in a fixed point class
![]() $\mathbb{F}_{kn}$
of
$\mathbb{F}_{kn}$
of
![]() $(f^{k})^{n}$
, for all
$(f^{k})^{n}$
, for all
![]() $n$
. We say that
$n$
. We say that
![]() $\mathbb{F}_{k}$
boosts to
$\mathbb{F}_{k}$
boosts to
![]() $\mathbb{F}_{kn}$
. On the other hand, we say that
$\mathbb{F}_{kn}$
. On the other hand, we say that
![]() $\mathbb{F}_{kn}$
reduces to
$\mathbb{F}_{kn}$
reduces to
![]() $\mathbb{F}_{k}$
.
$\mathbb{F}_{k}$
.
An important definition that gives some structure to the boosting and reducing relations is the following.
Definition 2.4. A self-map
![]() $f:X\rightarrow X$
will be called essentially reducible if, for all
$f:X\rightarrow X$
will be called essentially reducible if, for all
![]() $n,k$
, essential fixed point classes of
$n,k$
, essential fixed point classes of
![]() $f^{kn}$
can only reduce to essential fixed point classes of
$f^{kn}$
can only reduce to essential fixed point classes of
![]() $f^{k}$
. A space
$f^{k}$
. A space
![]() $X$
is called essentially reducible if every self-map
$X$
is called essentially reducible if every self-map
![]() $f:X\rightarrow X$
is essentially reducible.
$f:X\rightarrow X$
is essentially reducible.
It can be shown that the fixed point classes for maps on infra-nilmanifolds always have this nice structure for their boosting and reducing relations.
Theorem 2.5. [Reference Lee and Zhao17]
Infra-nilmanifolds are essentially reducible.
One of the consequences of having this property, is the following.
Theorem 2.6. [Reference Alsedà, Baldwin, Llibre, Swanson and Szlenk1]
Suppose that
![]() $f$
is essentially reducible and suppose that
$f$
is essentially reducible and suppose that
then
![]() $k\in \operatorname{HPer}(f)$
.
$k\in \operatorname{HPer}(f)$
.
The idea of this theorem is actually quite easy to grasp. Because maps on infra-nilmanifolds are essentially reducible, every reducible essential fixed point class on level
![]() $k$
will reduce to an essential fixed point class on level
$k$
will reduce to an essential fixed point class on level
![]() $\frac{k}{p}$
, with
$\frac{k}{p}$
, with
![]() $p$
a prime divisor of
$p$
a prime divisor of
![]() $k$
. Therefore, the condition
$k$
. Therefore, the condition
actually tells us that there is definitely one irreducible essential fixed point class on level
![]() $k$
, which means that there is at least one periodic point of pure period
$k$
, which means that there is at least one periodic point of pure period
![]() $k$
.
$k$
.
For this paper, this is all we need to know about Nielsen periodic point theory. More information about Nielsen periodic point theory in general can be found in [Reference Heath and Keppelmann11, Reference Jezierski and Marzantowicz13] or [Reference Jiang14].
3
 $\operatorname{HPer}(f)$
for hyperbolic maps on infra-nilmanifolds
$\operatorname{HPer}(f)$
for hyperbolic maps on infra-nilmanifolds
3.1 The nonnilpotent case
We begin with the following definition, which tells us something about the asymptotic behavior of the sequence
![]() $\left\{N(f^{k})\right\}_{k=1}^{\infty }$
.
$\left\{N(f^{k})\right\}_{k=1}^{\infty }$
.
Definition 3.1. The asymptotic Nielsen number of
![]() $f$
is defined as
$f$
is defined as
By
![]() $\operatorname{sp}(A)$
we mean the spectral radius of the matrix or the operator
$\operatorname{sp}(A)$
we mean the spectral radius of the matrix or the operator
![]() $A$
. It equals the largest modulus of an eigenvalue of
$A$
. It equals the largest modulus of an eigenvalue of
![]() $A$
.
$A$
.
Theorem 3.2. [Reference Fel’shtyn and Lee8, Theorem 4.3]
For a continuous map
![]() $f$
on an infra-nilmanifold, with affine homotopy lift
$f$
on an infra-nilmanifold, with affine homotopy lift
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
, such that
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
, such that
![]() $\mathfrak{D}_{\ast }$
has no eigenvalue
$\mathfrak{D}_{\ast }$
has no eigenvalue
![]() $1$
, we have
$1$
, we have
If
![]() $\{\unicode[STIX]{x1D708}_{i}\}_{i\in I}$
is the set of eigenvalues of
$\{\unicode[STIX]{x1D708}_{i}\}_{i\in I}$
is the set of eigenvalues of
![]() $\mathfrak{D}_{\ast }$
, we know that
$\mathfrak{D}_{\ast }$
, we know that
Therefore, we have the following corollary of Theorem 3.2.
Corollary 3.3. Let
![]() $f$
be a hyperbolic, continuous map on an infra-nilmanifold. Let
$f$
be a hyperbolic, continuous map on an infra-nilmanifold. Let
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
be an affine homotopy lift of
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
be an affine homotopy lift of
![]() $f$
and let
$f$
and let
![]() $\{\unicode[STIX]{x1D708}_{i}\}_{i\in I}$
be the set of eigenvalues of
$\{\unicode[STIX]{x1D708}_{i}\}_{i\in I}$
be the set of eigenvalues of
![]() $\mathfrak{D}_{\ast }$
. If
$\mathfrak{D}_{\ast }$
. If
![]() $\mathfrak{D}_{\ast }$
is not nilpotent, then
$\mathfrak{D}_{\ast }$
is not nilpotent, then
Proof. When
![]() $\mathfrak{D}_{\ast }$
is not nilpotent, we know by Remark 1.6 that
$\mathfrak{D}_{\ast }$
is not nilpotent, we know by Remark 1.6 that
![]() $\operatorname{sp}(\mathfrak{D}_{\ast })>1$
. Because
$\operatorname{sp}(\mathfrak{D}_{\ast })>1$
. Because
![]() $f$
is hyperbolic,
$f$
is hyperbolic,
![]() $1$
is certainly not an eigenvalue of
$1$
is certainly not an eigenvalue of
![]() $\mathfrak{D}_{\ast }$
and therefore, we can use the result of Theorem 3.2.◻
$\mathfrak{D}_{\ast }$
and therefore, we can use the result of Theorem 3.2.◻
Because of Theorem 2.2, we know that
![]() $N_{f}(z)$
can be written as the quotient of Lefschetz zeta functions. Since every Lefschetz zeta function on a compact polyhedron is of the form
$N_{f}(z)$
can be written as the quotient of Lefschetz zeta functions. Since every Lefschetz zeta function on a compact polyhedron is of the form
with
![]() $\unicode[STIX]{x1D707}_{i}\in \mathbb{C}$
and
$\unicode[STIX]{x1D707}_{i}\in \mathbb{C}$
and
![]() $\unicode[STIX]{x1D6FE}_{i}\in \{1,-1\}$
, the same will hold for
$\unicode[STIX]{x1D6FE}_{i}\in \{1,-1\}$
, the same will hold for
![]() $N_{f}(z)$
. Also, it is easy to check that
$N_{f}(z)$
. Also, it is easy to check that
for all
![]() $k\in \mathbb{N}$
.
$k\in \mathbb{N}$
.
In Remark 2.1 we already mentioned the fact that for nilmanifolds the
![]() $\unicode[STIX]{x1D707}_{i}$
’s appearing in the expression for
$\unicode[STIX]{x1D707}_{i}$
’s appearing in the expression for
![]() $L_{f}(z)$
are eigenvalues of
$L_{f}(z)$
are eigenvalues of
![]() $\bigwedge \mathfrak{D}_{\ast }$
. We now claim that the same holds for maps on infra-nilmanifolds. Consider an infra-nilmanifold
$\bigwedge \mathfrak{D}_{\ast }$
. We now claim that the same holds for maps on infra-nilmanifolds. Consider an infra-nilmanifold
![]() $\unicode[STIX]{x1D6E4}\backslash G$
and a self-map
$\unicode[STIX]{x1D6E4}\backslash G$
and a self-map
![]() $f$
of
$f$
of
![]() $\unicode[STIX]{x1D6E4}\backslash G$
with affine homotopy lift
$\unicode[STIX]{x1D6E4}\backslash G$
with affine homotopy lift
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
. Without loss of generality, we may assume that
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
. Without loss of generality, we may assume that
![]() $f=\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}$
. We now fix a fully characteristic subgroup
$f=\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}$
. We now fix a fully characteristic subgroup
![]() $\unicode[STIX]{x1D6EC}$
of finite index in
$\unicode[STIX]{x1D6EC}$
of finite index in
![]() $\unicode[STIX]{x1D6E4}$
that is contained in
$\unicode[STIX]{x1D6E4}$
that is contained in
![]() $G$
(e.g., see [Reference Lee and Lee16]). Hence for the induced morphism
$G$
(e.g., see [Reference Lee and Lee16]). Hence for the induced morphism
![]() $f_{\ast }:\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}$
we have that
$f_{\ast }:\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}$
we have that
![]() $f_{\ast }(\unicode[STIX]{x1D6EC})\subseteq \unicode[STIX]{x1D6EC}$
. It follows that
$f_{\ast }(\unicode[STIX]{x1D6EC})\subseteq \unicode[STIX]{x1D6EC}$
. It follows that
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
also induces a map
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
also induces a map
![]() $\hat{f}$
on the nilmanifold
$\hat{f}$
on the nilmanifold
![]() $\unicode[STIX]{x1D6EC}\backslash G$
and that
$\unicode[STIX]{x1D6EC}\backslash G$
and that
![]() $\hat{f}_{\ast }=f_{\ast |\unicode[STIX]{x1D6EC}}$
. By [Reference Brown2, Theorem III 10.4] we know that the restriction map induces an isomorphism
$\hat{f}_{\ast }=f_{\ast |\unicode[STIX]{x1D6EC}}$
. By [Reference Brown2, Theorem III 10.4] we know that the restriction map induces an isomorphism
![]() $\text{res}:H^{i}(\unicode[STIX]{x1D6E4},\mathbb{Q})\rightarrow H^{i}(\unicode[STIX]{x1D6EC},\mathbb{Q})^{\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6EC}}$
. As the restriction map is natural, we obtain the following commutative diagram:
$\text{res}:H^{i}(\unicode[STIX]{x1D6E4},\mathbb{Q})\rightarrow H^{i}(\unicode[STIX]{x1D6EC},\mathbb{Q})^{\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6EC}}$
. As the restriction map is natural, we obtain the following commutative diagram:

It follows that each of the eigenvalues of
![]() $f_{\ast }^{i}$
is also an eigenvalue of
$f_{\ast }^{i}$
is also an eigenvalue of
![]() $\hat{f}_{\ast }^{i}$
. Since the latter ones are all eigenvalues of
$\hat{f}_{\ast }^{i}$
. Since the latter ones are all eigenvalues of
![]() $\bigwedge ^{i}\mathfrak{D}_{\ast }$
, by Remark 2.1, it follows that all eigenvalues of
$\bigwedge ^{i}\mathfrak{D}_{\ast }$
, by Remark 2.1, it follows that all eigenvalues of
![]() $f_{\ast }^{i}$
are also eigenvalues of
$f_{\ast }^{i}$
are also eigenvalues of
![]() $\bigwedge ^{i}\mathfrak{D}_{\ast }$
. This means that the
$\bigwedge ^{i}\mathfrak{D}_{\ast }$
. This means that the
![]() $\unicode[STIX]{x1D707}_{i}$
’s appearing in the expression for
$\unicode[STIX]{x1D707}_{i}$
’s appearing in the expression for
![]() $L_{f}(z)$
are eigenvalues of
$L_{f}(z)$
are eigenvalues of
![]() $\bigwedge \mathfrak{D}_{\ast }$
and of course, because
$\bigwedge \mathfrak{D}_{\ast }$
and of course, because
![]() $f_{+}$
has the same affine homotopy lift as
$f_{+}$
has the same affine homotopy lift as
![]() $f$
, the same applies to
$f$
, the same applies to
![]() $L_{f_{+}}(z)$
.
$L_{f_{+}}(z)$
.
By Theorem 2.2, we know that
![]() $N_{f}(z)$
can be written as a combination of
$N_{f}(z)$
can be written as a combination of
![]() $L_{f}(z)$
and possibly
$L_{f}(z)$
and possibly
![]() $L_{f_{+}}(z)$
, or as a combination of
$L_{f_{+}}(z)$
, or as a combination of
![]() $L_{f}(-z)$
and possibly
$L_{f}(-z)$
and possibly
![]() $L_{f_{+}}(-z)$
. In the first case, by the previous discussion we see that all
$L_{f_{+}}(-z)$
. In the first case, by the previous discussion we see that all
![]() $\unicode[STIX]{x1D706}_{i}$
’s in the expression for
$\unicode[STIX]{x1D706}_{i}$
’s in the expression for
![]() $N_{f}(z)$
are eigenvalues of
$N_{f}(z)$
are eigenvalues of
![]() $\bigwedge \mathfrak{D}_{\ast }$
. In the latter case, all
$\bigwedge \mathfrak{D}_{\ast }$
. In the latter case, all
![]() $\unicode[STIX]{x1D706}_{i}$
’s are the opposite of eigenvalues of
$\unicode[STIX]{x1D706}_{i}$
’s are the opposite of eigenvalues of
![]() $\bigwedge \mathfrak{D}_{\ast }$
. This means that we can write
$\bigwedge \mathfrak{D}_{\ast }$
. This means that we can write
such that all
![]() $\unicode[STIX]{x1D706}_{i}$
’s or all
$\unicode[STIX]{x1D706}_{i}$
’s or all
![]() $-\unicode[STIX]{x1D706}_{i}$
’s are eigenvalues of
$-\unicode[STIX]{x1D706}_{i}$
’s are eigenvalues of
![]() $\bigwedge \mathfrak{D}_{\ast }$
.
$\bigwedge \mathfrak{D}_{\ast }$
.
Lemma 3.4. If
![]() $f$
is a nonnilpotent hyperbolic map on an infra-nilmanifold, with
$f$
is a nonnilpotent hyperbolic map on an infra-nilmanifold, with
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
as affine homotopy lift, it is possible to write
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
as affine homotopy lift, it is possible to write
with
![]() $a_{i}\in \mathbb{Z}$
,
$a_{i}\in \mathbb{Z}$
,
![]() $a_{1}\geqslant 1$
and such that
$a_{1}\geqslant 1$
and such that
Proof. By previous arguments, we know that it is possible to write
where all
![]() $\unicode[STIX]{x1D706}_{i}$
’s or all
$\unicode[STIX]{x1D706}_{i}$
’s or all
![]() $-\unicode[STIX]{x1D706}_{i}$
’s are eigenvalues of
$-\unicode[STIX]{x1D706}_{i}$
’s are eigenvalues of
![]() $\bigwedge \mathfrak{D}_{\ast }$
. By grouping the
$\bigwedge \mathfrak{D}_{\ast }$
. By grouping the
![]() $\unicode[STIX]{x1D706}$
’s that appear more than once and by changing the order, we obtain the desired form
$\unicode[STIX]{x1D706}$
’s that appear more than once and by changing the order, we obtain the desired form
with
![]() $a_{i}\in \mathbb{Z}$
and
$a_{i}\in \mathbb{Z}$
and
![]() $|\unicode[STIX]{x1D706}_{1}|\geqslant |\unicode[STIX]{x1D706}_{2}|\geqslant \ldots \geqslant |\unicode[STIX]{x1D706}_{m}|.$
There is a unique eigenvalue of
$|\unicode[STIX]{x1D706}_{1}|\geqslant |\unicode[STIX]{x1D706}_{2}|\geqslant \ldots \geqslant |\unicode[STIX]{x1D706}_{m}|.$
There is a unique eigenvalue of
![]() $\bigwedge \mathfrak{D}_{\ast }$
of maximal modulus, namely the product
$\bigwedge \mathfrak{D}_{\ast }$
of maximal modulus, namely the product
Note that the product is real, because for every
![]() $\unicode[STIX]{x1D706}\not \in \mathbb{R}$
, we know that if
$\unicode[STIX]{x1D706}\not \in \mathbb{R}$
, we know that if
![]() $|\unicode[STIX]{x1D706}|>1$
, then
$|\unicode[STIX]{x1D706}|>1$
, then
![]() $|\overline{\unicode[STIX]{x1D706}}|>1$
and both are eigenvalues of
$|\overline{\unicode[STIX]{x1D706}}|>1$
and both are eigenvalues of
![]() $\bigwedge \mathfrak{D}_{\ast }$
, because
$\bigwedge \mathfrak{D}_{\ast }$
, because
![]() $\mathfrak{D}_{\ast }$
is a real matrix. It is unique because
$\mathfrak{D}_{\ast }$
is a real matrix. It is unique because
![]() $f$
is hyperbolic and
$f$
is hyperbolic and
![]() $\mathfrak{D}_{\ast }$
has no eigenvalues of modulus
$\mathfrak{D}_{\ast }$
has no eigenvalues of modulus
![]() $1$
.
$1$
.
Because of Theorem 3.2, we know that
![]() $N^{\infty }(f)=\operatorname{sp}(\bigwedge \mathfrak{D}_{\ast })=|\unicode[STIX]{x1D707}_{1}|$
. Suppose now that
$N^{\infty }(f)=\operatorname{sp}(\bigwedge \mathfrak{D}_{\ast })=|\unicode[STIX]{x1D707}_{1}|$
. Suppose now that
![]() $\unicode[STIX]{x1D707}_{1}$
or
$\unicode[STIX]{x1D707}_{1}$
or
![]() $-\unicode[STIX]{x1D707}_{1}$
does not appear as one of the
$-\unicode[STIX]{x1D707}_{1}$
does not appear as one of the
![]() $\unicode[STIX]{x1D706}$
’s in the expression of
$\unicode[STIX]{x1D706}$
’s in the expression of
![]() $N(f^{k})$
. Then, it should still hold that
$N(f^{k})$
. Then, it should still hold that
Let
![]() $a_{\max }=\max \{|a_{i}|\}$
, then it is easy to derive that for all
$a_{\max }=\max \{|a_{i}|\}$
, then it is easy to derive that for all
![]() $k$
:
$k$
:
So, we would have that
 $$\begin{eqnarray}1\leqslant \limsup _{k\rightarrow \infty }\left(ma_{\max }\left|\frac{\unicode[STIX]{x1D706}_{1}}{\unicode[STIX]{x1D707}_{1}}\right|^{k}\right)^{1/k}=\left|\frac{\unicode[STIX]{x1D706}_{1}}{\unicode[STIX]{x1D707}_{1}}\right|<1,\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant \limsup _{k\rightarrow \infty }\left(ma_{\max }\left|\frac{\unicode[STIX]{x1D706}_{1}}{\unicode[STIX]{x1D707}_{1}}\right|^{k}\right)^{1/k}=\left|\frac{\unicode[STIX]{x1D706}_{1}}{\unicode[STIX]{x1D707}_{1}}\right|<1,\end{eqnarray}$$
where the last inequality follows from the fact that
![]() $\unicode[STIX]{x1D707}_{1}$
is the unique eigenvalue of maximal modulus. Moreover, an easy argument shows that
$\unicode[STIX]{x1D707}_{1}$
is the unique eigenvalue of maximal modulus. Moreover, an easy argument shows that
![]() $a_{1}<0$
or
$a_{1}<0$
or
![]() $\unicode[STIX]{x1D706}_{1}<0$
cannot occur in the expression of
$\unicode[STIX]{x1D706}_{1}<0$
cannot occur in the expression of
![]() $N(f^{k})$
, because otherwise
$N(f^{k})$
, because otherwise
![]() $N(f^{k})$
would be negative for sufficiently large
$N(f^{k})$
would be negative for sufficiently large
![]() $k$
. As we have already proved that
$k$
. As we have already proved that
![]() $a_{1}=0$
is impossible, we know that
$a_{1}=0$
is impossible, we know that
![]() $a_{1}\geqslant 1$
and that
$a_{1}\geqslant 1$
and that
![]() $\operatorname{sp}(\bigwedge \mathfrak{D}_{\ast })$
will appear as one of the
$\operatorname{sp}(\bigwedge \mathfrak{D}_{\ast })$
will appear as one of the
![]() $\unicode[STIX]{x1D706}$
’s in the expression for
$\unicode[STIX]{x1D706}$
’s in the expression for
![]() $N(f^{k})$
.◻
$N(f^{k})$
.◻
Remark 3.5. The fact that
![]() $\operatorname{sp}(\bigwedge \mathfrak{D}_{\ast })$
has to appear in the expression for
$\operatorname{sp}(\bigwedge \mathfrak{D}_{\ast })$
has to appear in the expression for
![]() $N(f^{k})$
was proved in a more general setting in [Reference Fel’shtyn and Lee9].
$N(f^{k})$
was proved in a more general setting in [Reference Fel’shtyn and Lee9].
Lemma 3.6. If
![]() $f$
is a hyperbolic map on an infra-nilmanifold, then
$f$
is a hyperbolic map on an infra-nilmanifold, then
![]() $N(f^{k})\neq 0$
for all
$N(f^{k})\neq 0$
for all
![]() $k>0$
.
$k>0$
.
Proof. Let
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
be an affine homotopy lift of
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
be an affine homotopy lift of
![]() $f$
and let
$f$
and let
![]() $F$
be the holonomy group of the infra–nilmanifold. By [Reference Lee and Lee16], we know that
$F$
be the holonomy group of the infra–nilmanifold. By [Reference Lee and Lee16], we know that
Because all the terms make a nonnegative contribution to this sum, we know that
where the
![]() $\unicode[STIX]{x1D707}_{i}$
are all the eigenvalues of
$\unicode[STIX]{x1D707}_{i}$
are all the eigenvalues of
![]() $\mathfrak{D}_{\ast }$
. The last inequality follows from the fact that
$\mathfrak{D}_{\ast }$
. The last inequality follows from the fact that
![]() $f$
is hyperbolic and so there are no eigenvalues of modulus
$f$
is hyperbolic and so there are no eigenvalues of modulus
![]() $1$
.◻
$1$
.◻
From now on, we consider
![]() $f$
to be a hyperbolic map on an infra-nilmanifold and
$f$
to be a hyperbolic map on an infra-nilmanifold and
![]() $N(f^{k})$
to be of the form
$N(f^{k})$
to be of the form
with
![]() $a_{i}\in \mathbb{Z}$
,
$a_{i}\in \mathbb{Z}$
,
![]() $a_{1}\geqslant 1$
and such that
$a_{1}\geqslant 1$
and such that
For the sake of clarity, we keep using this notation in the rest of this paragraph.
Lemma 3.7. For all
![]() $\unicode[STIX]{x1D707}$
such that
$\unicode[STIX]{x1D707}$
such that
![]() $\unicode[STIX]{x1D706}_{1}>\unicode[STIX]{x1D707}>1$
, there exists
$\unicode[STIX]{x1D706}_{1}>\unicode[STIX]{x1D707}>1$
, there exists
![]() $k_{0}\in \mathbb{N}$
, such that for all
$k_{0}\in \mathbb{N}$
, such that for all
![]() $k\geqslant k_{0}$
and for all
$k\geqslant k_{0}$
and for all
![]() $n\in \mathbb{N}$
, we have the following inequality:
$n\in \mathbb{N}$
, we have the following inequality:
Proof. Let
![]() $1>\unicode[STIX]{x1D700}>0$
, such that
$1>\unicode[STIX]{x1D700}>0$
, such that
Note that this implies that
Now, choose
![]() $k_{0}\in \mathbb{N}$
such that, for all
$k_{0}\in \mathbb{N}$
such that, for all
![]() $i\in \{2,\ldots ,m\}$
,
$i\in \{2,\ldots ,m\}$
,
Because of Lemma 3.4, we know that
![]() $|\unicode[STIX]{x1D706}_{1}|>|\unicode[STIX]{x1D706}_{i}|$
, for all these
$|\unicode[STIX]{x1D706}_{1}|>|\unicode[STIX]{x1D706}_{i}|$
, for all these
![]() $i$
’s, so the inequality will hold for
$i$
’s, so the inequality will hold for
![]() $k_{0}$
sufficiently large.
$k_{0}$
sufficiently large.
Now, consider the fraction
 $$\begin{eqnarray}\frac{N(f^{k+n})}{N(f^{k})}=\frac{a_{1}\unicode[STIX]{x1D706}_{1}^{k+n}+\mathop{\sum }_{i=2}^{m}a_{i}\unicode[STIX]{x1D706}_{i}^{k+n}}{a_{1}\unicode[STIX]{x1D706}_{1}^{k}+\mathop{\sum }_{i=2}^{m}a_{i}\unicode[STIX]{x1D706}_{i}^{k}}=\frac{\unicode[STIX]{x1D706}_{1}^{n}+\mathop{\sum }_{i=2}^{m}\frac{a_{i}}{a_{1}}\frac{\unicode[STIX]{x1D706}_{i}}{\unicode[STIX]{x1D706}_{1}}^{k}\unicode[STIX]{x1D706}_{i}^{n}}{1+\displaystyle \mathop{\sum }_{i=2}^{m}\frac{a_{i}}{a_{1}}\frac{\unicode[STIX]{x1D706}_{i}}{\unicode[STIX]{x1D706}_{1}}^{k}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{N(f^{k+n})}{N(f^{k})}=\frac{a_{1}\unicode[STIX]{x1D706}_{1}^{k+n}+\mathop{\sum }_{i=2}^{m}a_{i}\unicode[STIX]{x1D706}_{i}^{k+n}}{a_{1}\unicode[STIX]{x1D706}_{1}^{k}+\mathop{\sum }_{i=2}^{m}a_{i}\unicode[STIX]{x1D706}_{i}^{k}}=\frac{\unicode[STIX]{x1D706}_{1}^{n}+\mathop{\sum }_{i=2}^{m}\frac{a_{i}}{a_{1}}\frac{\unicode[STIX]{x1D706}_{i}}{\unicode[STIX]{x1D706}_{1}}^{k}\unicode[STIX]{x1D706}_{i}^{n}}{1+\displaystyle \mathop{\sum }_{i=2}^{m}\frac{a_{i}}{a_{1}}\frac{\unicode[STIX]{x1D706}_{i}}{\unicode[STIX]{x1D706}_{1}}^{k}}.\end{eqnarray}$$
Note that
![]() $N(f^{k})\neq 0$
, according to Lemma 3.6, so the fraction is well defined. It is now easy to see that this equality implies the following inequalities:
$N(f^{k})\neq 0$
, according to Lemma 3.6, so the fraction is well defined. It is now easy to see that this equality implies the following inequalities:
 $$\begin{eqnarray}\frac{N(f^{k+n})}{N(f^{k})}\geqslant \frac{\unicode[STIX]{x1D706}_{1}^{n}-\left|\mathop{\sum }_{i=2}^{m}\frac{a_{i}}{a_{1}}\frac{\unicode[STIX]{x1D706}_{i}}{\unicode[STIX]{x1D706}_{1}}^{k}\right|\unicode[STIX]{x1D706}_{1}^{n}}{1+\left|\mathop{\sum }_{i=2}^{m}\frac{a_{i}}{a_{1}}\frac{\unicode[STIX]{x1D706}_{i}}{\unicode[STIX]{x1D706}_{1}}^{k}\right|}>\unicode[STIX]{x1D706}_{1}^{n}\frac{1-\unicode[STIX]{x1D700}}{1+\unicode[STIX]{x1D700}}\geqslant \unicode[STIX]{x1D706}_{1}^{n}\left(\frac{1-\unicode[STIX]{x1D700}}{1+\unicode[STIX]{x1D700}}\right)^{n}\geqslant \unicode[STIX]{x1D707}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{N(f^{k+n})}{N(f^{k})}\geqslant \frac{\unicode[STIX]{x1D706}_{1}^{n}-\left|\mathop{\sum }_{i=2}^{m}\frac{a_{i}}{a_{1}}\frac{\unicode[STIX]{x1D706}_{i}}{\unicode[STIX]{x1D706}_{1}}^{k}\right|\unicode[STIX]{x1D706}_{1}^{n}}{1+\left|\mathop{\sum }_{i=2}^{m}\frac{a_{i}}{a_{1}}\frac{\unicode[STIX]{x1D706}_{i}}{\unicode[STIX]{x1D706}_{1}}^{k}\right|}>\unicode[STIX]{x1D706}_{1}^{n}\frac{1-\unicode[STIX]{x1D700}}{1+\unicode[STIX]{x1D700}}\geqslant \unicode[STIX]{x1D706}_{1}^{n}\left(\frac{1-\unicode[STIX]{x1D700}}{1+\unicode[STIX]{x1D700}}\right)^{n}\geqslant \unicode[STIX]{x1D707}^{n}.\end{eqnarray}$$
◻
Corollary 3.8. There exists
![]() $\unicode[STIX]{x1D708}$
, such that
$\unicode[STIX]{x1D708}$
, such that
![]() $\unicode[STIX]{x1D706}_{1}>\unicode[STIX]{x1D708}>1$
and an
$\unicode[STIX]{x1D706}_{1}>\unicode[STIX]{x1D708}>1$
and an
![]() $l_{0}\in \mathbb{N}$
, such that for all
$l_{0}\in \mathbb{N}$
, such that for all
![]() $l\geqslant l_{0}$
and for all
$l\geqslant l_{0}$
and for all
![]() $k<l$
:
$k<l$
:
Proof. Fix
![]() $\unicode[STIX]{x1D707}$
as in Lemma 3.7 and let
$\unicode[STIX]{x1D707}$
as in Lemma 3.7 and let
![]() $k_{0}$
be the resulting integer from this lemma. Note that Lemma 3.7 actually tells us that the sequence
$k_{0}$
be the resulting integer from this lemma. Note that Lemma 3.7 actually tells us that the sequence
![]() $\{N(f^{k})\}_{k=1}^{\infty }$
will be strictly increasing from a certain point onwards. Because all Nielsen numbers are integers, this means that there will exist
$\{N(f^{k})\}_{k=1}^{\infty }$
will be strictly increasing from a certain point onwards. Because all Nielsen numbers are integers, this means that there will exist
![]() $l_{0}\geqslant k_{0}$
, such that
$l_{0}\geqslant k_{0}$
, such that
![]() $N(f^{l_{0}})>N(f^{l})$
, for all
$N(f^{l_{0}})>N(f^{l})$
, for all
![]() $l<l_{0}$
, so also for all
$l<l_{0}$
, so also for all
![]() $l<k_{0}$
.
$l<k_{0}$
.
Now, let us define the following number
It is clear that
![]() $\unicode[STIX]{x1D70F}>1$
. Let
$\unicode[STIX]{x1D70F}>1$
. Let
![]() $\unicode[STIX]{x1D708}=\min \left\{\unicode[STIX]{x1D707},(1+\unicode[STIX]{x1D70F})/2\right\}$
. Clearly,
$\unicode[STIX]{x1D708}=\min \left\{\unicode[STIX]{x1D707},(1+\unicode[STIX]{x1D70F})/2\right\}$
. Clearly,
![]() $\unicode[STIX]{x1D706}_{1}>\unicode[STIX]{x1D708}>1$
and, for all
$\unicode[STIX]{x1D706}_{1}>\unicode[STIX]{x1D708}>1$
and, for all
![]() $k<l_{0}$
, we have the following inequalities:
$k<l_{0}$
, we have the following inequalities:
Because of Lemma 3.7 and the fact that
![]() $\unicode[STIX]{x1D707}\geqslant \unicode[STIX]{x1D708}$
, we know this inequality also applies to all
$\unicode[STIX]{x1D707}\geqslant \unicode[STIX]{x1D708}$
, we know this inequality also applies to all
![]() $l\geqslant l_{0}$
.◻
$l\geqslant l_{0}$
.◻
Theorem 3.9. If
![]() $f$
is a hyperbolic map on an infra-nilmanifold, with affine homotopy lift
$f$
is a hyperbolic map on an infra-nilmanifold, with affine homotopy lift
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
, such that
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
, such that
![]() $\mathfrak{D}_{\ast }$
is not nilpotent, then there exists an integer
$\mathfrak{D}_{\ast }$
is not nilpotent, then there exists an integer
![]() $m_{0}$
, such that
$m_{0}$
, such that
Proof. Choose
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $l_{0}$
as in Corollary 3.8. Since
$l_{0}$
as in Corollary 3.8. Since
we know there exists a
![]() $k_{0}$
, such that
$k_{0}$
, such that
![]() $\unicode[STIX]{x1D708}^{2^{k-1}}>k$
for all
$\unicode[STIX]{x1D708}^{2^{k-1}}>k$
for all
![]() $k\geqslant k_{0}$
. Define
$k\geqslant k_{0}$
. Define
![]() $m_{0}=\max \{2^{k_{0}},2l_{0}+1\}$
.
$m_{0}=\max \{2^{k_{0}},2l_{0}+1\}$
.
Now, suppose that
![]() $m\geqslant m_{0}$
and
$m\geqslant m_{0}$
and
![]() $m$
is even. Let
$m$
is even. Let
![]() $K$
denote the number of different prime divisors of
$K$
denote the number of different prime divisors of
![]() $m$
. As
$m$
. As
![]() $m\geqslant 2l_{0}+1$
, we know that
$m\geqslant 2l_{0}+1$
, we know that
![]() $m/2>l_{0}$
and hence the result of Corollary 3.8 applies. Therefore, we have the following inequalities
$m/2>l_{0}$
and hence the result of Corollary 3.8 applies. Therefore, we have the following inequalities
By Theorem 2.6, it now suffices to show that
Because
![]() $K$
denotes the number of different prime divisors of
$K$
denotes the number of different prime divisors of
![]() $m$
, we certainly know that
$m$
, we certainly know that
![]() $m>2^{K}$
. By the definition of
$m>2^{K}$
. By the definition of
![]() $m_{0}$
, we also know that
$m_{0}$
, we also know that
![]() $m\geqslant 2^{k_{0}}$
. If
$m\geqslant 2^{k_{0}}$
. If
![]() $K\geqslant k_{0}$
, then
$K\geqslant k_{0}$
, then
which is sufficient. If
![]() $k_{0}>K$
, we have that
$k_{0}>K$
, we have that
So, when
![]() $m\geqslant m_{0}$
is even,
$m\geqslant m_{0}$
is even,
![]() $m\in \operatorname{HPer}(f)$
.
$m\in \operatorname{HPer}(f)$
.
When
![]() $m\geqslant m_{0}$
is odd, a similar argument holds. Let
$m\geqslant m_{0}$
is odd, a similar argument holds. Let
![]() $K$
again be the number of different prime divisors of
$K$
again be the number of different prime divisors of
![]() $m$
and note that
$m$
and note that
![]() $m\geqslant 2l_{0}+1$
implies that
$m\geqslant 2l_{0}+1$
implies that
![]() $(m-1)/2\geqslant l_{0}$
. Again, by using Corollary 3.8, we obtain the following inequalities:
$(m-1)/2\geqslant l_{0}$
. Again, by using Corollary 3.8, we obtain the following inequalities:
Again,
![]() $m>2^{K}$
and by definition
$m>2^{K}$
and by definition
![]() $m\geqslant 2^{k_{0}}$
. When
$m\geqslant 2^{k_{0}}$
. When
![]() $K\geqslant k_{0}$
,
$K\geqslant k_{0}$
,
When
![]() $k_{0}>K$
, the same reasoning gives us
$k_{0}>K$
, the same reasoning gives us
This concludes the proof of this theorem. ◻
Remark 3.10. Having obtained Lemma 3.4, it is also possible to prove our main theorem in an alternative way, by following the approach of [Reference Fel’shtyn and Lee8, Section 6].
Remark 3.11. Note that our proof also applies to every essentially irreducible map
![]() $f$
(on any manifold) for which there exists
$f$
(on any manifold) for which there exists
![]() $\unicode[STIX]{x1D707}>1$
and
$\unicode[STIX]{x1D707}>1$
and
![]() $k_{0}\in \mathbb{N}$
, such that for all
$k_{0}\in \mathbb{N}$
, such that for all
![]() $k\geqslant k_{0}$
and for all
$k\geqslant k_{0}$
and for all
![]() $n\in \mathbb{N}$
, we have that
$n\in \mathbb{N}$
, we have that
This condition is therefore sufficient for
![]() $\operatorname{HPer}(f)$
to be cofinite in
$\operatorname{HPer}(f)$
to be cofinite in
![]() $\mathbb{N}$
.
$\mathbb{N}$
.
3.2 The nilpotent case
For the sake of completeness, in this section we also treat the case where
![]() $\mathfrak{D}_{\ast }$
is nilpotent.
$\mathfrak{D}_{\ast }$
is nilpotent.
The following two theorems can be found in [Reference Dekimpe and Penninckx6].
Theorem 3.12. Let
![]() $\unicode[STIX]{x1D6E4}\subseteq \operatorname{Aff}(G)$
be an almost-Bieberbach group with holonomy group
$\unicode[STIX]{x1D6E4}\subseteq \operatorname{Aff}(G)$
be an almost-Bieberbach group with holonomy group
![]() $F\subseteq \operatorname{Aut}(G)$
. Let
$F\subseteq \operatorname{Aut}(G)$
. Let
![]() $M=\unicode[STIX]{x1D6E4}\backslash G$
be the associated infra-nilmanifold. If
$M=\unicode[STIX]{x1D6E4}\backslash G$
be the associated infra-nilmanifold. If
![]() $f:M\rightarrow M$
is a map with affine homotopy lift
$f:M\rightarrow M$
is a map with affine homotopy lift
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
, then
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
, then
Theorem 3.13. Let
![]() $f$
be a map on an infra-nilmanifold such that
$f$
be a map on an infra-nilmanifold such that
![]() $R(f)<\infty$
, then
$R(f)<\infty$
, then
Proposition 3.14. When
![]() $f$
is a hyperbolic map on an infra-nilmanifold with affine homotopy lift
$f$
is a hyperbolic map on an infra-nilmanifold with affine homotopy lift
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
such that
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
such that
![]() $\mathfrak{D}_{\ast }$
is nilpotent then, for all
$\mathfrak{D}_{\ast }$
is nilpotent then, for all
![]() $k$
,
$k$
,
Proof. By combining Theorems 3.12 and 3.13 we know that every fixed point class of
![]() $f^{k}$
is essential if and only if for all
$f^{k}$
is essential if and only if for all
![]() $\mathfrak{A}\in F$
(where
$\mathfrak{A}\in F$
(where
![]() $F$
is the holonomy group of our infra-nilmanifold), it is true that
$F$
is the holonomy group of our infra-nilmanifold), it is true that
By [Reference Dekimpe, De Rock and Malfait4, Lemma 3.1], we know that there exists
![]() $\mathfrak{B}\in F$
, and an integer
$\mathfrak{B}\in F$
, and an integer
![]() $l$
, such that
$l$
, such that
Note that
![]() $\det (I-\mathfrak{B}_{\ast }\mathfrak{D}_{\ast }^{k})=0$
implies that
$\det (I-\mathfrak{B}_{\ast }\mathfrak{D}_{\ast }^{k})=0$
implies that
![]() $\mathfrak{B}_{\ast }\mathfrak{D}_{\ast }^{k}$
has an eigenvalue
$\mathfrak{B}_{\ast }\mathfrak{D}_{\ast }^{k}$
has an eigenvalue
![]() $1$
, but this would mean that
$1$
, but this would mean that
![]() $\mathfrak{D}_{\ast }^{lk}$
has an eigenvalue
$\mathfrak{D}_{\ast }^{lk}$
has an eigenvalue
![]() $1$
, which is in contradiction with the hyperbolicity of our map. Therefore,
$1$
, which is in contradiction with the hyperbolicity of our map. Therefore,
![]() $R(f^{k})=N(f^{k})$
.
$R(f^{k})=N(f^{k})$
.
Note that
![]() $\mathfrak{D}_{\ast }$
only has eigenvalue
$\mathfrak{D}_{\ast }$
only has eigenvalue
![]() $0$
. The fact that there exists
$0$
. The fact that there exists
![]() $\mathfrak{B}\in F$
and an integer
$\mathfrak{B}\in F$
and an integer
![]() $l$
such that
$l$
such that
implies that
![]() $\mathfrak{B}_{\ast }\mathfrak{D}_{\ast }^{k}$
only has eigenvalue
$\mathfrak{B}_{\ast }\mathfrak{D}_{\ast }^{k}$
only has eigenvalue
![]() $0$
. As a consequence
$0$
. As a consequence
for all
![]() $\mathfrak{A}\in F$
. By applying the main formula from [Reference Lee and Lee16], an easy computation shows that
$\mathfrak{A}\in F$
. By applying the main formula from [Reference Lee and Lee16], an easy computation shows that
![]() $N(f^{k})=1$
.◻
$N(f^{k})=1$
.◻
In [Reference Fel’shtyn and Lee8], we find the following proposition.
Proposition 3.15. If
![]() $\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}:M\rightarrow M$
is a continuous map on an infra-nilmanifold, induced by an affine map, then every nonempty fixed point class is path-connected and
$\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}:M\rightarrow M$
is a continuous map on an infra-nilmanifold, induced by an affine map, then every nonempty fixed point class is path-connected and
(1) Every essential fixed point class of
 $\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}$
consists of exactly one point.
$\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}$
consists of exactly one point.(2) Every nonessential fixed point class of
 $\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}$
is empty or consists of infinitely many points.
$\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}$
is empty or consists of infinitely many points.
Theorem 3.16. If
![]() $f$
is a hyperbolic map on an infra-nilmanifold with affine homotopy lift
$f$
is a hyperbolic map on an infra-nilmanifold with affine homotopy lift
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
such that
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
such that
![]() $\mathfrak{D}_{\ast }$
is nilpotent, then
$\mathfrak{D}_{\ast }$
is nilpotent, then
Proof. Let
![]() $\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}$
be the induced map of
$\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}$
be the induced map of
![]() $(\unicode[STIX]{x1D6FF},\mathfrak{D})$
on the infra-nilmanifold. It suffices to show that
$(\unicode[STIX]{x1D6FF},\mathfrak{D})$
on the infra-nilmanifold. It suffices to show that
![]() $\operatorname{Per}(\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})})=\{1\}$
, because
$\operatorname{Per}(\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})})=\{1\}$
, because
![]() $N(f)=1$
immediately implies that
$N(f)=1$
immediately implies that
![]() $1\in \operatorname{HPer}(f)$
.
$1\in \operatorname{HPer}(f)$
.
By Propositions 3.15 and 3.14, we know that
![]() $\operatorname{Fix}(\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}^{k})$
consists of precisely one point, for all
$\operatorname{Fix}(\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}^{k})$
consists of precisely one point, for all
![]() $k>0$
. Because, for all
$k>0$
. Because, for all
![]() $k>0$
, it holds that
$k>0$
, it holds that
we know that
![]() $\operatorname{Fix}(\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}^{k})=\operatorname{Fix}(\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})})$
, for all
$\operatorname{Fix}(\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}^{k})=\operatorname{Fix}(\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})})$
, for all
![]() $k>0$
. From this, it follows that
$k>0$
. From this, it follows that
![]() $\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}$
only has periodic points of pure period
$\overline{(\unicode[STIX]{x1D6FF},\mathfrak{D})}$
only has periodic points of pure period
![]() $1$
.◻
$1$
.◻
Acknowledgments
The authors would like to thank the referee for his/her careful reading of the manuscript and the many helpful suggestions.