Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T23:16:13.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Homotopy groups of pullbacks of varieties

Published online by Cambridge University Press:  22 January 2016

Andrew John Sommese  and
A. van de Ven
Andrew John Sommese
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, Indiana 46556, U.S.A.
A. van de Ven
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, Indiana 46556, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

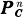In [2, § 9] there is a general result of Fulton and Lazarsfeld relating the homotopy groups of a subvariety of in a certain range of dimensions with those of its pullback under a holomorphic map in the corresponding range of dimensions. It is asked in [2, § 10] whether here is a corresponding result with 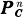replaced by a general rational homogeneous manifold, Y, and with the range of dimensions alluded to above shifted by the ampleness of the holomorphic tangent bundle of Y in the sense of [4]. In this paper we use the techniques of [4, 5, 6, 7] to answer this question in the affirmative.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 102 , June 1986 , pp. 79 - 90
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1986

References

[ 1 ] Faltings, G., Formale Geometrie und homogene Raume, Invent. Math., 64 (1981), 123–165.Google Scholar
[ 2 ] Fulton, W. and Lazarsfeld, R., Connectivity and its applications in algebraic geometry, Lecture Notes in Mathematics, 862 (1981), 26–92 Springer-Verlag, New York.Google Scholar
[ 3 ] Goldstein, N., Ampleness and connectedness in complex G/P , Trans. Amer. Math. Soc., 274 (1982), 361–373.Google Scholar
[ 4 ] Sommese, A. J., Submanifolds of Abelian varieties, Math. Ann., 233 (1978), 229256.Google Scholar
[ 5 ] Sommese, A. J., Concavity theorems, Math. Ann., 235 (1978), 37–53.Google Scholar
[ 6 ] Sommese, A. J., Complex subspaces of homogeneous complex manifolds II-Homotopy results, Nagoya Math. J., 86 (1982), 101–129.Google Scholar
[ 7 ] Sommese, A. J., A convexity theorem, Proceedings of Symposia in Pure Math., 40 (1983), Part 2, 497–505.Google Scholar