Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-19T19:59:32.456Z Has data issue: false hasContentIssue false
  • English
  • Français

Homogeneous line bundles over a toroidal group

Published online by Cambridge University Press:  22 January 2016

Yukitaka Abe
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A connected complex Lie group without non-constant holomorphic functions is called a toroidal group ([5]) or an (H, C)-group ([9]). Let X be an n-dimensional toroidal group. Since a toroidal group is commutative ([5], [9] and [10]), X is isomorphic to the quotient group Cn/Γ by a lattice of Cn. A complex torus is a compact toroidal group. Cousin first studied a non-compact toroidal group ([2]).

Let L be a holomorphic line bundle over X. L is said to be homogeneous if 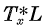is isomorphic to L for all x ε X, where Tx is the translation defined by x ε X. It is well-known that if X is a complex torus, then the following assertions are equivalent:

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 116 , December 1989 , pp. 17 - 24
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1989

References

[1] Abe, Y., (H,C)-groups with positive line bundles, Nagoya Math. J., 107 (1987), 1–11. (in press)Google Scholar
[2] Cousin, P., Sur les fonctions triplement périodiques de deux variables, Acta Math., 1–11.Google Scholar
[3] Kazama, H., ∂ Cohomology of (H,C)-groups, Publ. R.I.M.S. Kyoto Univ., 20 (1984), 297–317.Google Scholar
[4] Kazama, H. and Umeno, T., Complex abelian Lie groups with finite-dimensional cohomology groups, J. Math. Soc. Japan, 36 (1984), 91–106.Google Scholar
[5] Kopfermann, K., Maximale Untergruppen Abelscher komplexer Liescher Gruppen, Schr. Math. Inst. Univ. Munster, 29 (1964).Google Scholar
[6] Malgrange, B., La cohomologie d’une variété analytique complexe à bord pseudoconvexe n’est pas nécessairement séparée, C.R. Acad. Sci. Paris Sér. A, 280 (1975), 93–95.Google Scholar
[7] Matsushima, Y., Fibres holomorphes sur une tore complexe, Nagoya Math. J., 14 (1959), 1–14.Google Scholar
[8] Morimoto, A., Sur la classification des espaces fibres vectories holomorphes surune tore complexe admettant des connexions holomorphes, Nagoya Math. J., 15 (1959), 83–154.Google Scholar
[9] Morimoto, A., Non-compact complex Lie groups without non-constant holomorphic functions, Proc. Conf. on Complex Analysis (Minneapolis 1964), Springer, 1965, 256–272.Google Scholar
[10] Morimoto, A., On the classification of non-compact complex abelian Lie groups, Trans. Amer. Math. Soc, 123 (1966), 200–228.CrossRefGoogle Scholar
[11] Vogt, Ch., Line bundles on toroidal groups, J. Reine Angew. Math., 335 (1982), 197–215.Google Scholar
[12] Vogt, Ch., Two remarks concerning toroidal groups, Manuscripta Math., 41 (1983), 217–232.Google Scholar