Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T00:16:04.304Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGHER CODIMENSIONAL UEDA THEORY FOR A COMPACT SUBMANIFOLD WITH UNITARY FLAT NORMAL BUNDLE

Part of: Compact analytic spaces Cycles and subschemes

Published online by Cambridge University Press:  13 June 2018

TAKAYUKI KOIKE
TAKAYUKI KOIKE*
Affiliation:
Department of Mathematics, Graduate School of Science, Osaka City University, 3-3-138, Sugimoto, Sumiyoshi-ku, Osaka, 558-8585, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $Y$ be a compact complex manifold embedded in a complex manifold with unitary flat normal bundle. Our interest is in a sort of the linearizability problem of a neighborhood of 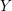$Y$. As a higher codimensional generalization of Ueda’s result, we give a sufficient condition for the existence of a nonsingular holomorphic foliation on a neighborhood of 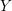$Y$ which includes $Y$ as a leaf with unitary-linear holonomy. We apply this result to the existence problem of a smooth Hermitian metric with semipositive curvature on a nef line bundle.

MSC classification

Primary: 32J25: Transcendental methods of algebraic geometry 14C20: Divisors, linear systems, invertible sheaves
Type
Article
Information
Nagoya Mathematical Journal , Volume 238 , June 2020 , pp. 104 - 136
Copyright
© 2018 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnol’d, V. I., Bifurcations of invariant manifolds of differential equations and normal forms in neighborhoods of elliptic curves, Funkcional Anal. i Prilozen. 10(4) (1976), 1–12; (English translation: Functional Anal. Appl. 10(4) (1977), 249–257).Google Scholar
Brunella, M., On Kähler surfaces with semipositive Ricci curvature, Riv. Mat. Univ. Parma 1 (2010), 441–450.Google Scholar
Demailly, J.-P., Complex analytic and differential geometry, https://www-fourier.ujf-grenoble.fr/∼demailly/manuscripts/agbook.pdf.Google Scholar
Demailly, J.-P., Structure Theorems for Compact Kähler Manifolds with Nef Anticanonical Bundles, Complex Analysis and Geometry, Springer Proceedings in Mathematics & Statistics, 144, Springer, Tokyo, 2015, 119–133.Google Scholar
Fujita, T., Classification Theories of Polarized Varieties, London Mathematical Society Lecture Note Series, 155, Cambridge University Press, Cambridge, 1990.10.1017/CBO9780511662638Google Scholar
Kodaira, K. and Spencer, D. C., A theorem of completeness o f characteristic systems of complete continuous systems, Amer. J. Math. 81 (1959), 477–500.10.2307/2372752Google Scholar
Koike, T., On minimal singular metrics of certain class of line bundles whose section ring is not finitely generated, Ann. Inst. Fourier (Grenoble) 65(5) (2015), 1953–1967.10.5802/aif.2978Google Scholar
Koike, T., Toward a higher codimensional Ueda theory, Math. Z. 281(3) (2015), 967–991.10.1007/s00209-015-1516-6Google Scholar
Koike, T., Ueda theory for compact curves with nodes, Indiana Univ. Math. J. 66(3) (2017), 845–876.10.1512/iumj.2017.66.6038Google Scholar
Koike, T. and Ogawa, N., Local criteria for non embeddability of Levi-flat manifolds, J. Geom. Anal. 28(2) (2018), 1052–1077.10.1007/s12220-017-9853-9Google Scholar
Neeman, A., Ueda theory: theorems and problems, Mem. Amer. Math. Soc. 81(415) (1989), 1–123.Google Scholar
Seshadri, C. S., “Moduli of $\unicode[STIX]{x1D70B}$-vector bundles over an algebraic curve”, in Questions on Algebraic Varieties, C. I. M. E., Varenna 1969, 141–260, Edizioni Cremonese, Roma, 1970.Google Scholar
Siegel, C. L., Iterations of analytic functions, Ann. of Math. 43 (1942), 607–612.10.2307/1968952Google Scholar
Ueda, T., On the neighborhood of a compact complex curve with topologically trivial normal bundle, Math. Kyoto Univ. 22 (1983), 583–607.10.1215/kjm/1250521670Google Scholar