Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hitsuda, Masuyuki
1978.
Measure Theory Applications to Stochastic Analysis.
Vol. 695,
Issue. ,
p.
139.
Prum, Bernard
1984.
Properties of Hida processes on R2. 1. N-Hida processes.
Journal of Multivariate Analysis,
Vol. 15,
Issue. 3,
p.
336.
Mandrekar, V.
and
Thelen, B.
1991.
Stable Processes and Related Topics.
p.
253.
Muraoka, Hiroshi
1992.
Equivalence problems for Gaussian multiple Markov processes and their canonical representations.
Stochastic Processes and their Applications,
Vol. 42,
Issue. 2,
p.
291.
Hibino, Yuji
1993.
The backward canonical representations and interpolations for multiple Markov Gaussian processes.
Stochastic Processes and their Applications,
Vol. 45,
Issue. 1,
p.
29.
Mandal, Pranab K.
and
Mandrekar, V.
2001.
Recent Developments in Infinite-Dimensional Analysis and Quantum Probability.
p.
245.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
1087.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
433.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
795.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
703.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
903.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
217.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
307.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
927.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
961.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
973.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
329.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
125.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
3.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
851.
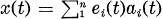
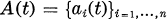 is a Gaussian martingale with
is a Gaussian martingale with

