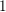Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-04T21:40:21.077Z Has data issue: false hasContentIssue false
  • English
  • Français

HERZ–MORREY SPACES ON THE UNIT BALL WITH VARIABLE EXPONENT APPROACHING $1$ AND DOUBLE PHASE FUNCTIONALS

Part of: Linear function spaces and their duals Harmonic analysis in several variables

Published online by Cambridge University Press:  13 June 2019

YOSHIHIRO MIZUTA ,
TAKAO OHNO Open the ORCID record for TAKAO OHNO [Opens in a new window]  and
TETSU SHIMOMURA
YOSHIHIRO MIZUTA
Affiliation:
4-13-11 Hachi-Hom-Matsu-Minami, Higashi-Hiroshima 739-0144, Japan email [email protected]
TAKAO OHNO
Affiliation:
Faculty of Education, Oita University, Dannoharu Oita-city 870-1192, Japan email [email protected]
TETSU SHIMOMURA
Affiliation:
Department of Mathematics, Graduate School of Education, Hiroshima University, Higashi-Hiroshima 739-8524, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Our aim in this paper is to deal with integrability of maximal functions for Herz–Morrey spaces on the unit ball with variable exponent 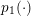$p_{1}(\cdot )$ approaching 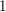$1$ and for double phase functionals 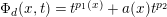$\unicode[STIX]{x1D6F7}_{d}(x,t)=t^{p_{1}(x)}+a(x)t^{p_{2}}$, where 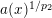$a(x)^{1/p_{2}}$ is nonnegative, bounded and Hölder continuous of order 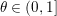$\unicode[STIX]{x1D703}\in (0,1]$ and $1/p_{2}=1-\unicode[STIX]{x1D703}/N>0$. We also establish Sobolev type inequality for Riesz potentials on the unit ball.

MSC classification

Primary: 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.) 42B25: Maximal functions, Littlewood-Paley theory
Type
Article
Information
Nagoya Mathematical Journal , Volume 242 , June 2021 , pp. 1 - 34
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, D. R. and Xiao, J., Morrey spaces in harmonic analysis, Ark. Mat. 50(2) (2012), 201–230.Google Scholar
Almeida, A. and Drihem, D., Maximal, potential and singular type operators on Herz spaces with variable exponents, J. Math. Anal. Appl. 394(2) (2012), 781–795.Google Scholar
Baroni, P., Colombo, M. and Mingione, G., Non-autonomous functionals, borderline cases and related function classes, St Petersburg Math. J. 27 (2016), 347–379.Google Scholar
Burenkov, V. I., Gogatishvili, A., Guliyev, V. S. and Mustafayev, R. Ch., Boundedness of the fractional maximal operator in local Morrey-type spaces, Complex Var. Elliptic Equ. 55(8–10) (2010), 739–758.Google Scholar
Burenkov, V. I., Gogatishvili, A., Guliyev, V. S. and Mustafayev, R. Ch., Boundedness of the Riesz potential in local Morrey-type spaces, Potential Anal. 35(1) (2011), 67–87.Google Scholar
Burenkov, V. I. and Guliyev, H. V., Necessary and sufficient conditions for boundedness of the maximal operator in the local Morrey-type spaces, Stud. Math. 163(2) (2004), 157–176.Google Scholar
Colasuonno, F. and Squassina, M., Eigenvalues for double phase variational integrals, Ann. Mat. Pura Appl. (4) 195(6) (2016), 1917–1959.Google Scholar
Cruz-Uribe, D., Fiorenza, A. and Neugebauer, C. J., The maximal function on variable L p spaces, Ann. Acad. Sci. Fenn. Ser. Math. 28 (2003), 223–238; 29 (2004), 247–249.Google Scholar
Colombo, M. and Mingione, G., Regularity for double phase variational problems, Arch. Ration. Mech. Anal. 215 (2015), 443–496.Google Scholar
Diening, L., Harjulehto, P., Hästö, P. and Růžička, M., Lebesgue and Sobolev spaces With Variable Exponents, Lecture Notes in Mathematics 2017, Springer, Heidelberg, 2011.Google Scholar
Esposito, L., Leonetti, F. and Mingione, G., Sharp regularity for functionals with (p, q) growth, J. Differential Equations 204(1) (2004), 5–55.Google Scholar
Fonseca, I., Malý, J. and Mingione, G., Scalar minimizers with fractal singular sets, Arch. Ration. Mech. Anal. 172(2) (2004), 295–307.Google Scholar
Futamura, T. and Mizuta, Y., Maximal functions for Lebesgue spaces with variable exponent approaching 1, Hiroshima Math. J. 36(1) (2006), 23–28.Google Scholar
Guliyev, V. S., Hasanov, J. J. and Samko, S. G., Maximal, potential and singular operators in the local “complementary” variable exponent Morrey type spaces, J. Math. Anal. Appl. 401(1) (2013), 72–84.Google Scholar
Guliyev, V. S., Hasanov, S. G. and Sawano, Y., Decompositions of local Morrey-type spaces, Positivity 21(1) (2017), 1223–1252.Google Scholar
Harjulehto, P., Hästö, P. and Karppinen, A., Local higher integrability of the gradient of a quasiminimizer under generalized Orlicz growth conditions, Nonlinear Anal. 177 (2018), 543–552.Google Scholar
Hästö, P., The maximal operator in Lebesgue spaces with variable exponent near 1, Math. Nachr. 280(1–2) (2007), 74–82.Google Scholar
Hästö, P., The maximal operator on generalized Orlicz spaces, J. Funct. Anal. 269(12) (2015), 4038–4048; Corrigendum to The maximal operator on generalized Orlicz spaces, J. Funct. Anal. 271(1) (2016), 240–243.Google Scholar
Kováčik, O. and Rákosník, J., On spaces L p (x) and W k, p (x), Czechoslovak Math. J. 41 (1991), 592–618.Google Scholar
Maeda, F. Y., Mizuta, Y. and Shimomura, T., Variable exponent weighted norm inequality for generalized Riesz potentials on the unit ball, Collect. Math. 69 (2018), 377–394.Google Scholar
Mizuta, Y. and Ohno, T., Sobolev’s theorem and duality for Herz–Morrey spaces of variable exponent, Ann. Acad. Sci. Fenn. Math. 39 (2014), 389–416.Google Scholar
Mizuta, Y. and Ohno, T., Herz–Morrey spaces of variable exponent, Riesz potential operator and duality, Complex Var. Elliptic Equ. 60(2) (2015), 211–240.Google Scholar
Mizuta, Y., Ohno, T. and Shimomura, T., Integrability of maximal functions for generalized Lebesgue spaces with variable exponent, Math. Nachr. 281 (2008), 386–395.Google Scholar
Mizuta, Y., Ohno, T. and Shimomura, T., “Integrability of maximal functions for generalized Lebesgue spaces L p (⋅)(logL)q (⋅)”, in Potential Theory and Stochastics in Albac, Theta Series in Advanced Mathematics 11, Theta, Bucharest, 2009, 193–202.Google Scholar
Mizuta, Y. and Shimomura, T., Differentiability and Hölder continuity of Riesz potentials of Orlicz functions, Analysis (Munich) 20(3) (2000), 201–223.Google Scholar
Samko, S., Variable exponent Herz spaces, Mediterr. J. Math. 10(4) (2013), 2007–2025.Google Scholar
Stein, E. M., Singular Integrals and Differentiability Properties of Functions, Princeton University Press, Princeton, 1970.Google Scholar