Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-04T22:01:28.315Z Has data issue: false hasContentIssue false
  • English
  • Français

GROTHENDIECK GROUPS OF TRIANGULATED CATEGORIES VIA CLUSTER TILTING SUBCATEGORIES

Part of: Homological methods Abelian categories

Published online by Cambridge University Press:  11 June 2020

FRANCESCA FEDELE Open the ORCID record for FRANCESCA FEDELE [Opens in a new window]
FRANCESCA FEDELE*
Affiliation:
School of Mathematics, Statistics and Physics, Newcastle University, Newcastle upon TyneNE1 7RU, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 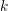$k$ be a field, and let 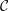${\mathcal{C}}$ be a 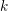$k$-linear, Hom-finite triangulated category with split idempotents. In this paper, we show that under suitable circumstances, the Grothendieck group of 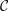${\mathcal{C}}$, denoted by 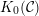$K_{0}({\mathcal{C}})$, can be expressed as a quotient of the split Grothendieck group of a higher cluster tilting subcategory of 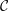${\mathcal{C}}$. The results we prove are higher versions of results on Grothendieck groups of triangulated categories by Xiao and Zhu and by Palu. Assume that 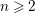$n\geqslant 2$ is an integer; 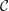${\mathcal{C}}$ has a Serre functor $\mathbb{S}$ and an $n$-cluster tilting subcategory 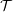${\mathcal{T}}$ such that 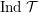$\operatorname{Ind}{\mathcal{T}}$ is locally bounded. Then, for every indecomposable 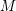$M$ in 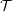${\mathcal{T}}$, there is an Auslander–Reiten 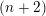$(n+2)$-angle in 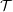${\mathcal{T}}$ of the form 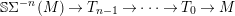$\mathbb{S}\unicode[STIX]{x1D6F4}^{-n}(M)\rightarrow T_{n-1}\rightarrow \cdots \rightarrow T_{0}\rightarrow M$ and

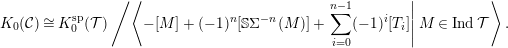$$\begin{eqnarray}K_{0}({\mathcal{C}})\cong K_{0}^{\text{sp}}({\mathcal{T}})\left/\left\langle -[M]+(-1)^{n}[\mathbb{S}\unicode[STIX]{x1D6F4}^{-n}(M)]+\left.\mathop{\sum }_{i=0}^{n-1}(-1)^{i}[T_{i}]\right|M\in \operatorname{Ind}{\mathcal{T}}\right\rangle .\right.\end{eqnarray}$$
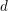Assume now that $d$ is a positive integer and 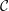${\mathcal{C}}$ has a 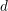$d$-cluster tilting subcategory 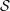${\mathcal{S}}$ closed under 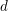$d$-suspension. Then, 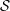${\mathcal{S}}$ is a so-called 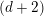$(d+2)$-angulated category whose Grothendieck group 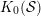$K_{0}({\mathcal{S}})$ can be defined as a certain quotient of 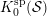$K_{0}^{\text{sp}}({\mathcal{S}})$. We will show
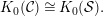$$\begin{eqnarray}K_{0}({\mathcal{C}})\cong K_{0}({\mathcal{S}}).\end{eqnarray}$$
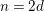 Moreover, assume that $n=2d$, that all the above assumptions hold, and that 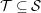${\mathcal{T}}\subseteq {\mathcal{S}}$. Then our results can be combined to express 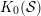$K_{0}({\mathcal{S}})$ as a quotient of 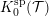$K_{0}^{\text{sp}}({\mathcal{T}})$.

MSC classification

Primary: 16E20: Grothendieck groups, $K$-theory, etc. 18E30: Derived categories, triangulated categories
Type
Article
Information
Nagoya Mathematical Journal , Volume 244 , December 2021 , pp. 204 - 231
Check for updates
Copyright
© 2020 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, M., Representation theory of Artin algebras II , Comm. Algebra 1 (1974), 269–310.CrossRefGoogle Scholar
Auslander, M., Relations for Grothendieck groups of artin algebras , Proc. Amer. Math. Soc. 91 (1984), 336–340.Google Scholar
Baur, K. and Marsh, R. J., A geometric description of m-cluster categories , Trans. Amer. Math. Soc. 360 (2008), 5789–5803.CrossRefGoogle Scholar
Bergh, P. T. and Thaule, M., The Grothendieck group of an n-angulated category , J. Pure Appl. Algebra 218 (2014), 354–366.CrossRefGoogle Scholar
Butler, M. C. R., Grothendieck Groups and Almost Split Sequences, Lecture Notes in Mathematics 822 , Springer, Berlin, Heidelberg, 1981, 357–368.Google Scholar
Gabriel, P. and Roiter, A. V., Representations of Finite-dimensional Algebras, Springer Science and Business Media 73 , 1997.CrossRefGoogle Scholar
Geiss, C., Keller, B. and Oppermann, S., n-angulated categories , J. Reine Angew. Math. 675 (2013), 101–120.Google Scholar
Iyama, O., Cluster-tilting for higher Auslander algebras , Adv. Math. 226 (2011), 1–61.Google Scholar
Iyama, O. and Oppermann, S., Stable categories of higher preprojective algebras , Adv. Math. 244 (2013), 23–68.CrossRefGoogle Scholar
Iyama, O. and Yoshino, Y., Mutation in triangulated categories and rigid Cohen–Macaulay modules , Invent. Math. 172 (2008), 117–168.Google Scholar
Jasso, G. and Külshammer, J., Higher Nakayama algebras I: construction , Adv. Math. 351 (2019), 1139–1200.CrossRefGoogle Scholar
Jørgensen, P., Tropical friezes and the index in higher homological algebra, Math. Proc. Cambridge Philos. Soc. (to appear), doi:10.1017/S0305004120000031.CrossRefGoogle Scholar
Murphy, J., Derived equivalence classification of m-cluster tilted algebras of type A n , J. Algebra 323 (2010), 920–965.CrossRefGoogle Scholar
Oppermann, S. and Thomas, H., Higher-dimensional cluster combinatorics and representation theory , J. Eur. Math. Soc. 14 (2012), 1679–1737.Google Scholar
Palu, Y., Grothendieck group and generalized mutation rule for 2-Calabi–Yau triangulated categories , J. Pure Appl. Algebra 213 (2009), 1438–1449.CrossRefGoogle Scholar
Pescod, D., Homological algebra and friezes, Ph.D. thesis, Newcastle University, 2017.Google Scholar
Thomas, H., Defining an m-cluster category , J. Algebra 318 (2007), 37–46.CrossRefGoogle Scholar
Xiao, J. and Zhu, B., Relations for the Grothendieck groups of triangulated categories , J. Algebra 257 (2002), 37–50.CrossRefGoogle Scholar
Zhou, P., Grothendieck groups and Auslander–Reiten $(d+2)$ -angles, preprint, 2019,arXiv:math.RT/1912.11397.Google Scholar