Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T06:43:30.831Z Has data issue: false hasContentIssue false
  • English
  • Français

A geometric proof of a reciprocity law

Published online by Cambridge University Press:  22 January 2016

Richard Hill
Richard Hill*
Affiliation:
Mathematisches Institut der Georg August Universität Göttingen
*
Max-Planck-Institut für Mathematik, Gottfried-Claren-Straße 26 53225 Bonn, Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove the reciprocity law for a Kummer extension of an algebraic number field K. The proof is similar to the proof of the same theorem by Kubota [14, 15]. Such methods were applied by Gauss [6, 7] to the cases K ═ Q, 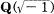and by Habicht [8] to the case 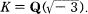. We now discuss informally the structure of the proof. All definitions and statements made at this stage are only approximations to the truth, and shouldn’t be used as references for the later chapters.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 137 , March 1995 , pp. 77 - 144
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

References

[ 1 ] Cassels, J. W. S., On Kummer Sums, Proc. London Math. Soc, (3), 21 (1970), 19–27.Google Scholar
[ 2 ] Furtwängler, Ph., Uber die Reziprozitätsgesetz zwischen l ten Potenzreste in algebraischen Zahlkörpern, wenn l eine ungerade Primzahl bedeutet, Math. Annalen, 58.Google Scholar
[ 3 ] Furtwängler, Ph., Die Reziprozitätsgesetze für Potenzreste mit Primzahlexponenten in algebraischen Zahlkörpern, I, Math. Annalen, 67 (1909), 1–31.Google Scholar
[ 4 ] Furtwängler, Ph., Die Reziprozitátsgesetze für Potenzreste mit Primzahlexponenten in algebraischen Zahlkõrpern, II, Math. Annalen, 72 (1912), 346–386.Google Scholar
[ 5 ] Furtwängler, Ph., Die Reziprozitátsgesetze für Potenzreste mit Primzahlexponenten in algebraischen Zahlkõrpern, III, Math. Annalen, 74 (1913), 413–429.CrossRefGoogle Scholar
[ 6 ] Gauß, C. F., Zur Théorie der biquadratischen Reste, Werke, Band 2, 313 – 385.Google Scholar
[ 7 ] Gauß, C. F., Disquisitiones Arithmeticae, Art. 133, Werke Band I, S. 101.Google Scholar
[ 8 ] Habicht, , Ein elementarer Beweis des kubischen Reziprozitätsgesetzes, Math. Annalen, 139 (1959–60), 343–365.Google Scholar
[ 9 ] Hilbert, D., Die Theorie der algebraischen Zahlkörper, Jahresbericht der Deutschen Mathematiker-Vereinigung, Band 4, (1894–95).Google Scholar
[10] Über die Theorie des relativquadratischen Zahlkörpers, Math. Annalen Bd. 51 (1898), 1–127.CrossRefGoogle Scholar
[11] Ito, Hiroshi, On a property of elliptic Dedekind sums, J. Number Theory, 27 (1987) 17–21.Google Scholar
[12] Ito, Hiroshi, Dedekind sums and quadratic residue symbols, Nagoya Math. J., 118 (1990) 35–43.Google Scholar
[13] Ito, Hiroshi, A note on Dedekind sums, in Number Theory, Proc. 1st Conf. Canadian Number Theory Association, Banff/Alberta (Canada) 1988, (1990), 239–248.Google Scholar
[14] Kubota, T., Geometry of Numbers and Class Field Theory, Japan. J. Math., 13, No. 2 (1987), 235–275.Google Scholar
[15] Kubota, T., Geometric Foundation of Class Field Theory, (in Japanese) Sugaka 44, 1 (1992), 1–12.Google Scholar
[16] Massey, , Singular Homology Theory, Graduate Texts in Mathematics, Springer Verlag.Google Scholar
[17] Matthews, C. R., Gauss Sums and Elliptic Functions I, The Kummer Sum, Invent. Math., 52 (1979), 163–185.CrossRefGoogle Scholar
[18] Matthews, C. R., Gauss Sums and Elliptic Functions II. The Quartic Sum, Invent. Math., 54 (1979), 23–52.Google Scholar
[19] Schering, , Verallgemeinerung des Gaußischen Criterium für den quadratischen Rest-charakter einer Zahl in Bezug auf eine andere, Werke Band I, 285–286.Google Scholar
[20] Rademacher, und Grosswald, Dedekind sums, Carus Mathematical Monographs, No 16, Mathematical Assoc. America, Washington D. C, (1972).Google Scholar
[21] Szech, , Dedekindsummen mit elliptischen Funktionen, Invent. Math., 76 (1984), 523–551.Google Scholar
[22] Szech, , Dedekind sums and power residue symbols, Compositio. Math., 59 (1986), 89–112.Google Scholar
[23] Szech, , Theta functions on the hyperbolic three space, Kokyuroku RIMS, Kyoto Univ., No. 603 (1987), 9–20.Google Scholar
[24] Weil, A., Basic Number Theory, Grundlehren der Math. Wissenschaften in Einzeldarstellung Band 144, Springer-Verlag (1967).Google Scholar