Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T23:00:09.367Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Radon Transform and Lévy’s Brownian Motion, I*)

Published online by Cambridge University Press:  22 January 2016

Akio Noda
Akio Noda*
Affiliation:
Department of Mathematics Aichi University of Education, Kariya 448, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In connection with a Gaussian system X = {X(x); x ∈ M} called Lévy’s Brownian motion (Definition 1), we shall introduce two integral transformations of special type—one is a generalized Radon transform R on a measure space (M, m), and the other is a dual Radon transform R* on another measure space (H, v) such that H ⊂ 2M, the set of all subsets of M (Definition 2). To each Lévy’s Brownian motion X, there is attached a distance d(x, y):= E[(X(x) — X(y)2] on M having a notable property named L1-embeddability. The above measure v on H is then chosen to satisfy

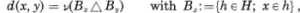
where Δ stands for the symmetric difference.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 105 , March 1987 , pp. 71 - 87
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1987

Footnotes

*)

Contribution to the research project Reconstruction, Ko 506/8-1, of the German Research Council (DFG), directed by Professor D. Kölzow, Erlangen.

References

[ 1 ] Assouad, P., Produit tensoriel, distances extrémales et realisation de covariance, I et II, C. R. Acad. Sci. Paris Ser. A, 288 (1979), 649-652 et 675–677.Google Scholar
[ 2 ] Assouad, P. et Deza, M., Espaces métriques plongeables dans un hypercube: Aspects combinatories, Ann. Discrete Math., 8 (1980), 197–210.CrossRefGoogle Scholar
[ 3 ] Assouad, P. and Deza, M., Metric subspaces of L1 , Publications math. d’Orsay, Université de Paris-Sud, 1982.Google Scholar
[ 4 ] Campi, S., On the reconstruction of a function on a sphere by its integrals over great circles, Boll. Un. Math. Ital. (5), 18-c (1981), 195–215.Google Scholar
[ 5 ] Cartier, P., Une étude des covariances measurables, Math. Analysis and Applications, Part A, Advances in Math. Supplementary Studies, 7A (1981), 267–316.Google Scholar
[ 6 ] Chentsov, N. N., Lévy Brownian motion for several parameters and generalized white noise, Theory Probab. Appl., 2 (1957), 265-266 (English translation).CrossRefGoogle Scholar
[ 7 ] Cormack, A. M. and Quinto, E. T., A Radon transform on spheres through the origin in Rn and applications to the Darboux equation, Trans. Amer. Math. Soc, 260 (1980), 575–581.Google Scholar
[ 8 ] Deans, S. R., The Radon transform and some of its applications, John Wiley & Sons, New York, 1983.Google Scholar
[ 9 ] Diaconis, P. and Graham, R. L., The Radon transform on Zk 2 , Pacific J. Math., 118 (1985), 323–345.CrossRefGoogle Scholar
[10] Erdélyi, A. Magnus, W., Oberhettinger, F. and Tricomi, F. G., Higher transcendental functions (Bateman manuscript project), Vol. II, McGraw-Hill, New York, 1953.Google Scholar
[11] Funk, P., Über Flächen mit lauter geschlossenen geodätischen Linien, Math. Ann., 74 (1913), 278–300.CrossRefGoogle Scholar
[12] Funk, P., Über eine geometrische Anwendung der Abelschen Integralgleichung, Math. Ann., 77 (1916), 129–135.CrossRefGoogle Scholar
[13] Gangolli, R., Positive definite kernels on homogeneous spaces and certain stochastic processes related to Lévy’s Brownian motion of several parameters, Ann. Inst. H. Poincaré Sect. B, 3 (1967), 121–225.Google Scholar
[14] Graham, R. L., On isometric embeddings of graphs, in Progress in graph theory (J. A. Bondy and U.S.R. Murty, ed.), Academic Press, New York, 1984, 307–322.Google Scholar
[15] Helgason, S., The Radon transform, Birkhäuser, Boston, 1980.Google Scholar
[16] Hida, T. and Hitsuda, M., Gaussian processes (in Japanese), Kinokuniya, Tokyo, 1976.Google Scholar
[17] Karhunen, K., Über lineare Methoden in der Wahrscheinlichkeitsrechnung, Ann. Acad. Sci. Fennicae Ser. A, I. Math. Phys., 37 (1947), 79 pp.Google Scholar
[18] Kelly, J. B., Hypermetric spaces, in The geometry of metric and linear spaces, Lecture Notes in Math., No. 490, Springer-Verlag, Berlin, 1975, 17–31.Google Scholar
[19] Lévy, P., Problèmes concrets d’analyse fonctionnelle, Gauthier-Villars, Paris, 1951.Google Scholar
[20] Lévy, P., Processus stochastiques et mouvement brownien, Gauthier-Villars, Paris, 1965.Google Scholar
[21] Lévy, P., Le mouvement brownien fonction d’un point de la sphère de Riemann, Rend. Circ. Mat. Palermo (2), 8 (1959), 1–14.CrossRefGoogle Scholar
[22] Lifshits, M. A., On representation of Lévy’s fields by indicators, Theory Probab. Appl., 24 (1979), 629–633 (English translation).CrossRefGoogle Scholar
[23] Ludwig, D., The Radon transform on Euclidean space, Comm. Pure Appl. Math., 19 (1966), 49–81.CrossRefGoogle Scholar
[24] McKean, H. P., Brownian motion with a several-dimensional time, Theory Probab. Appl., 8 (1963), 335–354.CrossRefGoogle Scholar
[25] Molcan, G. M., The Markov property of Levy fields on spaces of constant curvature, Soviet Math. Dokl., 16 (1975), 528–532.Google Scholar
[26] Morozova, E. A. and Chentsov, N. N., Lévy’s, P. random fields, Theory Probab. Appl., 13 (1968), 153–156 (English translation).CrossRefGoogle Scholar
[27] Noda, A., Lévy’s Brownian motion; Total positivity structure of M (t)-process and deterministic character, Nagoya Math. J., 94 (1984), 137–164.CrossRefGoogle Scholar
[28] Quinto, E. T., The dependence of the generalized Radon transform on defining measures, Trans. Amer. Math. Soc, 257 (1980), 331–346.CrossRefGoogle Scholar
[29] Quinto, E. T., Null spaces and ranges for the classical and spherical Radon transforms, J. Math. Anal. Appl., 90 (1982), 408–420.CrossRefGoogle Scholar
[30] Quinto, E. T., Singular value decompositions and inversion methods for the exterior Radon transform and a spherical transform, J. Math. Anal. Appl., 95 (1983), 437–448.CrossRefGoogle Scholar
[31] Radon, J., Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten, Ber. Verh. Sachs. Akad. Wiss. Leipzig, Math.-Nat. kl., 69 (1917), 262–277.Google Scholar
[32] Schneider, R., Über eine Integralgleichung in der Theorie der konvexen Körper, Math. Nachr., 44 (1970), 55–75.CrossRefGoogle Scholar
[33] Seeley, R. T., Spherical harmonics, Amer. Math. Monthly, 73 (1966), 115–121.CrossRefGoogle Scholar
[34] Strichartz, R. S., Radon inversion—variations on a theme, Amer. Math. Monthly, 89 (1982), 377-384 and 420–423.CrossRefGoogle Scholar
[35] Takenaka, S. Kubo, I. and Urakawa, H., Brownian motion parametrized with metric spaces of constant curvature, Nagoya Math. J., 82 (1981), 131–140.CrossRefGoogle Scholar