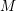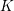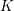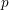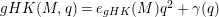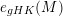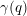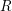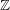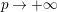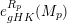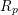Introduction
Let
![]() $R$
be a
$R$
be a
![]() $d$
-dimensional standard graded
$d$
-dimensional standard graded
![]() $K$
-domain over a perfect field
$K$
-domain over a perfect field
![]() $K$
of characteristic
$K$
of characteristic
![]() $p>0$
that is
$p>0$
that is
![]() $F$
-finite. For every finitely generated
$F$
-finite. For every finitely generated
![]() $R$
-module
$R$
-module
![]() $M$
and every natural number
$M$
and every natural number
![]() $e$
, we denote by
$e$
, we denote by
![]() $F^{e\ast }(M)=M\otimes _{R}\text{}^{e}R$
the
$F^{e\ast }(M)=M\otimes _{R}\text{}^{e}R$
the
![]() $e\text{th}$
iteration of the Frobenius functor given by base change along the Frobenius homomorphism. In particular, if
$e\text{th}$
iteration of the Frobenius functor given by base change along the Frobenius homomorphism. In particular, if
![]() $I$
is an ideal of
$I$
is an ideal of
![]() $R$
, we have that
$R$
, we have that
![]() $F^{e\ast }(R/I)\cong R/I^{[p^{e}]}$
. We denote by
$F^{e\ast }(R/I)\cong R/I^{[p^{e}]}$
. We denote by
![]() $q=p^{e}$
a power of the characteristic. Let
$q=p^{e}$
a power of the characteristic. Let
![]() $M$
be a graded
$M$
be a graded
![]() $R$
-module. The function
$R$
-module. The function
and the limit
are called the generalized Hilbert–Kunz function and the generalized Hilbert–Kunz multiplicity of
![]() $M$
, respectively. If
$M$
, respectively. If
![]() $I$
is an
$I$
is an
![]() $R_{+}$
-primary ideal, then
$R_{+}$
-primary ideal, then
![]() $gHK(R/I,q)$
and
$gHK(R/I,q)$
and
![]() $e_{gHK}(R/I)$
coincide with the classical Hilbert–Kunz function and multiplicity. For a survey on the classical Hilbert–Kunz function and multiplicity, see [Reference Huneke10].
$e_{gHK}(R/I)$
coincide with the classical Hilbert–Kunz function and multiplicity. For a survey on the classical Hilbert–Kunz function and multiplicity, see [Reference Huneke10].
The generalized Hilbert–Kunz function and multiplicity were first introduced, under a different name and notation, by Epstein and Yao in [Reference Epstein and Yao8], and studied in detail by Dao and Smirnov in [Reference Dao and Smirnov6], where they proved the existence of
![]() $e_{gHK}(M)$
under some assumptions, for example if
$e_{gHK}(M)$
under some assumptions, for example if
![]() $M$
is a module over a Cohen–Macaulay isolated singularity. In the same paper, they studied the behavior of the function
$M$
is a module over a Cohen–Macaulay isolated singularity. In the same paper, they studied the behavior of the function
![]() $gHK(M,q)$
and compared it with the classical Hilbert–Kunz function. Further study of the generalized Hilbert–Kunz function and multiplicity has been made by Dao and Watanabe in [Reference Dao and Watanabe7], where they computed
$gHK(M,q)$
and compared it with the classical Hilbert–Kunz function. Further study of the generalized Hilbert–Kunz function and multiplicity has been made by Dao and Watanabe in [Reference Dao and Watanabe7], where they computed
![]() $e_{gHK}(M)$
if
$e_{gHK}(M)$
if
![]() $M$
is a module over a ring of finite Cohen–Macaulay type, or it is an ideal of a normal toric singularity.
$M$
is a module over a ring of finite Cohen–Macaulay type, or it is an ideal of a normal toric singularity.
In this paper, we study the function
![]() $gHK(M,q)$
for a graded module
$gHK(M,q)$
for a graded module
![]() $M$
over a two-dimensional standard graded normal domain over an algebraically closed field. In [Reference Brenner3], Brenner proved that if
$M$
over a two-dimensional standard graded normal domain over an algebraically closed field. In [Reference Brenner3], Brenner proved that if
![]() $I$
is a homogeneous
$I$
is a homogeneous
![]() $R_{+}$
-primary ideal, then the Hilbert–Kunz function of
$R_{+}$
-primary ideal, then the Hilbert–Kunz function of
![]() $I$
has the following form:
$I$
has the following form:
where
![]() $e_{HK}(I)$
is a rational number and
$e_{HK}(I)$
is a rational number and
![]() $\unicode[STIX]{x1D6FE}(q)$
is a bounded function, which is eventually periodic if
$\unicode[STIX]{x1D6FE}(q)$
is a bounded function, which is eventually periodic if
![]() $K$
is the algebraic closure of a finite field. In [Reference Dao and Smirnov6, Example 6.2], Dao and Smirnov exhibited numerical evidence that in this setting also the generalized Hilbert–Kunz function has the same form. Using an extension of the methods of Brenner, we are able to prove their claim. In fact, we obtain in Theorem 3.2 that the generalized Hilbert–Kunz function of a graded module
$K$
is the algebraic closure of a finite field. In [Reference Dao and Smirnov6, Example 6.2], Dao and Smirnov exhibited numerical evidence that in this setting also the generalized Hilbert–Kunz function has the same form. Using an extension of the methods of Brenner, we are able to prove their claim. In fact, we obtain in Theorem 3.2 that the generalized Hilbert–Kunz function of a graded module
![]() $M$
has the form
$M$
has the form
where
![]() $\unicode[STIX]{x1D6FE}(q)$
is a bounded function, which is eventually periodic if
$\unicode[STIX]{x1D6FE}(q)$
is a bounded function, which is eventually periodic if
![]() $K$
is the algebraic closure of a finite field. Moreover, we give an explicit formula for
$K$
is the algebraic closure of a finite field. Moreover, we give an explicit formula for
![]() $e_{gHK}(M)$
in terms of the Hilbert–Kunz slope of certain locally free sheaves on the projective curve
$e_{gHK}(M)$
in terms of the Hilbert–Kunz slope of certain locally free sheaves on the projective curve
![]() $Y=\text{Proj}R$
. As a consequence of this fact, we obtain that the generalized Hilbert–Kunz multiplicity
$Y=\text{Proj}R$
. As a consequence of this fact, we obtain that the generalized Hilbert–Kunz multiplicity
![]() $e_{gHK}(M)$
exists, and it is a rational number.
$e_{gHK}(M)$
exists, and it is a rational number.
Furthermore, in the last section of the paper, we consider the following problem. Assume that
![]() $R$
is a standard graded
$R$
is a standard graded
![]() $\mathbb{Z}$
-domain of relative dimension 2, and
$\mathbb{Z}$
-domain of relative dimension 2, and
![]() $M$
is a graded
$M$
is a graded
![]() $R$
-module. For each prime number
$R$
-module. For each prime number
![]() $p$
, we may consider the reduction
$p$
, we may consider the reduction
![]() $R_{p}$
of
$R_{p}$
of
![]() $R$
mod
$R$
mod
![]() $p$
and the extended module
$p$
and the extended module
![]() $M_{p}:=M\otimes _{R}R_{p}$
. For this module, we compute the generalized Hilbert–Kunz multiplicity
$M_{p}:=M\otimes _{R}R_{p}$
. For this module, we compute the generalized Hilbert–Kunz multiplicity
![]() $e_{gHK}^{R_{p}}(M_{p})$
, and we ask whether the limit
$e_{gHK}^{R_{p}}(M_{p})$
, and we ask whether the limit
exists. Using a result of Trivedi [Reference Trivedi12], we are able to prove (Theorem 4.4) that the previous limit exists, and it is in fact a rational number, assuming that the rings
![]() $R_{p}$
are normal two-dimensional domains for almost all prime numbers.
$R_{p}$
are normal two-dimensional domains for almost all prime numbers.
After submitting the first version of this paper, the referee and Asgharzadeh pointed us to a recent paper of Vraciu [Reference Vraciu13]. There, she provides another method to prove Theorem 3.2 for ideals by showing that under suitable conditions, which are fulfilled in our situation, the generalized Hilbert–Kunz function of a homogeneous ideal can be expressed as a
![]() $\mathbb{Z}$
-linear combination of the classical Hilbert–Kunz function of
$\mathbb{Z}$
-linear combination of the classical Hilbert–Kunz function of
![]() $R_{+}$
-primary ideals. The relevant condition is called the
$R_{+}$
-primary ideals. The relevant condition is called the
![]() $(LC)$
property, and was introduced by Hochster and Huneke in [Reference Hochster and Huneke9]. This condition is known to hold in some special cases, but it is an open problem whether it holds in a more general setting (see [Reference Asgharzadeh1]).
$(LC)$
property, and was introduced by Hochster and Huneke in [Reference Hochster and Huneke9]. This condition is known to hold in some special cases, but it is an open problem whether it holds in a more general setting (see [Reference Asgharzadeh1]).
1 Reflexive modules
We recall some preliminary facts concerning reflexive modules. Let
![]() $R$
be a two-dimensional normal domain with homogeneous maximal ideal
$R$
be a two-dimensional normal domain with homogeneous maximal ideal
![]() $\mathfrak{m}$
, and let
$\mathfrak{m}$
, and let
![]() $U$
be the punctured spectrum of
$U$
be the punctured spectrum of
![]() $R$
; that is,
$R$
; that is,
![]() $U=\text{Spec}R\setminus \{\mathfrak{m}\}$
.
$U=\text{Spec}R\setminus \{\mathfrak{m}\}$
.
We denote by
![]() $(-)^{\ast }$
the functor
$(-)^{\ast }$
the functor
![]() $\text{Hom}_{R}(-,R)$
. If
$\text{Hom}_{R}(-,R)$
. If
![]() $M$
is an
$M$
is an
![]() $R$
-module, then the module
$R$
-module, then the module
![]() $M^{\ast \ast }$
is called the reflexive hull of
$M^{\ast \ast }$
is called the reflexive hull of
![]() $M$
. There is a canonical map
$M$
. There is a canonical map
If
![]() $\unicode[STIX]{x1D706}$
is injective,
$\unicode[STIX]{x1D706}$
is injective,
![]() $M$
is said to be torsionless; if
$M$
is said to be torsionless; if
![]() $\unicode[STIX]{x1D706}$
is an isomorphism, then
$\unicode[STIX]{x1D706}$
is an isomorphism, then
![]() $M$
is called reflexive. Finitely generated projective modules are reflexive, but the converse does not hold in general. We recall the following geometric characterization of the reflexive hull in the normal situation (cf. [Reference Burban and Drozd5, Proposition 3.10]):
$M$
is called reflexive. Finitely generated projective modules are reflexive, but the converse does not hold in general. We recall the following geometric characterization of the reflexive hull in the normal situation (cf. [Reference Burban and Drozd5, Proposition 3.10]):
where
![]() $\widetilde{M}$
denotes the coherent sheaf associated to the module
$\widetilde{M}$
denotes the coherent sheaf associated to the module
![]() $M$
. It follows that the restriction of this sheaf to the punctured spectrum
$M$
. It follows that the restriction of this sheaf to the punctured spectrum
![]() $\widetilde{M}|_{U}$
coincides with the sheaf
$\widetilde{M}|_{U}$
coincides with the sheaf
![]() $\widetilde{M^{\ast \ast }}|_{U}$
on
$\widetilde{M^{\ast \ast }}|_{U}$
on
![]() $U$
. Moreover, if
$U$
. Moreover, if
![]() $M$
is reflexive, the sheaf
$M$
is reflexive, the sheaf
![]() $\widetilde{M}|_{U}$
is locally free.
$\widetilde{M}|_{U}$
is locally free.
The following lemma is a well-known fact (see [Reference Bruns and Herzog4, Proposition 1.4.1]). We give a proof here for the sake of completeness.
Lemma 1.1. Let
![]() $R$
be a normal domain of dimension at least
$R$
be a normal domain of dimension at least
![]() $2$
with homogeneous maximal ideal
$2$
with homogeneous maximal ideal
![]() $\mathfrak{m}$
, and let
$\mathfrak{m}$
, and let
![]() $I$
be a reflexive submodule of
$I$
be a reflexive submodule of
![]() $R^{n}$
. Then,
$R^{n}$
. Then,
Proof. We consider the short exact sequence
![]() $0\rightarrow I\rightarrow R^{n}\rightarrow R^{n}/I\rightarrow 0$
, and we apply the local cohomology functor
$0\rightarrow I\rightarrow R^{n}\rightarrow R^{n}/I\rightarrow 0$
, and we apply the local cohomology functor
![]() $H_{\mathfrak{m}}^{0}(-)$
. We obtain a long exact sequence
$H_{\mathfrak{m}}^{0}(-)$
. We obtain a long exact sequence
Since
![]() $R^{n}$
and
$R^{n}$
and
![]() $I$
are reflexive modules over a normal domain, they have depth at least
$I$
are reflexive modules over a normal domain, they have depth at least
![]() $2$
. It follows that
$2$
. It follows that
![]() $H_{\mathfrak{m}}^{0}(R^{n})=H_{\mathfrak{m}}^{1}(I)=0$
, hence
$H_{\mathfrak{m}}^{0}(R^{n})=H_{\mathfrak{m}}^{1}(I)=0$
, hence
![]() $H_{\mathfrak{m}}^{0}(R^{n}/I)=0$
too. ◻
$H_{\mathfrak{m}}^{0}(R^{n}/I)=0$
too. ◻
We mention also the following result (cf. [Reference Dao and Watanabe7, Proposition 2.2]), concerning the generalized Hilbert–Kunz multiplicity of reflexive ideals.
Proposition 1.2. Let
![]() $R$
be a standard graded domain of dimension
$R$
be a standard graded domain of dimension
![]() $2$
, and let
$2$
, and let
![]() $I$
be a homogeneous reflexive ideal of
$I$
be a homogeneous reflexive ideal of
![]() $R$
. Then,
$R$
. Then,
![]() $e_{gHK}(R/I)=0$
if and only if
$e_{gHK}(R/I)=0$
if and only if
![]() $I$
is principal.
$I$
is principal.
The fact that principal reflexive ideals have generalized Hilbert–Kunz multiplicity
![]() $0$
holds also in dimension
$0$
holds also in dimension
![]() ${\geqslant}2$
, and is a consequence of Lemma 1.1. In fact, if
${\geqslant}2$
, and is a consequence of Lemma 1.1. In fact, if
![]() $I$
is a principal ideal, then
$I$
is a principal ideal, then
![]() $I^{[p^{e}]}$
is again principal, and in particular reflexive. It follows that
$I^{[p^{e}]}$
is again principal, and in particular reflexive. It follows that
![]() $H_{R_{+}}^{0}(F^{e\ast }(R/I))\cong H_{R_{+}}^{0}(R/I^{[p^{e}]})=0$
, so
$H_{R_{+}}^{0}(F^{e\ast }(R/I))\cong H_{R_{+}}^{0}(R/I^{[p^{e}]})=0$
, so
![]() $e_{gHK}(R/I)=0$
.
$e_{gHK}(R/I)=0$
.
Lemma 1.3. Let
![]() $R$
be a normal
$R$
be a normal
![]() $K$
-domain of dimension
$K$
-domain of dimension
![]() $d\geqslant 2$
over an algebraically closed field
$d\geqslant 2$
over an algebraically closed field
![]() $K$
of prime characteristic
$K$
of prime characteristic
![]() $p$
. Let
$p$
. Let
![]() $I$
be a nonzero homogeneous ideal of
$I$
be a nonzero homogeneous ideal of
![]() $R$
such that
$R$
such that
![]() $e_{gHK}(R/I)$
exists, and let
$e_{gHK}(R/I)$
exists, and let
![]() $f\neq 0$
be a homogeneous element of
$f\neq 0$
be a homogeneous element of
![]() $R$
. Then,
$R$
. Then,
Proof. From the short exact sequence
![]() $0\rightarrow I\rightarrow R\rightarrow R/I\rightarrow 0$
and the corresponding long exact sequence of local cohomology modules with support in
$0\rightarrow I\rightarrow R\rightarrow R/I\rightarrow 0$
and the corresponding long exact sequence of local cohomology modules with support in
![]() $\mathfrak{m}:=R_{+}$
, we obtain that
$\mathfrak{m}:=R_{+}$
, we obtain that
![]() $H_{\mathfrak{m}}^{0}(R/I)\cong H_{\mathfrak{m}}^{1}(I)$
. It follows that the generalized Hilbert–Kunz multiplicity can be seen as
$H_{\mathfrak{m}}^{0}(R/I)\cong H_{\mathfrak{m}}^{1}(I)$
. It follows that the generalized Hilbert–Kunz multiplicity can be seen as
Then, the
![]() $R$
-module isomorphism
$R$
-module isomorphism
![]() $f^{q}I^{[q]}\cong I^{[q]}$
implies the claim.◻
$f^{q}I^{[q]}\cong I^{[q]}$
implies the claim.◻
Remark 1.4. Let
![]() $[I]$
be an element of the divisor class group
$[I]$
be an element of the divisor class group
![]() $\text{Cl}(R)$
of
$\text{Cl}(R)$
of
![]() $R$
, and let
$R$
, and let
![]() $I$
be a homogeneous reflexive ideal representative of this element. If
$I$
be a homogeneous reflexive ideal representative of this element. If
![]() $R$
is a standard graded normal
$R$
is a standard graded normal
![]() $K$
-domain of dimension
$K$
-domain of dimension
![]() $2$
, with
$2$
, with
![]() $K$
algebraically closed and of positive characteristic, we obtain a function
$K$
algebraically closed and of positive characteristic, we obtain a function
![]() $e_{gHK}(-):\text{Cl}(R)\rightarrow \mathbb{Q}$
,
$e_{gHK}(-):\text{Cl}(R)\rightarrow \mathbb{Q}$
,
![]() $[I]\mapsto e_{gHK}(R/I)$
. Thanks to Theorem 3.2 and Lemma 1.3, this function is well defined, and we have
$[I]\mapsto e_{gHK}(R/I)$
. Thanks to Theorem 3.2 and Lemma 1.3, this function is well defined, and we have
![]() $e_{gHK}([R])=0$
. This does not mean that the generalized Hilbert–Kunz multiplicity for all ideals
$e_{gHK}([R])=0$
. This does not mean that the generalized Hilbert–Kunz multiplicity for all ideals
![]() $I$
that are invertible on the punctured spectrum depends only on
$I$
that are invertible on the punctured spectrum depends only on
![]() $[I]$
. For example, the homogeneous maximal ideal
$[I]$
. For example, the homogeneous maximal ideal
![]() $\mathfrak{m}$
and its reflexive hull
$\mathfrak{m}$
and its reflexive hull
![]() $\mathfrak{m}^{\ast \ast }=R$
define the same element in the class group, but
$\mathfrak{m}^{\ast \ast }=R$
define the same element in the class group, but
![]() $e_{gHK}(R/\mathfrak{m})=e_{HK}(\mathfrak{m})\neq 0$
in general, while
$e_{gHK}(R/\mathfrak{m})=e_{HK}(\mathfrak{m})\neq 0$
in general, while
![]() $e_{gHK}(R/R)=0$
. Moreover, Proposition 1.2 implies that the preimage of
$e_{gHK}(R/R)=0$
. Moreover, Proposition 1.2 implies that the preimage of
![]() $0$
is trivial. This does not mean that the function
$0$
is trivial. This does not mean that the function
![]() $e_{gHK}(-)$
is injective, since in general it is not a group homomorphism as in the case of Example 3.6.
$e_{gHK}(-)$
is injective, since in general it is not a group homomorphism as in the case of Example 3.6.
Therefore, the following question makes sense.
Question 1.5. Given two homogeneous reflexive ideals
![]() $I$
and
$I$
and
![]() $J$
, is there a formula for
$J$
, is there a formula for
![]() $e_{gHK}([IJ])$
in terms of
$e_{gHK}([IJ])$
in terms of
![]() $e_{gHK}([I])$
and
$e_{gHK}([I])$
and
![]() $e_{gHK}([J])$
?
$e_{gHK}([J])$
?
2 The Hilbert–Kunz slope
Let
![]() $Y$
be a smooth projective curve over an algebraically closed field with a very ample invertible sheaf of degree
$Y$
be a smooth projective curve over an algebraically closed field with a very ample invertible sheaf of degree
![]() $\deg {\mathcal{O}}_{Y}(1)=\deg Y$
. We recall some classical notions of vector bundles, and some definitions from [Reference Brenner2] and [Reference Brenner3]. We refer to these papers for further details and explanations.
$\deg {\mathcal{O}}_{Y}(1)=\deg Y$
. We recall some classical notions of vector bundles, and some definitions from [Reference Brenner2] and [Reference Brenner3]. We refer to these papers for further details and explanations.
Let
![]() ${\mathcal{S}}$
be a locally free sheaf of rank
${\mathcal{S}}$
be a locally free sheaf of rank
![]() $r$
over
$r$
over
![]() $X$
. The degree of
$X$
. The degree of
![]() ${\mathcal{S}}$
is defined as the degree of the corresponding determinant line bundle
${\mathcal{S}}$
is defined as the degree of the corresponding determinant line bundle
![]() $\text{deg}{\mathcal{S}}=\deg \bigwedge ^{r}{\mathcal{S}}$
. The slope of
$\text{deg}{\mathcal{S}}=\deg \bigwedge ^{r}{\mathcal{S}}$
. The slope of
![]() ${\mathcal{S}}$
is
${\mathcal{S}}$
is
![]() $\unicode[STIX]{x1D707}({\mathcal{S}})=\deg {\mathcal{S}}/r$
. The degree is additive on short exact sequences, and moreover
$\unicode[STIX]{x1D707}({\mathcal{S}})=\deg {\mathcal{S}}/r$
. The degree is additive on short exact sequences, and moreover
![]() $\unicode[STIX]{x1D707}({\mathcal{S}}\otimes {\mathcal{T}})=\unicode[STIX]{x1D707}({\mathcal{S}})+\unicode[STIX]{x1D707}({\mathcal{T}})$
.
$\unicode[STIX]{x1D707}({\mathcal{S}}\otimes {\mathcal{T}})=\unicode[STIX]{x1D707}({\mathcal{S}})+\unicode[STIX]{x1D707}({\mathcal{T}})$
.
The sheaf
![]() ${\mathcal{S}}$
is called semistable if for every locally free subsheaf
${\mathcal{S}}$
is called semistable if for every locally free subsheaf
![]() ${\mathcal{T}}\subseteq {\mathcal{S}}$
, the inequality
${\mathcal{T}}\subseteq {\mathcal{S}}$
, the inequality
![]() $\unicode[STIX]{x1D707}({\mathcal{T}})\leqslant \unicode[STIX]{x1D707}({\mathcal{S}})$
holds. If the strict inequality
$\unicode[STIX]{x1D707}({\mathcal{T}})\leqslant \unicode[STIX]{x1D707}({\mathcal{S}})$
holds. If the strict inequality
![]() $\unicode[STIX]{x1D707}({\mathcal{T}})<\unicode[STIX]{x1D707}({\mathcal{S}})$
holds for every proper subsheaf
$\unicode[STIX]{x1D707}({\mathcal{T}})<\unicode[STIX]{x1D707}({\mathcal{S}})$
holds for every proper subsheaf
![]() ${\mathcal{T}}\subset {\mathcal{S}}$
, then
${\mathcal{T}}\subset {\mathcal{S}}$
, then
![]() ${\mathcal{S}}$
is called stable.
${\mathcal{S}}$
is called stable.
For any locally free sheaf
![]() ${\mathcal{S}}$
on
${\mathcal{S}}$
on
![]() $Y$
, there exists a unique filtration, called Harder–Narasimhan filtration,
$Y$
, there exists a unique filtration, called Harder–Narasimhan filtration,
![]() ${\mathcal{S}}_{1}\subseteq \cdots \subseteq {\mathcal{S}}_{t}={\mathcal{S}}$
, with the following properties:
${\mathcal{S}}_{1}\subseteq \cdots \subseteq {\mathcal{S}}_{t}={\mathcal{S}}$
, with the following properties:
∙
 ${\mathcal{S}}_{k}$
is locally free;
${\mathcal{S}}_{k}$
is locally free;∙
 ${\mathcal{S}}_{k}/{\mathcal{S}}_{k-1}$
is semistable;
${\mathcal{S}}_{k}/{\mathcal{S}}_{k-1}$
is semistable;∙
 $\unicode[STIX]{x1D707}({\mathcal{S}}_{k}/{\mathcal{S}}_{k-1})>\unicode[STIX]{x1D707}({\mathcal{S}}_{k+1}/{\mathcal{S}}_{k})$
.
$\unicode[STIX]{x1D707}({\mathcal{S}}_{k}/{\mathcal{S}}_{k-1})>\unicode[STIX]{x1D707}({\mathcal{S}}_{k+1}/{\mathcal{S}}_{k})$
.
If the base field has positive characteristic, we can consider the absolute Frobenius morphism
![]() $F:Y\rightarrow Y$
on the curve and its iterates
$F:Y\rightarrow Y$
on the curve and its iterates
![]() $F^{e}$
. In general, the pullback via
$F^{e}$
. In general, the pullback via
![]() $F^{e}$
of the Harder–Narasimhan filtration of
$F^{e}$
of the Harder–Narasimhan filtration of
![]() ${\mathcal{S}}$
is not the Harder–Narasimhan filtration of
${\mathcal{S}}$
is not the Harder–Narasimhan filtration of
![]() $F^{e\ast }{\mathcal{S}}$
, since the quotients
$F^{e\ast }{\mathcal{S}}$
, since the quotients
![]() $F^{e\ast }({\mathcal{S}}_{k})/F^{e\ast }({\mathcal{S}}_{k-1})$
need not be semistable.
$F^{e\ast }({\mathcal{S}}_{k})/F^{e\ast }({\mathcal{S}}_{k-1})$
need not be semistable.
In [Reference Langer11], Langer proved that for
![]() $q\gg 0$
, there exists the so-called strong Harder–Narasimhan filtration of
$q\gg 0$
, there exists the so-called strong Harder–Narasimhan filtration of
![]() $F^{e\ast }({\mathcal{S}})$
. In fact, there exists a natural number
$F^{e\ast }({\mathcal{S}})$
. In fact, there exists a natural number
![]() $e_{0}$
such that the Harder–Narasimhan filtration of
$e_{0}$
such that the Harder–Narasimhan filtration of
![]() $F^{e_{0}\ast }({\mathcal{S}})$
,
$F^{e_{0}\ast }({\mathcal{S}})$
,
has the property that the quotients
![]() $F^{e\ast }({\mathcal{S}}_{e_{0},k})/F^{e\ast }({\mathcal{S}}_{e_{0},k-1})$
of the pullback along
$F^{e\ast }({\mathcal{S}}_{e_{0},k})/F^{e\ast }({\mathcal{S}}_{e_{0},k-1})$
of the pullback along
![]() $F^{e}$
are semistable. Thus, for
$F^{e}$
are semistable. Thus, for
![]() $e\geqslant e_{0}$
, we have
$e\geqslant e_{0}$
, we have
![]() $F^{e\ast }({\mathcal{S}})=F^{(e-e_{0})\ast }(F^{e_{0}\ast }({\mathcal{S}}))$
, and the Harder–Narasimhan filtration of
$F^{e\ast }({\mathcal{S}})=F^{(e-e_{0})\ast }(F^{e_{0}\ast }({\mathcal{S}}))$
, and the Harder–Narasimhan filtration of
![]() $F^{e\ast }({\mathcal{S}})$
is given by
$F^{e\ast }({\mathcal{S}})$
is given by
For ease of notation, we put
![]() ${\mathcal{S}}_{e,k}:=F^{(e-e_{0})\ast }({\mathcal{S}}_{e_{0},k})$
for every
${\mathcal{S}}_{e,k}:=F^{(e-e_{0})\ast }({\mathcal{S}}_{e_{0},k})$
for every
![]() $e\geqslant e_{0}$
and
$e\geqslant e_{0}$
and
![]() $0\leqslant k\leqslant t$
. The length
$0\leqslant k\leqslant t$
. The length
![]() $t$
of such a sequence and the ranks of the quotients
$t$
of such a sequence and the ranks of the quotients
![]() ${\mathcal{S}}_{e,k}/{\mathcal{S}}_{e,k-1}$
are independent of
${\mathcal{S}}_{e,k}/{\mathcal{S}}_{e,k-1}$
are independent of
![]() $e$
, while the degrees are not. We define the following rational numbers:
$e$
, while the degrees are not. We define the following rational numbers:
∙
 $\bar{\unicode[STIX]{x1D707}}_{k}=\bar{\unicode[STIX]{x1D707}}_{k}({\mathcal{S}})=\frac{\unicode[STIX]{x1D707}({\mathcal{S}}_{e,k}/{\mathcal{S}}_{e,k-1})}{p^{e}}$
, where
$\bar{\unicode[STIX]{x1D707}}_{k}=\bar{\unicode[STIX]{x1D707}}_{k}({\mathcal{S}})=\frac{\unicode[STIX]{x1D707}({\mathcal{S}}_{e,k}/{\mathcal{S}}_{e,k-1})}{p^{e}}$
, where
 $\unicode[STIX]{x1D707}(-)$
denotes the usual slope of the bundle;
$\unicode[STIX]{x1D707}(-)$
denotes the usual slope of the bundle;∙
 $r_{k}=\text{rank}({\mathcal{S}}_{e,k}/{\mathcal{S}}_{e,k-1})$
;
$r_{k}=\text{rank}({\mathcal{S}}_{e,k}/{\mathcal{S}}_{e,k-1})$
;∙
 $\unicode[STIX]{x1D708}_{k}=-\frac{\bar{\unicode[STIX]{x1D707}}_{k}}{\text{deg}Y}$
.
$\unicode[STIX]{x1D708}_{k}=-\frac{\bar{\unicode[STIX]{x1D707}}_{k}}{\text{deg}Y}$
.
Remark 2.1. We point out that the numbers
![]() $\bar{\unicode[STIX]{x1D707}}$
,
$\bar{\unicode[STIX]{x1D707}}$
,
![]() $r_{k}$
and
$r_{k}$
and
![]() $\unicode[STIX]{x1D708}_{k}$
are rational and independent from
$\unicode[STIX]{x1D708}_{k}$
are rational and independent from
![]() $e$
for
$e$
for
![]() $e\gg 0$
. In fact, we have that
$e\gg 0$
. In fact, we have that
![]() $\sum _{k=1}^{t}r_{k}\unicode[STIX]{x1D707}({\mathcal{S}}_{e,k}/{\mathcal{S}}_{e,k-1})=\deg (F^{e\ast }{\mathcal{S}})=p^{e}\deg {\mathcal{S}}$
, which implies the relation
$\sum _{k=1}^{t}r_{k}\unicode[STIX]{x1D707}({\mathcal{S}}_{e,k}/{\mathcal{S}}_{e,k-1})=\deg (F^{e\ast }{\mathcal{S}})=p^{e}\deg {\mathcal{S}}$
, which implies the relation
Definition 2.2. Let
![]() ${\mathcal{S}}$
be a locally free sheaf over a projective curve over an algebraically closed field of prime characteristic, and let
${\mathcal{S}}$
be a locally free sheaf over a projective curve over an algebraically closed field of prime characteristic, and let
![]() $\bar{\unicode[STIX]{x1D707}}$
and
$\bar{\unicode[STIX]{x1D707}}$
and
![]() $r_{k}$
be as above. The Hilbert–Kunz slope of
$r_{k}$
be as above. The Hilbert–Kunz slope of
![]() ${\mathcal{S}}$
is the rational number
${\mathcal{S}}$
is the rational number
This notion was introduced by the first author in [Reference Brenner3], where he also proved Theorem 2.5 below.
Example 2.3. Let
![]() ${\mathcal{L}}$
be a line bundle, then
${\mathcal{L}}$
be a line bundle, then
![]() ${\mathcal{L}}$
is semistable of slope
${\mathcal{L}}$
is semistable of slope
![]() $\unicode[STIX]{x1D707}({\mathcal{L}})=\deg {\mathcal{L}}$
. The pullback along Frobenius is again a line bundle,
$\unicode[STIX]{x1D707}({\mathcal{L}})=\deg {\mathcal{L}}$
. The pullback along Frobenius is again a line bundle,
![]() $F^{e\ast }{\mathcal{L}}={\mathcal{L}}^{q}={\mathcal{L}}^{\otimes q}$
, with
$F^{e\ast }{\mathcal{L}}={\mathcal{L}}^{q}={\mathcal{L}}^{\otimes q}$
, with
![]() $q=p^{e}$
. It follows that
$q=p^{e}$
. It follows that
![]() $0\subseteq {\mathcal{L}}$
is the strong Harder–Narasimhan filtration of
$0\subseteq {\mathcal{L}}$
is the strong Harder–Narasimhan filtration of
![]() ${\mathcal{L}}$
, and the Hilbert–Kunz slope is just
${\mathcal{L}}$
, and the Hilbert–Kunz slope is just
Example 2.4. Let
![]() $d_{1}<d_{2}<\cdots <d_{m}$
be nonnegative integers, and let
$d_{1}<d_{2}<\cdots <d_{m}$
be nonnegative integers, and let
![]() ${\mathcal{T}}:=\bigoplus _{i=1}^{m}{\mathcal{O}}(-d_{i})^{\oplus r_{i}}$
, where
${\mathcal{T}}:=\bigoplus _{i=1}^{m}{\mathcal{O}}(-d_{i})^{\oplus r_{i}}$
, where
![]() ${\mathcal{O}}:={\mathcal{O}}_{Y}$
and
${\mathcal{O}}:={\mathcal{O}}_{Y}$
and
![]() $r_{i}\in \mathbb{N}$
. The Harder–Narasimhan filtration of
$r_{i}\in \mathbb{N}$
. The Harder–Narasimhan filtration of
![]() ${\mathcal{T}}$
is
${\mathcal{T}}$
is
The quotients are direct sums of line bundles of the same degree, so their pullbacks under Frobenius are semistable. Hence, this is also the strong Harder–Narasimhan filtration of
![]() ${\mathcal{T}}$
with invariants
${\mathcal{T}}$
with invariants
![]() $r_{k}$
, and
$r_{k}$
, and
![]() $\bar{\unicode[STIX]{x1D707}}_{k}=\deg {\mathcal{O}}(-d_{k})=-d_{k}\deg {\mathcal{O}}_{Y}(1)=-d_{k}\deg Y$
. Then, the Hilbert–Kunz slope of
$\bar{\unicode[STIX]{x1D707}}_{k}=\deg {\mathcal{O}}(-d_{k})=-d_{k}\deg {\mathcal{O}}_{Y}(1)=-d_{k}\deg Y$
. Then, the Hilbert–Kunz slope of
![]() ${\mathcal{T}}$
is
${\mathcal{T}}$
is
Theorem 2.5. (Brenner [Reference Brenner3])
Let
![]() $Y$
denote a smooth projective curve of genus
$Y$
denote a smooth projective curve of genus
![]() $g$
over an algebraically closed field of positive characteristic
$g$
over an algebraically closed field of positive characteristic
![]() $p$
, and let
$p$
, and let
![]() $q=p^{e}$
for a nonnegative integer
$q=p^{e}$
for a nonnegative integer
![]() $e$
. Let
$e$
. Let
![]() $0\rightarrow {\mathcal{S}}\rightarrow {\mathcal{T}}\rightarrow {\mathcal{Q}}\rightarrow 0$
denote a short exact sequence of locally free sheaves on
$0\rightarrow {\mathcal{S}}\rightarrow {\mathcal{T}}\rightarrow {\mathcal{Q}}\rightarrow 0$
denote a short exact sequence of locally free sheaves on
![]() $Y$
. Then, the following hold.
$Y$
. Then, the following hold.
(1) For every nonnegative integer
 $e$
, the alternating sum of the dimensions of the global sections is
$e$
, the alternating sum of the dimensions of the global sections is  $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{m\in \mathbb{Z}}\left(h^{0}(F^{e\ast }{\mathcal{S}}(m))-h^{0}(F^{e\ast }{\mathcal{T}}(m))+h^{0}(F^{e\ast }{\mathcal{Q}}(m))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{q^{2}}{2\deg Y}\left(\unicode[STIX]{x1D707}_{HK}({\mathcal{S}})-\unicode[STIX]{x1D707}_{HK}({\mathcal{T}})+\unicode[STIX]{x1D707}_{HK}({\mathcal{Q}})\right)+O(q^{0}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{m\in \mathbb{Z}}\left(h^{0}(F^{e\ast }{\mathcal{S}}(m))-h^{0}(F^{e\ast }{\mathcal{T}}(m))+h^{0}(F^{e\ast }{\mathcal{Q}}(m))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{q^{2}}{2\deg Y}\left(\unicode[STIX]{x1D707}_{HK}({\mathcal{S}})-\unicode[STIX]{x1D707}_{HK}({\mathcal{T}})+\unicode[STIX]{x1D707}_{HK}({\mathcal{Q}})\right)+O(q^{0}).\nonumber\end{eqnarray}$$
(2) If the field is the algebraic closure of a finite field, then the
 $O(q^{0})$
-term is eventually periodic.
$O(q^{0})$
-term is eventually periodic.
The alternating sum in Theorem 2.5 is, in fact, a finite sum for every
![]() $q$
. For
$q$
. For
![]() $m\ll 0$
, the locally free sheaves have no global sections, so all of the terms are
$m\ll 0$
, the locally free sheaves have no global sections, so all of the terms are
![]() $0$
, and for
$0$
, and for
![]() $m\gg 0$
, we have
$m\gg 0$
, we have
![]() $H^{1}(Y,F^{e\ast }{\mathcal{S}}(m))=0$
, and the sum is
$H^{1}(Y,F^{e\ast }{\mathcal{S}}(m))=0$
, and the sum is
![]() $0$
. Moreover, the sum is the dimension of the cokernel
$0$
. Moreover, the sum is the dimension of the cokernel
In [Reference Brenner3], Brenner uses Theorem 2.5 to prove that the Hilbert–Kunz function of a homogeneous
![]() $R_{+}$
-primary ideal
$R_{+}$
-primary ideal
![]() $I$
in a normal two-dimensional standard graded
$I$
in a normal two-dimensional standard graded
![]() $K$
-domain
$K$
-domain
![]() $R$
has the following form:
$R$
has the following form:
where
![]() $e_{HK}(I)$
is a rational number and
$e_{HK}(I)$
is a rational number and
![]() $\unicode[STIX]{x1D6FE}(q)$
is a bounded function, which is eventually periodic if
$\unicode[STIX]{x1D6FE}(q)$
is a bounded function, which is eventually periodic if
![]() $K$
is the algebraic closure of a finite field. In particular, if
$K$
is the algebraic closure of a finite field. In particular, if
![]() $I$
is generated by homogeneous elements
$I$
is generated by homogeneous elements
![]() $f_{1},\ldots ,f_{n}$
of degrees
$f_{1},\ldots ,f_{n}$
of degrees
![]() $d_{1},\ldots ,d_{n}$
, and
$d_{1},\ldots ,d_{n}$
, and
![]() $r_{k}$
,
$r_{k}$
,
![]() $\bar{\unicode[STIX]{x1D707}}_{k}$
denote the numerical invariants of the strong Harder–Narasimhan filtration of the locally free sheaf
$\bar{\unicode[STIX]{x1D707}}_{k}$
denote the numerical invariants of the strong Harder–Narasimhan filtration of the locally free sheaf
![]() $\text{Syz}(f_{1},\ldots ,f_{n})$
on the curve
$\text{Syz}(f_{1},\ldots ,f_{n})$
on the curve
![]() $Y=\text{Proj}R$
, then the Hilbert–Kunz multiplicity of
$Y=\text{Proj}R$
, then the Hilbert–Kunz multiplicity of
![]() $I$
is given by
$I$
is given by
In Section 3, we apply this method to deduce a similar result for the generalized Hilbert–Kunz function, and answer a question of Dao and Smirnov [Reference Dao and Smirnov6, Example 6.2].
3 The generalized Hilbert–Kunz function in dimension
 $2$
$2$
Lemma 3.1. Let
![]() $R$
be a two-dimensional normal
$R$
be a two-dimensional normal
![]() $K$
-domain of positive characteristic
$K$
-domain of positive characteristic
![]() $p$
with homogeneous maximal ideal
$p$
with homogeneous maximal ideal
![]() $\mathfrak{m}$
. We denote by
$\mathfrak{m}$
. We denote by
![]() $U=\text{Spec}R\setminus \{\mathfrak{m}\}$
the punctured spectrum. Let
$U=\text{Spec}R\setminus \{\mathfrak{m}\}$
the punctured spectrum. Let
![]() $M$
be a finitely generated graded
$M$
be a finitely generated graded
![]() $R$
-module with a presentation
$R$
-module with a presentation
Let
![]() $J=I^{\ast \ast }$
be the reflexive hull of
$J=I^{\ast \ast }$
be the reflexive hull of
![]() $I$
(considered inside
$I$
(considered inside
![]() $R^{n}$
), and let
$R^{n}$
), and let
![]() ${\mathcal{L}}$
be the coherent sheaf corresponding to
${\mathcal{L}}$
be the coherent sheaf corresponding to
![]() $J$
on
$J$
on
![]() $U$
, that is,
$U$
, that is,
![]() ${\mathcal{L}}=\widetilde{J}|_{U}$
, then
${\mathcal{L}}=\widetilde{J}|_{U}$
, then
where
![]() $q=p^{e}$
, and
$q=p^{e}$
, and
![]() $\text{im}F^{e\ast }I$
denotes the image of the map
$\text{im}F^{e\ast }I$
denotes the image of the map
![]() $F^{e\ast }I\rightarrow F^{e\ast }R^{n}\cong R^{n}$
.
$F^{e\ast }I\rightarrow F^{e\ast }R^{n}\cong R^{n}$
.
Before proving the lemma, we explain the right-hand side of the equality (3).
First of all, in virtue of (1), we have
![]() $\unicode[STIX]{x1D6E4}(U,F^{e\ast }{\mathcal{L}})=(F^{e\ast }J)^{\ast \ast }$
, so the second equality is clear. Then, the inclusion
$\unicode[STIX]{x1D6E4}(U,F^{e\ast }{\mathcal{L}})=(F^{e\ast }J)^{\ast \ast }$
, so the second equality is clear. Then, the inclusion
![]() $I{\hookrightarrow}R^{n}$
factors through the reflexive module
$I{\hookrightarrow}R^{n}$
factors through the reflexive module
![]() $J$
. Applying the Frobenius functor to these maps, we get a commutative diagram
$J$
. Applying the Frobenius functor to these maps, we get a commutative diagram
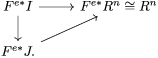
Since the functor
![]() $F^{e\ast }$
is not left exact in general, the maps in (4) are not injective. For this reason, we consider the image
$F^{e\ast }$
is not left exact in general, the maps in (4) are not injective. For this reason, we consider the image
![]() $\text{im}F^{e\ast }I\subseteq R^{n}$
.
$\text{im}F^{e\ast }I\subseteq R^{n}$
.
Since
![]() $R$
is normal,
$R$
is normal,
![]() $U$
is smooth, and the absolute Frobenius morphism
$U$
is smooth, and the absolute Frobenius morphism
![]() $F^{e}:U\rightarrow U$
is exact on
$F^{e}:U\rightarrow U$
is exact on
![]() $U$
. Therefore, we pull back along
$U$
. Therefore, we pull back along
![]() $F^{e}$
the inclusion
$F^{e}$
the inclusion
![]() ${\mathcal{L}}{\hookrightarrow}{\mathcal{O}}_{U}^{n}$
, and we take sections on
${\mathcal{L}}{\hookrightarrow}{\mathcal{O}}_{U}^{n}$
, and we take sections on
![]() $U$
, obtaining the inclusion
$U$
, obtaining the inclusion
Therefore, the quotient
![]() $\unicode[STIX]{x1D6E4}(U,F^{e\ast }{\mathcal{L}})/\text{im}F^{e\ast }I$
is a quotient of submodules of
$\unicode[STIX]{x1D6E4}(U,F^{e\ast }{\mathcal{L}})/\text{im}F^{e\ast }I$
is a quotient of submodules of
![]() $R^{n}$
.
$R^{n}$
.
Proof. We apply the functor
![]() $F^{e\ast }$
to the short exact sequence (2), and we get
$F^{e\ast }$
to the short exact sequence (2), and we get
![]() $F^{e\ast }I\rightarrow R^{n}\rightarrow F^{e\ast }M\rightarrow 0$
. Therefore, we have
$F^{e\ast }I\rightarrow R^{n}\rightarrow F^{e\ast }M\rightarrow 0$
. Therefore, we have
Then, we consider the short exact sequence
Taking local cohomology yields
The module
![]() $\unicode[STIX]{x1D6E4}(U,F^{e\ast }{\mathcal{L}})$
is reflexive by (1), then by Lemma 1.1 the last module of the previous sequence is
$\unicode[STIX]{x1D6E4}(U,F^{e\ast }{\mathcal{L}})$
is reflexive by (1), then by Lemma 1.1 the last module of the previous sequence is
![]() $0$
. Therefore, we get the following isomorphism:
$0$
. Therefore, we get the following isomorphism:
The last equality holds because the module
![]() $\unicode[STIX]{x1D6E4}(U,F^{e\ast }{\mathcal{L}})/\text{im}F^{e\ast }I$
has support in
$\unicode[STIX]{x1D6E4}(U,F^{e\ast }{\mathcal{L}})/\text{im}F^{e\ast }I$
has support in
![]() $\mathfrak{m}$
, since the sheaves
$\mathfrak{m}$
, since the sheaves
![]() ${\mathcal{L}}$
and
${\mathcal{L}}$
and
![]() $\widetilde{I}$
coincide on
$\widetilde{I}$
coincide on
![]() $U$
. Then, the desired formula follows from (5) and (6).◻
$U$
. Then, the desired formula follows from (5) and (6).◻
Theorem 3.2. Let
![]() $R$
be a two-dimensional normal standard graded
$R$
be a two-dimensional normal standard graded
![]() $K$
-domain over an algebraically closed field
$K$
-domain over an algebraically closed field
![]() $K$
of prime characteristic
$K$
of prime characteristic
![]() $p$
, and let
$p$
, and let
![]() $M$
be a finitely generated graded
$M$
be a finitely generated graded
![]() $R$
-module. Then, the generalized Hilbert–Kunz function of
$R$
-module. Then, the generalized Hilbert–Kunz function of
![]() $M$
has the form
$M$
has the form
where
![]() $e_{gHK}(M)$
is a rational number and
$e_{gHK}(M)$
is a rational number and
![]() $\unicode[STIX]{x1D6FE}(q)$
is a bounded function.
$\unicode[STIX]{x1D6FE}(q)$
is a bounded function.
Moreover, if
![]() $K$
is the algebraic closure of a finite field, then
$K$
is the algebraic closure of a finite field, then
![]() $\unicode[STIX]{x1D6FE}(q)$
is an eventually periodic function. In particular, given a graded presentation of
$\unicode[STIX]{x1D6FE}(q)$
is an eventually periodic function. In particular, given a graded presentation of
![]() $M$
$M$
and the corresponding short exact sequence of locally free sheaves on the curve
![]() $Y=\text{Proj}R$
$Y=\text{Proj}R$
then the generalized Hilbert–Kunz multiplicity of
![]() $M$
is
$M$
is
Proof. Let
![]() $u_{1},\ldots ,u_{m}$
be homogeneous generators of
$u_{1},\ldots ,u_{m}$
be homogeneous generators of
![]() $M$
of degrees
$M$
of degrees
![]() $e_{1},\ldots ,e_{m}$
, respectively, and let
$e_{1},\ldots ,e_{m}$
, respectively, and let
be the corresponding short exact sequence. Let
![]() $f_{1},\ldots ,f_{n}$
be homogeneous generators of
$f_{1},\ldots ,f_{n}$
be homogeneous generators of
![]() $I$
of degrees
$I$
of degrees
![]() $d_{1},\ldots ,d_{n}$
respectively and let
$d_{1},\ldots ,d_{n}$
respectively and let
be the corresponding graded short exact sequence. This last sequence induces the short exact sequence (7) on
![]() $Y$
, and the short exact sequence
$Y$
, and the short exact sequence
on the punctured spectrum
![]() $U$
. The modules
$U$
. The modules
![]() $N$
and
$N$
and
![]() $I$
are submodules of finite free
$I$
are submodules of finite free
![]() $R$
-modules, so they are torsion-free. It follows that the corresponding sheaves
$R$
-modules, so they are torsion-free. It follows that the corresponding sheaves
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() $\widetilde{I}|_{U}$
on
$\widetilde{I}|_{U}$
on
![]() $U$
are locally free, since
$U$
are locally free, since
![]() $U$
is regular. Moreover, if
$U$
is regular. Moreover, if
![]() $J=I^{\ast \ast }$
is the reflexive hull of
$J=I^{\ast \ast }$
is the reflexive hull of
![]() $I$
, and
$I$
, and
![]() ${\mathcal{L}}$
is the coherent sheaf corresponding to
${\mathcal{L}}$
is the coherent sheaf corresponding to
![]() $J$
on
$J$
on
![]() $U$
, we have that
$U$
, we have that
![]() ${\mathcal{L}}=\widetilde{I}|_{U}$
as sheaves on
${\mathcal{L}}=\widetilde{I}|_{U}$
as sheaves on
![]() $U$
.
$U$
.
From Lemma 3.1, the generalized Hilbert–Kunz function of
![]() $M$
is given by
$M$
is given by
To compute the last sum, we consider the sequence (7), we pull it back along the
![]() $e\text{th}$
absolute Frobenius morphism on
$e\text{th}$
absolute Frobenius morphism on
![]() $Y$
and we tensor with
$Y$
and we tensor with
![]() ${\mathcal{O}}_{Y}(m)$
, for an integer
${\mathcal{O}}_{Y}(m)$
, for an integer
![]() $m$
. We obtain an exact sequence
$m$
. We obtain an exact sequence
Then, we take global sections
![]() $\unicode[STIX]{x1D6E4}(Y,-)$
of the last sequence and we get
$\unicode[STIX]{x1D6E4}(Y,-)$
of the last sequence and we get
We are interested in the cokernel of the map
![]() $\unicode[STIX]{x1D711}_{m}$
. Its image is clearly
$\unicode[STIX]{x1D711}_{m}$
. Its image is clearly
![]() $(\text{im}F^{e}I)_{m}$
. For the evaluation of the sheaf
$(\text{im}F^{e}I)_{m}$
. For the evaluation of the sheaf
![]() $F^{e\ast }{\mathcal{Q}}(m)$
on
$F^{e\ast }{\mathcal{Q}}(m)$
on
![]() $Y$
, we consider the sequences (7) and (8), and we obtain
$Y$
, we consider the sequences (7) and (8), and we obtain
Therefore, we get
It follows that
We compute the last sum with Theorem 2.5, and we obtain the desired formula for the generalized Hilbert–Kunz function.
For the generalized Hilbert–Kunz multiplicity, it is enough to notice that
![]() $\unicode[STIX]{x1D707}_{HK}({\mathcal{T}})=(\deg Y)^{2}\sum _{i=1}^{n}d_{i}^{2}$
, by Example 2.4.◻
$\unicode[STIX]{x1D707}_{HK}({\mathcal{T}})=(\deg Y)^{2}\sum _{i=1}^{n}d_{i}^{2}$
, by Example 2.4.◻
Corollary 3.3. Let
![]() $I$
be a nonzero ideal generated by homogeneous elements
$I$
be a nonzero ideal generated by homogeneous elements
![]() $f_{1},\ldots ,f_{n}$
of degrees
$f_{1},\ldots ,f_{n}$
of degrees
![]() $d_{1},\ldots ,d_{n}$
, respectively, and let
$d_{1},\ldots ,d_{n}$
, respectively, and let
![]() $d$
be the degree of the ideal sheaf associated to
$d$
be the degree of the ideal sheaf associated to
![]() $I$
on
$I$
on
![]() $Y=\text{Proj}R$
. Then, the generalized Hilbert–Kunz multiplicity of
$Y=\text{Proj}R$
. Then, the generalized Hilbert–Kunz multiplicity of
![]() $R/I$
is given by
$R/I$
is given by
where
![]() $r_{k}$
,
$r_{k}$
,
![]() $\bar{\unicode[STIX]{x1D707}}_{k}$
and
$\bar{\unicode[STIX]{x1D707}}_{k}$
and
![]() $t$
are the numerical invariants of the strong Harder–Narasimhan filtration of the syzygy bundle
$t$
are the numerical invariants of the strong Harder–Narasimhan filtration of the syzygy bundle
![]() $\text{Syz}(f_{1},\ldots ,f_{n})$
.
$\text{Syz}(f_{1},\ldots ,f_{n})$
.
Proof. In this case, the presenting sequence of
![]() $R/I$
is just
$R/I$
is just
![]() $0\rightarrow I\rightarrow R\rightarrow R/I\rightarrow 0$
, and the sequence (7) is then
$0\rightarrow I\rightarrow R\rightarrow R/I\rightarrow 0$
, and the sequence (7) is then
Therefore, by Theorem 3.2, the generalized Hilbert–Kunz multiplicity of
![]() $R/I$
is given by
$R/I$
is given by
In this situation,
![]() ${\mathcal{Q}}$
is a line bundle, so by Example 2.3,
${\mathcal{Q}}$
is a line bundle, so by Example 2.3,
![]() $\unicode[STIX]{x1D707}_{HK}({\mathcal{Q}})=(\deg {\mathcal{Q}})^{2}=d^{2}$
, and by definition,
$\unicode[STIX]{x1D707}_{HK}({\mathcal{Q}})=(\deg {\mathcal{Q}})^{2}=d^{2}$
, and by definition,
![]() $\unicode[STIX]{x1D707}_{HK}(\text{Syz}(f_{1},\ldots ,f_{n}))=\sum _{k=1}^{t}r_{k}\bar{\unicode[STIX]{x1D707}}_{k}^{2}$
.◻
$\unicode[STIX]{x1D707}_{HK}(\text{Syz}(f_{1},\ldots ,f_{n}))=\sum _{k=1}^{t}r_{k}\bar{\unicode[STIX]{x1D707}}_{k}^{2}$
.◻
Example 3.4. Let
![]() $h$
be a homogeneous element of degree
$h$
be a homogeneous element of degree
![]() $a>0$
, and let
$a>0$
, and let
![]() $I=(h)$
. Then, we have
$I=(h)$
. Then, we have
![]() $0\rightarrow {\mathcal{O}}_{Y}(-a)\xrightarrow[{}]{\simeq }{\mathcal{L}}\rightarrow 0$
; hence,
$0\rightarrow {\mathcal{O}}_{Y}(-a)\xrightarrow[{}]{\simeq }{\mathcal{L}}\rightarrow 0$
; hence,
![]() $\text{Syz}(h)=0$
. Since
$\text{Syz}(h)=0$
. Since
![]() $I$
is principal, the degree of the ideal sheaf associated to
$I$
is principal, the degree of the ideal sheaf associated to
![]() $I$
is
$I$
is
![]() $a\cdot \deg Y$
. The generalized Hilbert–Kunz multiplicity is then
$a\cdot \deg Y$
. The generalized Hilbert–Kunz multiplicity is then
in accordance with Proposition 1.2.
Example 3.5. Let
![]() $I$
be a prime ideal of height 1 generated by two homogeneous elements
$I$
be a prime ideal of height 1 generated by two homogeneous elements
![]() $f$
and
$f$
and
![]() $g$
of degrees
$g$
of degrees
![]() $a$
and
$a$
and
![]() $b$
, respectively. Then, the syzygy sequence is
$b$
, respectively. Then, the syzygy sequence is
with
![]() ${\mathcal{Q}}$
the line bundle of, say, degree
${\mathcal{Q}}$
the line bundle of, say, degree
![]() $d$
associated to the ideal
$d$
associated to the ideal
![]() $I$
. From this sequence, we see that the syzygy bundle has rank 1 and degree
$I$
. From this sequence, we see that the syzygy bundle has rank 1 and degree
![]() $\deg Y(-a-b)-d$
. Therefore, we have
$\deg Y(-a-b)-d$
. Therefore, we have
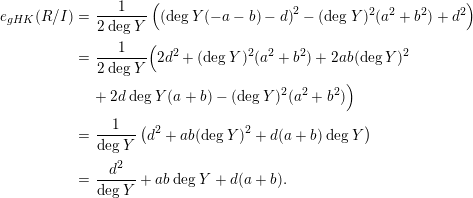 $$\begin{eqnarray}\displaystyle e_{gHK}(R/I) & = & \displaystyle \frac{1}{2\deg Y}\left(\left(\deg Y(-a-b)-d\right)^{2}-(\deg Y)^{2}(a^{2}+b^{2})+d^{2}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\deg Y}\Big(2d^{2}+(\deg Y)^{2}(a^{2}+b^{2})+2ab(\deg Y)^{2}\nonumber\\ \displaystyle & & \displaystyle +\,2d\deg Y(a+b)-(\deg Y)^{2}(a^{2}+b^{2})\Big)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\deg Y}\left(d^{2}+ab(\deg Y)^{2}+d(a+b)\deg Y\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{d^{2}}{\deg Y}+ab\deg Y+d(a+b).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{gHK}(R/I) & = & \displaystyle \frac{1}{2\deg Y}\left(\left(\deg Y(-a-b)-d\right)^{2}-(\deg Y)^{2}(a^{2}+b^{2})+d^{2}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\deg Y}\Big(2d^{2}+(\deg Y)^{2}(a^{2}+b^{2})+2ab(\deg Y)^{2}\nonumber\\ \displaystyle & & \displaystyle +\,2d\deg Y(a+b)-(\deg Y)^{2}(a^{2}+b^{2})\Big)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\deg Y}\left(d^{2}+ab(\deg Y)^{2}+d(a+b)\deg Y\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{d^{2}}{\deg Y}+ab\deg Y+d(a+b).\nonumber\end{eqnarray}$$
Example 3.6. Let
![]() $P$
be a point of the smooth projective curve
$P$
be a point of the smooth projective curve
![]() $Y=\text{Proj}R$
, and let
$Y=\text{Proj}R$
, and let
![]() $I\subseteq R$
be the corresponding homogeneous prime ideal of height 1. The ideal
$I\subseteq R$
be the corresponding homogeneous prime ideal of height 1. The ideal
![]() $I$
is minimally generated by two linear forms
$I$
is minimally generated by two linear forms
![]() $f$
and
$f$
and
![]() $g$
. In fact,
$g$
. In fact,
![]() $f$
and
$f$
and
![]() $g$
correspond to two hyperplanes in the projective space where
$g$
correspond to two hyperplanes in the projective space where
![]() $Y$
is embedded which meet transversally in
$Y$
is embedded which meet transversally in
![]() $P$
. Then, using the notations of Example 3.5, we have
$P$
. Then, using the notations of Example 3.5, we have
![]() $a=b=1$
, and
$a=b=1$
, and
![]() $d=-1$
, since the line bundle
$d=-1$
, since the line bundle
![]() ${\mathcal{Q}}$
associated to the ideal
${\mathcal{Q}}$
associated to the ideal
![]() $I$
is a subsheaf of
$I$
is a subsheaf of
![]() ${\mathcal{O}}_{Y}$
. Therefore, we obtain
${\mathcal{O}}_{Y}$
. Therefore, we obtain
4 The limit of generalized Hilbert–Kunz multiplicity
Let
![]() $R$
be a standard graded domain flat over
$R$
be a standard graded domain flat over
![]() $\mathbb{Z}$
such that almost all fiber rings
$\mathbb{Z}$
such that almost all fiber rings
![]() $R_{p}=R\otimes _{\mathbb{Z}}\mathbb{Z}/p\mathbb{Z}$
are geometrically normal two-dimensional domains. We define
$R_{p}=R\otimes _{\mathbb{Z}}\mathbb{Z}/p\mathbb{Z}$
are geometrically normal two-dimensional domains. We define
![]() $R_{0}:=R\otimes _{\mathbb{Z}}\mathbb{Q}$
and the corresponding projective curve
$R_{0}:=R\otimes _{\mathbb{Z}}\mathbb{Q}$
and the corresponding projective curve
![]() $Y_{0}:=\text{Proj}R_{0}$
over the generic point. We denote by
$Y_{0}:=\text{Proj}R_{0}$
over the generic point. We denote by
![]() $Y_{p}:=\text{Proj}R_{p}$
the projective curve over the prime number
$Y_{p}:=\text{Proj}R_{p}$
the projective curve over the prime number
![]() $p$
. This is a smooth projective curve for almost all primes. If
$p$
. This is a smooth projective curve for almost all primes. If
![]() ${\mathcal{S}}$
is a sheaf over the curve
${\mathcal{S}}$
is a sheaf over the curve
![]() $Y:=\text{Proj}R$
, we denote by
$Y:=\text{Proj}R$
, we denote by
![]() ${\mathcal{S}}_{p}$
(resp.
${\mathcal{S}}_{p}$
(resp.
![]() ${\mathcal{S}}_{0}$
) the corresponding restriction to the curves
${\mathcal{S}}_{0}$
) the corresponding restriction to the curves
![]() $Y_{p}$
(resp.
$Y_{p}$
(resp.
![]() $Y_{0}$
).
$Y_{0}$
).
Remark 4.1. In our setting, the curves
![]() $Y_{0}$
and
$Y_{0}$
and
![]() $Y_{p}$
are not defined over an algebraically closed field. However, we may consider the curves
$Y_{p}$
are not defined over an algebraically closed field. However, we may consider the curves
![]() $\overline{Y}_{0}:=Y_{0}\times _{\mathbb{Q}}\overline{\mathbb{Q}}$
and
$\overline{Y}_{0}:=Y_{0}\times _{\mathbb{Q}}\overline{\mathbb{Q}}$
and
![]() $\overline{Y}_{p}:=Y_{p}\times _{\mathbb{Z}/p\mathbb{Z}}\overline{\mathbb{Z}/p\mathbb{Z}}$
, which are smooth projective curves over the algebraic closures. We can consider the definitions of degree, slope, semistable, HN filtration and strong HN filtration for these curves, and transfer them to the original curves
$\overline{Y}_{p}:=Y_{p}\times _{\mathbb{Z}/p\mathbb{Z}}\overline{\mathbb{Z}/p\mathbb{Z}}$
, which are smooth projective curves over the algebraic closures. We can consider the definitions of degree, slope, semistable, HN filtration and strong HN filtration for these curves, and transfer them to the original curves
![]() $Y_{0}$
and
$Y_{0}$
and
![]() $Y_{p}$
. Therefore, we move to the algebraic closure and back whenever this is convenient.
$Y_{p}$
. Therefore, we move to the algebraic closure and back whenever this is convenient.
Let
![]() $M$
be a graded
$M$
be a graded
![]() $R$
-module. For every prime
$R$
-module. For every prime
![]() $p$
, we can consider the reduction to characteristic
$p$
, we can consider the reduction to characteristic
![]() $p$
,
$p$
,
![]() $M_{p}:=M\otimes _{R}R_{p}\cong M\otimes _{\mathbb{Z}}\mathbb{Z}/p\mathbb{Z}$
, and compute the generalized Hilbert–Kunz multiplicity
$M_{p}:=M\otimes _{R}R_{p}\cong M\otimes _{\mathbb{Z}}\mathbb{Z}/p\mathbb{Z}$
, and compute the generalized Hilbert–Kunz multiplicity
![]() $e_{gHK}^{R_{p}}(M_{p})$
of the
$e_{gHK}^{R_{p}}(M_{p})$
of the
![]() $R_{p}$
-module
$R_{p}$
-module
![]() $M_{p}$
. Since the projective curve
$M_{p}$
. Since the projective curve
![]() $Y_{p}$
is smooth for almost all primes
$Y_{p}$
is smooth for almost all primes
![]() $p$
, by Theorem 3.2, we know that
$p$
, by Theorem 3.2, we know that
![]() $e_{gHK}^{R_{p}}(M_{p})$
exists, and that it is rational for these primes. We are interested in the behavior of
$e_{gHK}^{R_{p}}(M_{p})$
exists, and that it is rational for these primes. We are interested in the behavior of
![]() $e_{gHK}^{R_{p}}(M_{p})$
for
$e_{gHK}^{R_{p}}(M_{p})$
for
![]() $p\rightarrow +\infty$
.
$p\rightarrow +\infty$
.
We introduce the following characteristic zero version of the Hilbert–Kunz slope.
Definition 4.2. Let
![]() ${\mathcal{S}}$
be a locally free sheaf over a projective curve over an algebraically closed field of characteristic zero, and let
${\mathcal{S}}$
be a locally free sheaf over a projective curve over an algebraically closed field of characteristic zero, and let
![]() ${\mathcal{S}}_{1}\subseteq \cdots \subseteq {\mathcal{S}}_{t}={\mathcal{S}}$
be the Harder–Narasimhan filtration of
${\mathcal{S}}_{1}\subseteq \cdots \subseteq {\mathcal{S}}_{t}={\mathcal{S}}$
be the Harder–Narasimhan filtration of
![]() ${\mathcal{S}}$
. For every
${\mathcal{S}}$
. For every
![]() $k=1,\ldots ,t$
, we set
$k=1,\ldots ,t$
, we set
![]() $\bar{\unicode[STIX]{x1D707}}_{k}=\bar{\unicode[STIX]{x1D707}}_{k}({\mathcal{S}})=\unicode[STIX]{x1D707}({\mathcal{S}}_{k}/{\mathcal{S}}_{k-1})$
and
$\bar{\unicode[STIX]{x1D707}}_{k}=\bar{\unicode[STIX]{x1D707}}_{k}({\mathcal{S}})=\unicode[STIX]{x1D707}({\mathcal{S}}_{k}/{\mathcal{S}}_{k-1})$
and
![]() $r_{k}=\text{rank}({\mathcal{S}}_{k}/{\mathcal{S}}_{k-1})$
. The Hilbert–Kunz slope of
$r_{k}=\text{rank}({\mathcal{S}}_{k}/{\mathcal{S}}_{k-1})$
. The Hilbert–Kunz slope of
![]() ${\mathcal{S}}$
is the rational number
${\mathcal{S}}$
is the rational number
The name Hilbert–Kunz slope is justified by the following result of Trivedi (cf. [Reference Trivedi12, Lemma 1.14]).
Lemma 4.3. (Trivedi)
Let
![]() $h\in \mathbb{Z}_{+}$
, let
$h\in \mathbb{Z}_{+}$
, let
![]() $Y$
be a smooth projective curve over
$Y$
be a smooth projective curve over
![]() $\text{Spec}\mathbb{Z}_{h}$
, and let
$\text{Spec}\mathbb{Z}_{h}$
, and let
![]() ${\mathcal{S}}$
be a locally free sheaf over
${\mathcal{S}}$
be a locally free sheaf over
![]() $Y$
. We denote by
$Y$
. We denote by
![]() ${\mathcal{S}}_{0}$
and
${\mathcal{S}}_{0}$
and
![]() ${\mathcal{S}}_{p}$
the restrictions of
${\mathcal{S}}_{p}$
the restrictions of
![]() ${\mathcal{S}}$
to
${\mathcal{S}}$
to
![]() $Y_{0}$
and
$Y_{0}$
and
![]() $Y_{p}$
, for
$Y_{p}$
, for
![]() $p\nmid h$
. Then,
$p\nmid h$
. Then,
Theorem 4.4. Let
![]() $R$
be a standard graded domain flat over
$R$
be a standard graded domain flat over
![]() $\mathbb{Z}$
such that almost all fiber rings
$\mathbb{Z}$
such that almost all fiber rings
![]() $R_{p}=R\otimes _{\mathbb{Z}}\mathbb{Z}/p\mathbb{Z}$
are geometrically normal two-dimensional domains. Let
$R_{p}=R\otimes _{\mathbb{Z}}\mathbb{Z}/p\mathbb{Z}$
are geometrically normal two-dimensional domains. Let
![]() $M$
be a graded
$M$
be a graded
![]() $R$
-module with a graded presentation
$R$
-module with a graded presentation
and corresponding short exact sequence of locally free sheaves
![]() $0\rightarrow {\mathcal{S}}_{0}\rightarrow {\mathcal{T}}_{0}\rightarrow {\mathcal{Q}}_{0}\rightarrow 0$
on the generic fiber
$0\rightarrow {\mathcal{S}}_{0}\rightarrow {\mathcal{T}}_{0}\rightarrow {\mathcal{Q}}_{0}\rightarrow 0$
on the generic fiber
![]() $Y_{0}=\text{Proj}R_{0}$
, with notations as above. Then, the limit
$Y_{0}=\text{Proj}R_{0}$
, with notations as above. Then, the limit
exists, and it is equal to the rational number
Proof. Let
![]() $u_{1},\ldots ,u_{m}$
be homogeneous generators of
$u_{1},\ldots ,u_{m}$
be homogeneous generators of
![]() $M$
as
$M$
as
![]() $R$
-module, and let
$R$
-module, and let
![]() $f_{1},\ldots ,f_{n}$
be homogeneous generators of
$f_{1},\ldots ,f_{n}$
be homogeneous generators of
![]() $I:=\text{Syz}(u_{1},\ldots ,u_{m})$
. We obtain two short exact sequences
$I:=\text{Syz}(u_{1},\ldots ,u_{m})$
. We obtain two short exact sequences
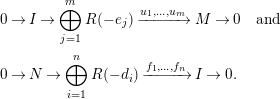 $$\begin{eqnarray}\displaystyle & & \displaystyle 0\rightarrow I\rightarrow \bigoplus _{j=1}^{m}R(-e_{j})\xrightarrow[{}]{u_{1},\ldots ,u_{m}}M\rightarrow 0\quad \text{and}\nonumber\\ \displaystyle & & \displaystyle 0\rightarrow N\rightarrow \bigoplus _{i=1}^{n}R(-d_{i})\xrightarrow[{}]{f_{1},\ldots ,f_{n}}I\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 0\rightarrow I\rightarrow \bigoplus _{j=1}^{m}R(-e_{j})\xrightarrow[{}]{u_{1},\ldots ,u_{m}}M\rightarrow 0\quad \text{and}\nonumber\\ \displaystyle & & \displaystyle 0\rightarrow N\rightarrow \bigoplus _{i=1}^{n}R(-d_{i})\xrightarrow[{}]{f_{1},\ldots ,f_{n}}I\rightarrow 0.\end{eqnarray}$$
Tensoring these sequences with the flat
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
![]() $\mathbb{Q}$
, we obtain exact sequences of
$\mathbb{Q}$
, we obtain exact sequences of
![]() $R_{0}$
-modules. On the other hand, if we apply the functor
$R_{0}$
-modules. On the other hand, if we apply the functor
![]() $-\otimes _{\mathbb{Z}}\mathbb{Z}/p\mathbb{Z}$
to the sequences (9), exactness is preserved for all primes except for a finite number of them. Let
$-\otimes _{\mathbb{Z}}\mathbb{Z}/p\mathbb{Z}$
to the sequences (9), exactness is preserved for all primes except for a finite number of them. Let
![]() $h$
be the product of those primes, and we consider the smooth projective curve
$h$
be the product of those primes, and we consider the smooth projective curve
![]() $Y=\text{Proj}R_{h}$
over
$Y=\text{Proj}R_{h}$
over
![]() $\text{Spec}\mathbb{Z}_{h}$
.
$\text{Spec}\mathbb{Z}_{h}$
.
Let
![]() $U=D(R_{h+})$
denote the relative punctured spectrum. The sheaf
$U=D(R_{h+})$
denote the relative punctured spectrum. The sheaf
![]() $\widetilde{I}|_{U}$
restricts to
$\widetilde{I}|_{U}$
restricts to
![]() $U_{0}=U\cap \text{Spec}R_{0}$
as a locally free sheaf. By possibly shrinking the set
$U_{0}=U\cap \text{Spec}R_{0}$
as a locally free sheaf. By possibly shrinking the set
![]() $D(h)$
, we may assume that
$D(h)$
, we may assume that
![]() $\widetilde{I}|_{U}$
is locally free. By further shrinking, we may assume that
$\widetilde{I}|_{U}$
is locally free. By further shrinking, we may assume that
![]() ${\mathcal{E}}:=\widetilde{N}|_{U}$
is also locally free. Then, for almost all
${\mathcal{E}}:=\widetilde{N}|_{U}$
is also locally free. Then, for almost all
![]() $p$
,
$p$
,
![]() $I_{p}$
and
$I_{p}$
and
![]() $N_{p}$
are locally free on
$N_{p}$
are locally free on
![]() $U_{p}$
.
$U_{p}$
.
Let
![]() ${\mathcal{S}}$
,
${\mathcal{S}}$
,
![]() ${\mathcal{T}}$
,
${\mathcal{T}}$
,
![]() ${\mathcal{Q}}$
be the locally free sheaves on
${\mathcal{Q}}$
be the locally free sheaves on
![]() $Y$
corresponding to
$Y$
corresponding to
![]() ${\mathcal{E}}$
,
${\mathcal{E}}$
,
![]() $\bigoplus _{i=1}^{n}R(-d_{i})$
,
$\bigoplus _{i=1}^{n}R(-d_{i})$
,
![]() $\widetilde{I}|_{U}$
, which, by the second sequence of (9), form an exact sequence
$\widetilde{I}|_{U}$
, which, by the second sequence of (9), form an exact sequence
![]() $0\rightarrow {\mathcal{S}}\rightarrow {\mathcal{T}}\rightarrow {\mathcal{Q}}\rightarrow 0$
on
$0\rightarrow {\mathcal{S}}\rightarrow {\mathcal{T}}\rightarrow {\mathcal{Q}}\rightarrow 0$
on
![]() $Y$
. Its restrictions give the short exact sequences
$Y$
. Its restrictions give the short exact sequences
![]() $0\rightarrow {\mathcal{S}}_{0}\rightarrow {\mathcal{T}}_{0}\rightarrow {\mathcal{Q}}_{0}\rightarrow 0$
on the generic fiber
$0\rightarrow {\mathcal{S}}_{0}\rightarrow {\mathcal{T}}_{0}\rightarrow {\mathcal{Q}}_{0}\rightarrow 0$
on the generic fiber
![]() $Y_{0}$
, and
$Y_{0}$
, and
![]() $0\rightarrow {\mathcal{S}}_{p}\rightarrow {\mathcal{T}}_{p}\rightarrow {\mathcal{Q}}_{p}\rightarrow 0$
on the fiber
$0\rightarrow {\mathcal{S}}_{p}\rightarrow {\mathcal{T}}_{p}\rightarrow {\mathcal{Q}}_{p}\rightarrow 0$
on the fiber
![]() $Y_{p}$
, for
$Y_{p}$
, for
![]() $p\nmid h$
.
$p\nmid h$
.
Let
![]() $p$
be a prime number not dividing
$p$
be a prime number not dividing
![]() $h$
, then we are in the situation of Theorem 3.2, so we obtain
$h$
, then we are in the situation of Theorem 3.2, so we obtain
Then, taking the limit for
![]() $p\rightarrow +\infty$
and applying Lemma 4.3, we conclude the proof.◻
$p\rightarrow +\infty$
and applying Lemma 4.3, we conclude the proof.◻
Acknowledgments
We would like to thank Mohsen Asgharzadeh for a careful reading of an earlier version of this article, and Hailong Dao for many helpful conversations. We thank the referee for showing us how to simplify the proofs of Lemma 1.1 and Lemma 1.3. Moreover, we thank the DFG Graduiertenkolleg Kombinatorische Strukturen in der Geometrie at Osnabrück for support.