Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Von Christian, Ulrich
1982.
Bemerkungen zu einer Arbeit von B. Diehl.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 52,
Issue. 1,
p.
160.
Christian, Ulrich
1983.
On the analytic continuation of Eisenstein series for Siegel's modular group of degreen.
Monatshefte f�r Mathematik,
Vol. 96,
Issue. 2,
p.
101.
Sato, Fumihiro
1998.
Eisenstein series on weakly spherical homogeneous spaces of ${\rm GL}(n)$.
Tohoku Mathematical Journal,
Vol. 50,
Issue. 1,
Katsurada, Masanori
2015.
Complete asymptotic expansions associated with Epstein zeta-functions II.
The Ramanujan Journal,
Vol. 36,
Issue. 3,
p.
403.
Terras, Audrey
2016.
Harmonic Analysis on Symmetric Spaces—Higher Rank Spaces, Positive Definite Matrix Space and Generalizations.
p.
1.


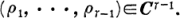 Define
Define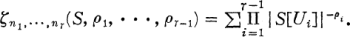
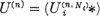 which lie in a complete set of representatives for the equivalence relation
which lie in a complete set of representatives for the equivalence relation 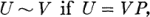 with
with