Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-11T09:58:58.933Z Has data issue: false hasContentIssue false
  • English
  • Français

FUJITA DECOMPOSITION AND MASSEY PRODUCT FOR FIBERED VARIETIES

Part of: Surfaces and higher-dimensional varieties Deformations of analytic structures Families, fibrations Cycles and subschemes

Published online by Cambridge University Press:  29 November 2021

LUCA RIZZI Open the ORCID record for LUCA RIZZI [Opens in a new window]  and
FRANCESCO ZUCCONI Open the ORCID record for FRANCESCO ZUCCONI [Opens in a new window]
LUCA RIZZI
Affiliation:
Graduate School of Mathematical Sciences University of Tokyo Tokyo 153-8914, Japan [email protected]
FRANCESCO ZUCCONI
Affiliation:
Department of Mathematics, Computer Science and Physics Università di Udine Udine 33100, Italy [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 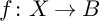$f\colon X\to B$ be a semistable fibration where X is a smooth variety of dimension 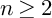$n\geq 2$ and B is a smooth curve. We give the structure theorem for the local system of the relative 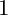$1$ -forms and of the relative top forms. This gives a neat interpretation of the second Fujita decomposition of 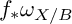$f_*\omega _{X/B}$ . We apply our interpretation to show the existence, up to base change, of higher irrational pencils and on the finiteness of the associated monodromy representations under natural Castelnuovo-type hypothesis on local subsystems. Finally, we give a criterion to have that X is not of Albanese general type if 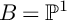$B=\mathbb {P}^1$ .

MSC classification

Primary: 14D06: Fibrations, degenerations
Secondary: 14C30: Transcendental methods, Hodge theory , Hodge conjecture 14J40: $n$-folds ($n>4$) 32G20: Period matrices, variation of Hodge structure; degenerations
Type
Article
Information
Nagoya Mathematical Journal , Volume 247 , September 2022 , pp. 624 - 652
Check for updates
Copyright
© (2021) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Luca Rizzi is supported by the Japan Society for the Promotion of Science, Postdoctoral Fellowship for Research in Japan. Francesco Zucconi is supported by the project “Progetti di Ricerca di Rilevante Interesse Nazionale, Geometric Analytic and Algebraic Aspects of Arithmetic.”

References

Barja, M. Á., González-Alonso, V., and Naranjo, J. C., Xiao’s conjecture for general fibred surfaces, J. Reine Angew. Math. 739 (2018), 297–308.CrossRefGoogle Scholar
Catanese, F., Moduli and classification of irregular Kaehler manifolds (and algebraic varieties) with Albanese general type fibrations, Invent. Math. 104 (1991), 263–289.CrossRefGoogle Scholar
Catanese, F. and Dettweiler, M., The direct image of the relative dualizing sheaf needs not be semiample, C. R. Math. Acad. Sci. Paris 352 (2014), 241–244.Google Scholar
Catanese, F. and Dettweiler, M., Vector bundles on curves coming from variation of Hodge structures, Internat. J. Math. 27 (2016), art. ID 1640001, 25 p.Google Scholar
Catanese, F. and Dettweiler, M., “Answer to a question by Fujita on variation of Hodge structures” in Higher Dimensional Algebraic Geometry: In Honour of Professor Yujiro Kawamata’s Sixtieth Birthday, Math. Soc. Japan, Tokyo, 2017, 73–102.CrossRefGoogle Scholar
Catanese, F. and Kawamata, Y., Fujita decomposition over higher dimensional base, Eur. J. Math. 5 (2019), 720–728.CrossRefGoogle Scholar
Cattani, E., El Zein, F., Griffiths, P. A., and Tráng, L. D., eds., Hodge Theory, Math. Notes 49, Princeton Univ. Press, Princeton, 2014.Google Scholar
Cesarano, L., Rizzi, L., and Zucconi, F., On birationally trivial families and adjoint quadrics, preprint, arXiv:1903.06307 Google Scholar
Collino, A., Naranjo, J. C., and Pirola, G. P., The Fano normal function, J. Math. Pures Appl. (9) 98 (2012), 346–366.Google Scholar
Collino, A. and Pirola, G. P., The Griffiths infinitesimal invariant for a curve in its Jacobian, Duke Math. J. 78 (1995), 59–88.Google Scholar
Deligne, P., Equations Différentielles à Points Siunguliers Réguliers, Lecture Notes in Math. 163, Springer, Berlin–Heidelberg–New York, 1970.CrossRefGoogle Scholar
Fujita, T., On Kähler fiber spaces over curves, J. Math. Soc. Japan 30 (1978), 779–794.CrossRefGoogle Scholar
Fujita, T., The sheaf of relative canonical forms of a Kähler fiber space over a curve, Proc. Japan Acad. Ser. A Math. Sci. 54 (1978), 183–184.CrossRefGoogle Scholar
González-Alonso, V., On deformations of curves supported on rigid divisors, Ann. Mat. Pura Appl. (4) 195 (2016), 111–132.Google Scholar
González-Alonso, V., Stoppino, L., and Torelli, S., On the rank of the flat unitary summand of the Hodge bundle, Trans. Amer. Math. Soc. 372 (2019), 8663–8677.Google Scholar
González-Alonso, V. and Torelli, S., Families of curves with Higgs field of arbitrarily large kernel, Bull. London Math. Soc. 53 (2021) Issue 2, 493–506.CrossRefGoogle Scholar
Illusie, L., Réduction semi-stable et décomposition de complexes de de Rham à coefficients, Duke Math. J. 60 (1990), 139–185.CrossRefGoogle Scholar
Kobayashi, S. and Ochiai, T., Meromorphic mappings onto compact complex spaces of general type, Invent. Math. 31 (1976), 7–16.CrossRefGoogle Scholar
Konno, K., On the irregularity of special non-canonical surfaces, Publ. Res. Inst. Math. Sci. 30 (1994), 671–688.CrossRefGoogle Scholar
Maillot, V. and Rössler, D., Une conjecture sur la torsion des classes de Chern des fibrés de Gauss–Manin, Publ. Res. Inst. Math. Sci. 46 (2010), 789–828.Google Scholar
Mori, S., Classification of higher-dimensional varieties, Proc. Sympos. Pure Math. 46 (1987), 269–332.CrossRefGoogle Scholar
Pareschi, G. and Popa, M., Strong generic vanishing and a higher-dimensional Castelnuovo-de Franchis inequality, Duke Math. J. 150 (2009), 269–285.CrossRefGoogle Scholar
Peters, C. A. M. and Steenbrink, J. H. M., Mixed Hodge Structures, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics 52, Springer, Berlin, 2008.Google Scholar
Pirola, G. P. and Rizzi, C., Infinitesimal invariant and vector bundles, Nagoya Math. J. 186 (2007), 95–118.CrossRefGoogle Scholar
Pirola, G. P. and Torelli, S., Massey products and Fujita decompositions on fibrations of curves, Collect. Math. 71 (2020), 39–61.CrossRefGoogle Scholar
Pirola, G. P. and Zucconi, F., Variations of the Albanese morphisms, J. Algebraic Geom. 12 (2003), 535–572.CrossRefGoogle Scholar
Ran, Z., On subvarieties of abelian varieties, Invent. Math. 62 (1981), 459–479.CrossRefGoogle Scholar
Raviolo, E., Some geometric applications of the theory of variations of Hodge structures, Ph.D. dissertation.Google Scholar
Rizzi, L., On Massey products and rational homogeneous varieties, preprint, arXiv:2012.06375 Google Scholar
Rizzi, L. and Zucconi, F., Generalized adjoint forms on algebraic varieties, Ann. Mat. Pura Appl. (4) 196 (2017), 819–836.CrossRefGoogle Scholar
Rizzi, L. and Zucconi, F., On Green’s proof of infinitesimal Torelli theorem for hypersurfaces. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 29 (2018), 689–709.CrossRefGoogle Scholar
Rizzi, L. and Zucconi, F., Differential forms and quadrics of the canonical image, Ann. Mat. Pura Appl. (4) 199 (2020), 2341–2356.CrossRefGoogle Scholar
Ueno, K., Classification Theory of Algebraic Varieties and Compact Complex Spaces, Lecture Notes in Math. 439, Springer, Berlin–Heidelberg, 1975.CrossRefGoogle Scholar
Voisin, C., Hodge Theory and Complex Algebraic Geometry, I. Cambridge Stud. Adv. Math. 76, Cambridge Univ. Press, Cambridge, 2002, translated from the French by Leila Schneps.CrossRefGoogle Scholar
Voisin, C., Hodge Theory and Complex Algebraic Geometry, II, Cambridge Stud. Adv. Math. 77, Cambridge Univ. Press, Cambridge, 2003, translated from the French by Leila Schneps.Google Scholar
Xiao, G., Algebraic surfaces with high canonical degree, Math. Ann. 274 (1986), 473–483.Google Scholar