In our previous paper [3] we proved the following ([3, Theorem 16]) :

THEOREM A. Let G be a 2-group of class 3. Let G2 and G/G2 be direct products of cyclic groups 〈yq〉 of order αq (1 ≦ q ≦ m), and of cyclic groups 〈hi〉 of order βi (1 ≦ i ≦ n) with β1 ≧ β2 ≧ · · · βn, respectively. Let xi be representatives of hi (1 ≦ i ≦ n), and put 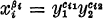Then a homomorphism ψ:G3→T can be extended to a polynomial map from G to T of degree ≦ 4 if and only if there exists an integral solution in the following linear equations of Xiq (1 ≦ i ≦ n, 1 ≦ q ≦ m) with coefficients in T:

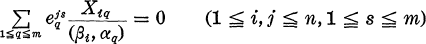(I)

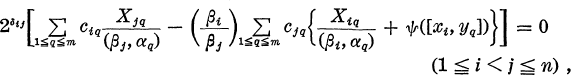
where δij is the Kronecker symbol for βi: i.e. δij = 1 or 0 according to βi = βj or βi > βj, respectively.