Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T08:08:01.093Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite Dimensional Approximations to Some Flows on the Projective Limit Space of Spheres

Published online by Cambridge University Press:  22 January 2016

Hisao Nomoto
Hisao Nomoto*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Ω be the projective limit space of a sequence of probability space Ωn which is a certain subset of (n − 1)-dimensional sphere with the usual uniform probability distribution on it. T. Hida [2], starting from a sequence of finite dimensional flows 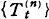which are derived from some one-parameter subgroups of rotations of spheres, constructed a flow {Tt} on Ω as the limit of them. Observing his method, the concept of consistency of flows 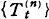which approximate {Tt} seems to play an essential role in his work [2]. As will be made clear in the following sections, the concept of consistency is closely related to the projective limiting structure of our basic space Ω. The purpose of this paper is to determine all the flows on Ω which can be approximated in the sense of [2] by finite dimensional flows.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 28 , October 1966 , pp. 167 - 177
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1966

References

[1] Bochner, S., Harmonic Analysis and the Theory of Probability, Uni. of Calf. Press, 1955.CrossRefGoogle Scholar
[2] Hida, T., Finite dimensional approximations to White noise and Brownian motion., J. Math. Mech., (to appear).Google Scholar
[3] Hida, T. and Nomoto, H., Gaussian Measure on the Projective Limit Space of Spheres., Proc. Japan Acad., 40 (1964), 301–304.Google Scholar
[4] Levy, P., Problems concrets d’analyse fonctionelle, Gauthier-Villars, 1951.Google Scholar
[5] Totoki, H., Flow and Entropy, Seminar on Prob., 20 (1964), 1–130 (Japanese).Google Scholar