Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T15:07:34.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Filtrage approche et calcul stochastique non causal

Published online by Cambridge University Press:  22 January 2016

Monique Pontier
Monique Pontier*
Affiliation:
Département “Mathématiques & Informatique”, Université d’Orléans, B. P. 6759, 45067, Orléans Cedex 2, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

On considère un signal X partiellement observé par un processus vectoriel Y, où la mesure H du signal dépend de l’observation:

(1.1) .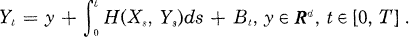

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 118 , June 1990 , pp. 1 - 33
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1990

References

[1] Dellacherie, C. - Meyer, P., “Probabilités et Potentiels”, T 1 & 2, Hermann, Paris, 1980.Google Scholar
[2] Masi, G. B. Di - Pratelli, M. - Runggaldier, W. J., “An approximation for the nonlinear filtering problem with error bound”, Stochastics, 15 (1985), 247–271.CrossRefGoogle Scholar
[3] Ikeda, N. - Watanabe, S., “Stochastic Differential Equations and Diffusion Process”, North Holland, Amsterdam, 1981.Google Scholar
[4] Ikeda, N. - Watanabe, S., “Malliavin calculus of Wiener functionals and its applications”, Warwick Symposium on “Stochastic Differential Equations and Applications”, From local times to global geometry, control and physics, edited by Elworthy, K. D., Pitman Research Notes in Math. Series 150, Longman Scientific and Technical, New York, 1986.Google Scholar
[5] Korezlioglu, H. - Mazziotto, G., “Modélisation et filtrage de systèmes stochastiques non linéaires” Note technique CNET, 1983.Google Scholar
[6] Millet, A. - Nualart, D. - Sanz, M., “Integration by parts and time reversal for diffusion processes”, Preprint, 1987.Google Scholar
[7] Nualart, D., “Non causal stochastic integral and calculus”, Workshop on Stochastic Analysis, Silivri (Istanbul), July 1986, L.N. in Maths n°1316, Springer-Verlag, New York, 1988.Google Scholar
[8] Nualart, D. - Zakai, M., “Generalized stochastic integrals and the Malliavin calculus”, Probab. Theory, 73 (1986), 255–280.Google Scholar
[9] Pardoux, E. - Protter, P., “Two sided-stochastic Integrals”, Probab. Theory, 76–1 (1987), 15–50.Google Scholar
[10] Picard, J., “An estimate of the error in time discretization of nonlinear filtering problems”, 7th MT NS Symposium, Stockholm, 1985.Google Scholar
[11] Pontier, M., “Approximation d’un filtre avec observation sur une variété compacte”, Stochastics, 24 (1988), 285–304.Google Scholar
[12] Sugita, H., “On a characterization of Sobolev Spaces over an abstract Wiener space”, J. Math. Kyoto Univ., 25 (1985), 717–725.Google Scholar
[13] Ustunel, A. S., “The Itô formula for anticipative processes with non monotonous time scale via the Malliavin calculus”, Theory of Probability and related fields, 79 (1988), 249–269.Google Scholar
[13b] Ustunel, A. S. “Representation of the distributions on Wiener Space and Stochastic Calculus of Variations”, J. of Funct. Anal., 70 (1987), 126–139.Google Scholar
[14] Watanabe, S., “Stochastic Differential Equation and Malliavin calculus”, Tata Institute of Fundamental Research, Bombay, 1984.Google Scholar
[15] Zakai, M., “The Malliavin calculus”, Acta Appl. Math., 3 (1985), 175–207.Google Scholar
[16] Taniguchi, S., “Malliavin’s Stochastic calculus of Variations for Manifold-Valued Wiener Functionals and its Applications”, Z. Wahrsch., 65 (1983), 269–290.Google Scholar
[17] Davis, M. H. A., “The Wiener space derivative for functionals of diffusions on manifolds”, Nonlinearity, 1, United Kingdom, 1988, 241–251.Google Scholar