Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Opolka, Hans
1986.
Zur darstellungstheoretischen Deutung von Kohomologiegruppen.
Archiv der Mathematik,
Vol. 46,
Issue. 2,
p.
136.
1989.
Topics in Field Theory.
Vol. 155,
Issue. ,
p.
477.
1993.
Continuation of the Notas de Matemàtica.
Vol. 177,
Issue. ,
p.
831.
Opolka, Hans
1996.
The lifting problem in group cohomology.
Journal of Pure and Applied Algebra,
Vol. 107,
Issue. 2-3,
p.
263.


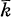 be an algebraic closure of
be an algebraic closure of 