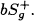Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cho, Sanghyun
2002.
Embedding of pseudoconvex CR manifolds of Levi-forms with one degenerate eigenvalue.
Pacific Journal of Mathematics,
Vol. 207,
Issue. 2,
p.
311.
Cho, Sanghyun
2003.
Extension of CR structures on pseudoconvex CR manifolds with one degenerate eigenvalue.
Tohoku Mathematical Journal,
Vol. 55,
Issue. 3,
Cho, Sanghyun
2022.
Extension of CR structures on pseudoconvex CR-manifolds with comparable eigenvalues of the Levi-form.
Complex Variables and Elliptic Equations,
Vol. 67,
Issue. 10,
p.
2319.


 be a smoothly bounded orientable pseudoconvex
be a smoothly bounded orientable pseudoconvex  which is the concave side of
which is the concave side of