Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berglund, Nils
Fernandez, Bastien
and
Gentz, Barbara
2007.
Metastability in interacting nonlinear stochastic differential equations: I. From weak coupling to synchronization.
Nonlinearity,
Vol. 20,
Issue. 11,
p.
2551.
Berglund, Nils
Fernandez, Bastien
and
Gentz, Barbara
2007.
Metastability in interacting nonlinear stochastic differential equations: II. Large-Nbehaviour.
Nonlinearity,
Vol. 20,
Issue. 11,
p.
2583.
Borisov, D.
and
Sultanov, O.
2020.
Asymptotic analysis of mean exit time for dynamical systems with a single well potential.
Journal of Differential Equations,
Vol. 269,
Issue. 8,
p.
78.
Borisov, Denis I.
and
Sultanov, Oskar A.
2020.
Complete Asymptotics for Solution of Singularly Perturbed Dynamical Systems with Single Well Potential.
Mathematics,
Vol. 8,
Issue. 6,
p.
949.
Nectoux, Boris
2021.
Mean exit time for the overdamped Langevin process: the case with critical points on the boundary.
Communications in Partial Differential Equations,
Vol. 46,
Issue. 9,
p.
1789.
2022.
Correction.
Communications in Partial Differential Equations,
Vol. 47,
Issue. 7,
p.
1536.


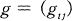 and let
and let 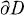 and a compact closure
and a compact closure 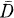 . Suppose that
. Suppose that 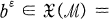
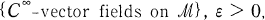 are given and that
are given and that 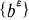 converges uniformly to
converges uniformly to 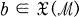 on
on 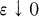 for some neighborhood
for some neighborhood 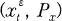 on
on 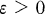 generated by
generated by