Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T23:35:01.567Z Has data issue: false hasContentIssue false
  • English
  • Français

Evans-Kuramochi Exhaustion Functions on Non-Algebroid Riemann Surfaces

Published online by Cambridge University Press:  22 January 2016

J.E. Skeath
J.E. Skeath*
Affiliation:
Swarthmore College, Swarthmore, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 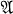denote a non-compact parabolic Riemann surface, and let 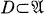be compact and such that each frontier point of D is contained in a continuum that is also contained in D.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 39 , August 1970 , pp. 157 - 166
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1970

References

[1] Heins, M., Riemann surfaces of infinite genus, Ann. of Math., vol. 55 (1952), pp. 296–317.CrossRefGoogle Scholar
[2] Kuramochi, Z., Evans* theorem on abstract Riemann surfaces with null boundaries. I and II., Proc. Japan Acad. vol. 32 (1956), pp. 1–6 and 7–9.Google Scholar
[3] Nakai, M., On Evans potential, Proc. Japan Acad., vol. 38 (1962), pp. 624–629.Google Scholar
[4] Skeath, E., An extension of the Denjoy-Carleman-Ahlfors theorem in subharmonic form, Trans. Amer. Math. Soc., vol. 119 (1965), pp. 535–551.Google Scholar