Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tsuji, Hajime
2010.
Dynamical construction of Kähler-Einstein metrics.
Nagoya Mathematical Journal,
Vol. 199,
Issue. ,
p.
107.
Berman, Robert J.
Boucksom, Sébastien
Guedj, Vincent
and
Zeriahi, Ahmed
2013.
A variational approach to complex Monge-Ampère equations.
Publications mathématiques de l'IHÉS,
Vol. 117,
Issue. 1,
p.
179.
Tsuji, Hajime
2015.
Complex Analysis and Geometry.
Vol. 144,
Issue. ,
p.
327.
Choi, Young-Jun
2015.
Variations of Kähler–Einstein metrics on strongly pseudoconvex domains.
Mathematische Annalen,
Vol. 362,
Issue. 1-2,
p.
121.
Guenancia, Henri
2020.
Families of conic Kähler–Einstein metrics.
Mathematische Annalen,
Vol. 376,
Issue. 1-2,
p.
1.
Cao, Junyan
Guenancia, Henri
and
Păun, Mihai
2021.
Variation of singular Kähler–Einstein metrics: Positive Kodaira dimension.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2021,
Issue. 779,
p.
1.
Deleporte, Alix
2021.
Toeplitz Operators with Analytic Symbols.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 4,
p.
3915.
IOOS, Louis
2022.
Anticanonically balanced metrics on Fano manifolds.
Annals of Global Analysis and Geometry,
Vol. 62,
Issue. 1,
p.
1.
Reboulet, Rémi
2023.
The space of finite-energy metrics over a degeneration of complex manifolds.
Journal de l’École polytechnique — Mathématiques,
Vol. 10,
Issue. ,
p.
659.
Tsuji, Hajime
2024.
The Bergman Kernel and Related Topics.
Vol. 447,
Issue. ,
p.
321.
Yoo, Sungmin
2025.
Invariant Weighted Bergman Metrics on Domains.
The Journal of Geometric Analysis,
Vol. 35,
Issue. 2,


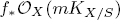 with semipositive curvature in the sense of Nakano.
with semipositive curvature in the sense of Nakano.