Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beauville, A.
1983.
Algebraic Geometry.
Vol. 1016,
Issue. ,
p.
238.
Mehta, V B
and
Nori, M V
1984.
Semistable sheaves on homogeneous spaces and abelian varieties.
Proceedings Mathematical Sciences,
Vol. 93,
Issue. 1,
p.
1.
Schenk, H.
1988.
On a generalised Fourier transform of instantons over flat tori.
Communications in Mathematical Physics,
Vol. 116,
Issue. 2,
p.
177.
Braam, Peter J.
and
van Baal, Pierre
1989.
Nahm's transformation for instantons.
Communications in Mathematical Physics,
Vol. 122,
Issue. 2,
p.
267.
Brambila Paz, L.
1989.
Algebraic Geometry and Complex Analysis.
Vol. 1414,
Issue. ,
p.
15.
Kronheimer, Peter B.
and
Nakajima, Hiraku
1990.
Yang-Mills instantons on ALE gravitational instantons.
Mathematische Annalen,
Vol. 288,
Issue. 1,
p.
263.
Nakayashiki, Atsushi
1991.
Structure of Baker-Akhiezer modules of principally polarized abelian varieties, commuting partial differential operators and associated integrable systems.
Duke Mathematical Journal,
Vol. 62,
Issue. 2,
Braam, Peter J.
Maciocia, Antony
and
Todorov, Andrey
1992.
Instanton moduli as a novel map from tori to K3-surfaces.
Inventiones Mathematicae,
Vol. 108,
Issue. 1,
p.
419.
Ballico, Edoardo
1993.
Complex Analysis and Geometry.
p.
387.
Bartocci, C.
Bruzzo, U.
and
Ruipérez, D. Hernández
1994.
Fourier-Mukai transform and index theory.
Manuscripta Mathematica,
Vol. 85,
Issue. 1,
p.
141.
Maciocia, Antony
1994.
The determinant line bundle over moduli spaces of instantons on abelian surfaces.
Mathematische Zeitschrift,
Vol. 217,
Issue. 1,
p.
317.
Künnemann, Klaus
1994.
Arakelov Chow groups of abelian schemes, arithmetic Fourier transform, and analogues of the standard conjectures of Lefschetz type.
Mathematische Annalen,
Vol. 300,
Issue. 1,
p.
365.
Kimura, Shun-Ichi
1994.
Correspondences to abelian varieties I.
Duke Mathematical Journal,
Vol. 73,
Issue. 3,
Rothstein, Mitchell
1996.
Connections on the total Picard sheaf and the KP hierarchy.
Acta Applicandae Mathematicae,
Vol. 42,
Issue. 3,
p.
297.
Kimura, Shun-ichi
and
Vistoli, Angelo
1996.
Chow rings of infinite symmetric products.
Duke Mathematical Journal,
Vol. 85,
Issue. 2,
Bruzzo, Ugo
and
Maciocia, Antony
1996.
Hilbert schemes of points on some K3 surfaces and Gieseker stable bundles.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 120,
Issue. 2,
p.
255.
Rothstein, Mitchell
1996.
Sheaves with connection on abelian varieties.
Duke Mathematical Journal,
Vol. 84,
Issue. 3,
Park, Jae-Suk
1997.
Monads and D-instantons.
Nuclear Physics B,
Vol. 493,
Issue. 1-2,
p.
198.
Orlov, D. O.
1997.
Equivalences of derived categories andK3 surfaces.
Journal of Mathematical Sciences,
Vol. 84,
Issue. 5,
p.
1361.
Ein, Lawrence
and
Lazarsfeld, Robert
1997.
Singularities of theta divisors and the birational geometry of irregular varieties.
Journal of the American Mathematical Society,
Vol. 10,
Issue. 1,
p.
243.


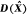 with its application to picard sheaves
with its application to picard sheaves