Published online by Cambridge University Press: 22 January 2016
It is a well-known result due to Sjogren [9] that if G is a finitely generated p-group then, for all n ≦ − 1, the (n + 2)-th dimension sub-group Dn+2(G) of G coincides with γn+2(G), the (n + 2)-th term of the lower central series of G. This was earlier proved by Moran [5] for n ≦ p − 2. For p = 2, Sjogren’s result is the best possible as Rips [8] has exhibited a finite 2-group G for which D4G) ≠ γ4(G) (see also Tahara [10, 11]). In this note we prove that if G is a finitely generated metabelian p-group then, for all 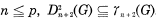 . It follows, in particular, that, for p odd,
. It follows, in particular, that, for p odd, 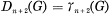 for all n ≦ p and all metabelian p-groups G.
for all n ≦ p and all metabelian p-groups G.