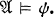Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Taylor, Walter
1973.
A heterogeneous interpolant.
Nagoya Mathematical Journal,
Vol. 52,
Issue. ,
p.
31.
Espíndola, Christian
2025.
Completeness of Infinitary Heterogeneous Logic.
Notre Dame Journal of Formal Logic,
Vol. 66,
Issue. 1,


 in
in  in
in