Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T23:37:12.540Z Has data issue: false hasContentIssue false
  • English
  • Français

DETECTING KOSZULNESS AND RELATED HOMOLOGICAL PROPERTIES FROM THE ALGEBRA STRUCTURE OF KOSZUL HOMOLOGY

Part of: Rings and algebras arising under various constructions Commutative algebra: Homological methods

Published online by Cambridge University Press:  18 June 2018

AMANDA CROLL ,
ROGER DELLACA ,
ANJAN GUPTA ,
JUSTIN HOFFMEIER ,
VIVEK MUKUNDAN ,
LIANA M. ŞEGA ,
GABRIEL SOSA ,
PEDER THOMPSON  and
DENISE RANGEL TRACY
AMANDA CROLL
Affiliation:
Concordia University Irvine, Irvine, CA 92612, USA email [email protected]
ROGER DELLACA
Affiliation:
Department of Mathematics, University of California–Irvine, Irvine, CA 92697, USA email [email protected]
ANJAN GUPTA
Affiliation:
Dipartimento di Matematica, Università degli studi di Genova, Via Dodecaneso 35, 16146 Genova, Italy email [email protected]
JUSTIN HOFFMEIER
Affiliation:
Department of Mathematics & Statistics, Northwest Missouri State University, Maryville, MO 64468, USA email [email protected]
VIVEK MUKUNDAN
Affiliation:
Purdue University & School of Mathematics, Tata Institute of Fundamental Research, Mumbai, India email [email protected]
LIANA M. ŞEGA
Affiliation:
Department of Mathematics and Statistics, University of Missouri, Kansas City, MO 64110, USA email [email protected]
GABRIEL SOSA
Affiliation:
Department of Mathematics and Statistics, Amherst College, Amherst, MA 01002, USA email [email protected]
PEDER THOMPSON
Affiliation:
Department of Mathematics and Statistics, Texas Tech University, Lubbock, TX 79409, USA email [email protected]
DENISE RANGEL TRACY
Affiliation:
Department of Mathematics, Central Connecticut State University, New Britain, CT 06050, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

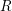Let $k$ be a field and $R$ a standard graded 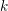$k$-algebra. We denote by 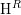$\operatorname{H}^{R}$ the homology algebra of the Koszul complex on a minimal set of generators of the irrelevant ideal of 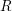$R$. We discuss the relationship between the multiplicative structure of 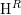$\operatorname{H}^{R}$ and the property that 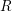$R$ is a Koszul algebra. More generally, we work in the setting of local rings and we show that certain conditions on the multiplicative structure of Koszul homology imply strong homological properties, such as existence of certain Golod homomorphisms, leading to explicit computations of Poincaré series. As an application, we show that the Poincaré series of all finitely generated modules over a stretched Cohen–Macaulay local ring are rational, sharing a common denominator.

MSC classification

Primary: 13D07: Homological functors on modules (Tor, Ext, etc.) 13D02: Syzygies, resolutions, complexes 16S37: Quadratic and Koszul algebras
Type
Article
Information
Nagoya Mathematical Journal , Volume 238 , June 2020 , pp. 47 - 85
Copyright
© 2018 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This material is based upon work supported by the National Science Foundation under Grant #1321794, as part of the Mathematical Research Communities 2015 program in Snowbird, Utah, and by a grant from the Simons Foundation (#354594, Liana Şega). Anjan Gupta was supported by the Istituto Nazionale di Alta Matematica “Francesco Severi” fellowship.

References

Avramov, L. L., Small homomorphisms of local rings, J. Algebra 50(2) (1978), 400–453.Google Scholar
Avramov, L. L., “Golod homomorphisms”, in Algebra, Algebraic Topology and Their Interactions (Stockholm, 1983), Lecture Notes in Math. 1183, Springer, Berlin, 1986, 59–78.Google Scholar
Avramov, L. L., “Infinite free resolutions”, in Six Lectures on Commutative Algebra (Bellaterra, 1996), Progr. Math. 166, Birkhäuser, Basel, 1998, 1–118.Google Scholar
Avramov, L. L., Conca, A. and Iyengar, S. B., Subadditivity of syzygies of Koszul algebras, Math. Ann. 361(1–2) (2015), 511–534.10.1007/s00208-014-1060-4Google Scholar
Avramov, L. L., Iyengar, S. B. and Şega, L. M., Free resolutions over short local rings, J. Lond. Math. Soc. (2) 78(2) (2008), 459–476.10.1112/jlms/jdn027Google Scholar
Avramov, L. L., Kustin, A. R. and Miller, M., Poincaré series of modules over local rings of small embedding codepth or small linking number, J. Algebra 118(1) (1988), 162–204.10.1016/0021-8693(88)90056-7Google Scholar
Boocher, A., D’Alì, A., Grifo, E., Montaño, J. and Sammartano, A., Edge ideals and DG algebra resolutions, Matematiche (Catania) 70(1) (2015), 215–238.Google Scholar
Dress, A. and Krämer, H., Bettireihen von Faserprodukten lokaler Ringe, Math. Ann. 215 (1975), 79–82.Google Scholar
Ghione, F. and Gulliksen, T. H., Some reduction formulas for the Poincaré series of modules, Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. (8) 58(2) (1975), 82–91.Google Scholar
Golod, E. S., On the homologies of certain local rings, Sov. Math. Dokl. 3 (1962), 745–748.Google Scholar
Grayson, D. R. and Stillman, M. E., Macaulay2, a software system for research in algebraic geometry. Available at http://www.math.uiuc.edu/Macaulay2/, 2016.Google Scholar
Herzog, J. and Iyengar, S. B., Koszul modules, J. Pure Appl. Algebra 201(1–3) (2005), 154–188.Google Scholar
Hoffmeier, J. and Şega, L. M., Conditions for the Yoneda algebra of a local ring to be generated in low degrees, J. Pure Appl. Algebra 221(2) (2017), 304–315.10.1016/j.jpaa.2016.06.010Google Scholar
Iyengar, S. B. and Römer, T., Linearity defects of modules over commutative rings, J. Algebra 322(9) (2009), 3212–3237.Google Scholar
Kustin, A. R., Şega, L. M. and Vraciu, A., Poincaré series of compressed local Artinian rings with odd top socle degree, J. Algebra 505 (2018), 383–419.10.1016/j.jalgebra.2018.02.034Google Scholar
Lescot, J., “La série de Bass d’un produit fibré d’anneaux locaux”, in Paul Dubreil and Marie-Paule Malliavin algebra seminar, 35th year (Paris, 1982), Lecture Notes in Math. 1029, Springer, Berlin, 1983, 218–239.Google Scholar
Levin, G. L., Poincaré series of modules over local rings, Proc. Amer. Math. Soc. 72(1) (1978), 6–10.Google Scholar
Levin, G. L. and Avramov, L. L., Factoring out the socle of a Gorenstein ring, J. Algebra 55(1) (1978), 74–83.10.1016/0021-8693(78)90191-6Google Scholar
Löfwall, C., “On the subalgebra generated by the one-dimensional elements in the Yoneda Ext-algebra”, in Algebra, Algebraic Topology and Their Interactions (Stockholm, 1983), Lecture Notes in Math. 1183, Springer, Berlin, 1986, 291–338.10.1007/BFb0075468Google Scholar
May, J. P., Matric Massey products, J. Algebra 12 (1969.), 533–568.10.1016/0021-8693(69)90027-1Google Scholar
Moore, W. F., Cohomology over fiber products of local rings, J. Algebra 321(3) (2009), 758–773.10.1016/j.jalgebra.2008.10.015Google Scholar
Roos., J.-E., “Relations between Poincaré-Betti series of loop spaces and of local rings”, in Séminaire d’Algèbre Paul Dubreil 31ème année (Paris, 1977–1978), Lecture Notes in Math. 740, Springer, Berlin, 1979, 285–322.Google Scholar
Roos, J.-E., Homological properties of the homology algebra of the Koszul complex of a local ring: examples and questions, J. Algebra 465 (2016), 399–436.10.1016/j.jalgebra.2016.06.033Google Scholar
Rossi, M. E. and Şega, L. M., Poincaré series of modules over compressed Gorenstein local rings, Adv. Math. 259 (2014), 421–447.Google Scholar
Sally, J. D., The Poincaré series of stretched Cohen–Macaulay rings, Canad. J. Math. 32(5) (1980), 1261–1265.10.4153/CJM-1980-094-0Google Scholar
Şega, L. M., Homological properties of powers of the maximal ideal of a local ring, J. Algebra 241(2) (2001), 827–858.10.1006/jabr.2001.8786Google Scholar